在動手操作中學數學

劉林源

《數學課程標準》指出：“有效的數學學習活動不能單純地依賴模仿與記憶，動手實踐、自主探索與合作交流是學習數學的重要方式. ”可見，動手操作是小學數學課堂教學中一種重要的教學活動形式. 教師應從學生的生活經驗和已有的知識背景出發，為學生提供充分進行數學實踐活動的機會，調動學生參與數學學習活動，使學生親身感知體驗數學知識的形成過程.

一、在動手操作中學習新知

建構主義教學論認為：學生的知識建構不是教師傳授與輸出的結果，而是通過親歷，通過與學習環境間的交互作用來實現的. 事實上，真正能培養學生創新精神與實踐能力的活動，必須是學生的自主活動.

三年級上冊數學廣角——搭配. 兩件上裝和三件下裝搭配有幾種不同的穿法？先讓學生利用學具動手擺一擺，學生已從生活中得到一些經驗，但還不會有序地思考問題. 通過動手擺一擺，會產生一些思考：怎樣擺才能又快又完整地擺出所有的搭配？對于參差不齊的學生，有學生在擺過程中找到了方法，有的學生則沒有，因此學生在匯報時，出現以下四種情況：1.沒有順序的擺，得到有6種不同的搭配；2.沒有順序的擺，結果是少于6種或多于6種的搭配；3.有序的擺，先確定上裝，再搭配下裝；4.先確定下裝，再搭配上裝，這也是有序的擺. 不管怎樣，學生動手操作，已幫助他們建立了表象，從中獲取了經驗，再從學生的匯報中優化方法，無疑是后面兩種方法比較好. 通過動手操作，經歷探索的過程，找到解決問題的正確方法，學生對新知的理解會更加深刻.

二、在動手操作中深入理解

教學分數的初步認識——認識幾分之一時，通過例題的教學學生認識了二分之一，顯然，學生二分之一的代表的意義是不夠深刻的，于是接著讓學生動手折一折、涂一涂表示出紙片的二分之一.

部分學生作品：

通過折紙片這個動手操作的教學環節，不但調動了學生的積極性，使學生熱情的參與到學習中來，符合了學生的年齡特點和認知水平，而且學生在動手操作的過程中也提升了他們的思維. “他們圖形不一樣，折法也不一樣，怎么都表示出了它們圖形的二分之一呢？對比一下它們有什么共同的特征？”使學生深刻理解 “平均分”，分數中“2”和“1”各表示什么意義，也就認識了二分之一代表的意義. 學生不僅親身經歷了知識產生過程、體驗了愉快的學習過程，也只有這樣引導學生有效學習，才能有利于學生學習更有價值的數學.

三、在動手操作中解決問題

小學生的思維是直觀形象思維逐漸過度到抽象邏輯思維. 要解決純粹的抽象邏輯思維問題，對他們來說還是很困難的，必須多組織學生動手操作，以“動”啟發學生的思維，讓他們“動”中進一步深化自己的想法，在“動”中找題中的數量關系，在“動”中尋求解決問題的方法.

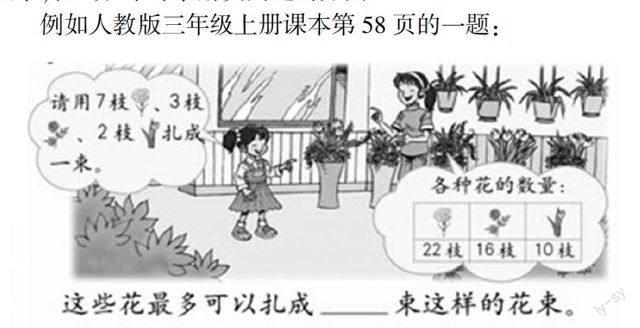
例如人教版三年級上冊課本第58頁的一題：

這是一道思維性較強的綜合題，有一定難度. 學生通常做法有：1. 22 + 16 + 10 = 48（枝），7 + 3 + 2 = 12（枝），48 ÷ 12 = 4（束）；2. 22 ÷ 7 = 3（束）……1（枝），16 ÷ 3 = 5（束）……1（枝），10 ÷ 2 = 5（束），3 + 5 + 5 = 13（束）.

從上面兩種錯誤解答來看，學生除了沒有正確理解題意外，思維方式也是錯的. 雖然這類情況在生活中很常見，但對于三年級的學生來說還是很少接觸，他們動手“分花”的機會少，所以做錯也就不足為怪. 針對學生的“思維困境”，在教學中我用動手操作這一策略，分別用圓形、三角形和長方形紙片代替康乃馨、玫瑰和郁金香，讓學生在小組內動手操作分一分，通過實際操作，他們很快得出結論，扎成3束后康乃馨已不夠7枝，不能再分了，所以最多可以扎成3束. 然后通過整理用算式表示出來.

動手操作，不僅促使學生深入理解題意，清晰地理解和掌握題中的數量關系，而且啟發了學生的思維，是解決問題簡單有效的方法.

著名心理學家皮亞杰說：“兒童的思維是從動作開始的，切斷動作與思維的關系，思維就不能得到發展. ”動手操作最能體現教學的直觀性原則，它有助于把抽象的知識形象化、具體化. 在操作中學習，讓學生成為學習的主人，幫助他們在自主探索的過程中理解和掌握基本的數學知識與技能、數學思想和方法，獲得廣泛的數學活動經驗，并促使學生的動手實踐能力、思維能力和創新精神方面得到發展.