物流運輸中多車型配送車輛的調度模型

潘新元　崔艷　鐘秋平

【摘要】多車型多路徑的單個配送中心的車輛調度優化是城市配送中的典型問題.針對該問題，本文從空駛成本、運輸成本兩個維度構建了一個VRP的數學模型，并采用爬山算法對模型加以求解.通過實例仿真，獲得其最低運輸成本的方案.

【關鍵詞】車輛調度；物流配送；多車型

【中圖分類號】U492.2 【文獻標識碼】A

配送車輛調度問題是運籌學和組合優化領域的熱點問題.多車型配送車輛調度問題是配送車輛調度問題的一個分支，一般情況下，配送企業為了適應配送商品種類繁多、性質各異、客戶要求各不相同的情況，往往配置多種類型的配送車輛，以提高車輛的滿載率，降低配送成本.可見，研究多車型配送車輛調度問題具有重要的理論和現實意義.

本文在現有研究成果的基礎上，建立了多車型配送車輛調度問題的基于直觀描述的數學模型，考慮的目標函數和約束條件比較接近實際，決策變量、目標函數和約束條件的表示較為自然、直觀和易于理解.

1.對多車型配送車輛調度問題的描述

現實中的多車型配送車輛調度問題十分復雜，為了方便建模和求解，需要對現實問題進行一些抽象和簡化.現對本文研究的多車型配送車輛調度問題作如下描述：

1）從一個配送中心向多個客戶送貨，配送中心供應的貨物能夠滿足所有客戶的需求；

2）各個客戶需求的貨物均可以混裝，單一客戶的貨物需求量不超過配送車輛的最大載重量，每個客戶的送貨要求必須滿足，且僅能由一輛車完成，不允許分批配送；

3）配送車輛按載重量分類，每種車型的最大載重量一定且不允許超載，每種車型

的一次配送最大行駛距離一定，不允許超過.配送車輛均由配送中心出發，向一些客戶提供配送服務，最后返回配送中心；

4）配送中心與客戶之間及客戶相互之間的最短距離已知且固定.

在滿足上述條件下，我們要求運輸成本最小.

2.構建數學模型

現有一個有向圖G=（V，E），其中V={0，1，…，N}有N+1個頂點，E={（i，j）|i，j∈V，i≠j}表示弧集，頂點0表示配送中心，剩余的頂點集V′=V＼{0}表示N個配送點，為構建多車型最小費用車輛路徑問題數學模型，定義以下參數：

gi： 配送點i的需求量；

φ={1，2，…，L}為車輛類型的集合，類型總數為L；

Kl：l車型的數量；

φl：車型l的車輛數集，φl={1，2，…，Kl}；

dij： 兩個節點間的最短距離，i，j∈V；

Ql： 車型l的裝載能力，Q0l表示車型l的空重；

cl： l型車每公里每噸的載重費用，單位：元/噸·公里；

clkij： l型車的第k輛從第i點到第j點的費用，與距離和載重有關：

clkij=dijclrlkij（i，j）∈E；l∈φ；k∈φl；

rlkij： l型車的第k輛從第i點到第j點車輛的重量；

xlkij=1 l型車的第k輛從第i點行駛到第j點0 否則

式（1）表示目標函數，即總配送成本最小；

式（2）保證車輛都是從配送中心出發，最后回到配送中心；

式（3）表示進入每個貨物需求點的車輛卸載后會離開；

式（4）、（5）確保每個貨物需求點只能被一輛車服務一次；

式（6）表示車輛承載的貨物量之和不得大于車輛的容量；

式（7）是遞推車輛行駛路徑的總車質量；

式（8）是車輛回到配送中心時車輛的重量；

式（9）是不超過車輛的裝載能力；

式（10）是經過某一配送點時車輛重量不能小于空車重量；

式（11）是l型車的第k輛從第i點到第j點的費用計算公式.

3.算法過程

在多車型低耗車輛路徑問題解決過程中，本文采用爬山算法作為求解的主要算法.爬山算法是一種局部擇優的方法，它采用啟發式方法，是對深度優先搜索的一種改進，它利用反饋信息幫助生成解的決策.該算法每次從當前解的臨近解空間中選擇一個最優解作為當前解，直到達到一個局部最優解.屬于人工智能算法的一種.爬山算法結構比較簡單，在某些情況下，整體效率還是很好的.但它的主要缺點是有時會陷入局部最優解，而不一定能搜索到全局最優解.但由于它求解時可以把復雜問題簡單化，且解的結果與最優解比較接近，所以在很多領域中都有著廣泛的應用.

爬山算法的基本步驟如下：

第一步：輸入多車型低耗車輛路徑問題，包括配送中心、顧客點之間的坐標，配送

點需求，車型參數（載重能力、空重、不同車型固定成本）等.任意選定一個初始解x0，記錄當前最優解為xbest，且令xbest=x0，令U（xbest）代表xbest的鄰域.

第二步：從xbest的鄰域U（xbest）中按照某一規則選出一個解xnow，轉到第三步；

若當U（xbest）=φ時，或滿足其他停止運算的規則時，轉到第四步；

第三步：計算xnow的目標函數值minZ1，若xnow的目標函數值minZ1小于xbest的目標函數值minZ，則xbest=xnow，minZ=minZ1，U=U（xbest），轉到第二步；否則 U=U-xnow，轉到第二步；

第四步：輸出計算結果，停止.

在爬山算法中，第一步的初始解可以采用隨機方法產生，也可以用一些經驗方法或者采用其他算法得到初始解.第二步中在U（xbest）中選取xnow的規則也可以采用隨機選取的規則.

4.實驗計算和結果分析

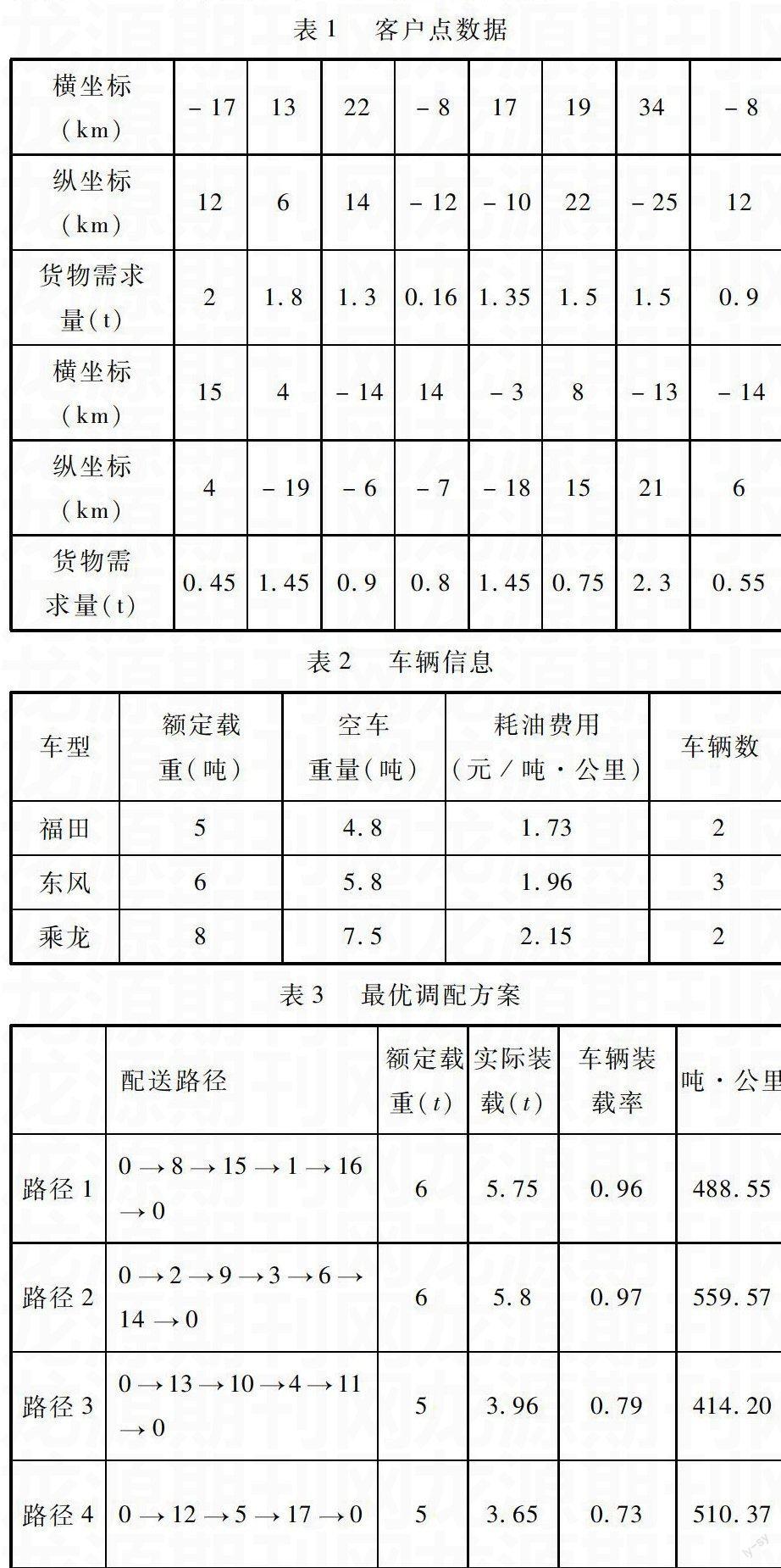
實例：設配送中心（0，0）和16 個客戶配送點分布及需求情況，具體數據見表1，假設該配送中心有3種車型，見表2.根據以上的爬山算法，我們應用Lingo語言來求解，獲得費用最少的行駛路徑，見表3，此時費用為3654.40元.

5.結 論

總的來說，對于復雜的VRP，如果僅憑決策者的經驗，是很難在較短時間內作出一個合理的運輸路徑規劃的，本文利用優化模型，采用爬山算法，再通過Lingo自動搜索得到費用最少的最優路徑和車輛調度數.最終結果是比較令人滿意的.

【參考文獻】

[1]楊浩雄，胡靜，何明珂.配送中多車場多任務多車型車輛調度研究[J].計算機工程與應用，2013，49（10）.

[2]錢艷婷，王鵬濤，魏國利.動態車輛路徑問題的算法研究[J].天津理工大學學報，2010，26（6）.

[3]郭海湘，楊娟，等.煤礦物資多車型配送的改進遺傳算法求解[J].運籌與管理，2011，20（2）.