線性代數：從幾何中抽象

梅麗

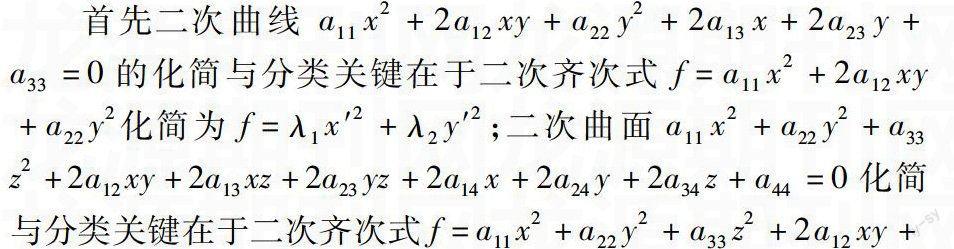
【摘要】對目前流行的國內線性代數教材的主要內容進行了分析，指出其明確的幾何意義，通過幾何直觀和形象思維討論其抽象思維過程，借助其幾何意義可以幫助理解其抽象性，從而更好掌握其內容，對線性代數教學具有一定指導意義.

【關鍵詞】線性代數；幾何；抽象思維

線性代數是研究線性空間和線性變換的一門學科，其核心內容包括矩陣以及向量空間理論，這些概念和理論不僅為各個專業領域提出相關問題時提供了準確的數學表達語言，而且也為解決問題準備了有力的工具.線性代數的主要內容有矩陣與線性方程組、矩陣代數、向量與向量空間、行列式、線性變換、歐氏空間等.現在，它的一些成果已經被廣泛應用到了概率統計、微分方程、離散數學等數學學科，并對這些學科的發展起到了積極的推動作用.它是大學階段理工科、經濟、管理等學科有關專業的重要數學基礎課之一，對提高學生思維品質以及分析問題和解決問題的能力都有很大幫助.但由于課程本身高度的抽象性和邏輯性，很多學生掌握不好，有的同學即使上課聽懂了，但是做起作業來又感到特別困難，從而影響了對后續數學課程甚至專業課程的學習.究其原因，在于學生對線性代數中的基本概念、結論等掌握得不準確，而抽象性是學生學習線性代數的障礙和困難所在.

抽象性是線性代數的一大特點，正是其抽象性決定了其應用的廣泛性.線性代數的教材中到處可見抽象定義，這是由線性代數這門學科本身的特點決定了的.抽象本身并非壞事，“一切科學的抽象，都更深刻、更正確，更完全地反映著自然”（列寧語），在線性代數教學中我們要培養學生的抽象思維能力，卻要克服這種抽象帶來的困難，使學生消除對線性代數的抽象感、陌生感和恐懼感，從而激活其求知欲，增強學好、用好線性代數的信心.

形象思維與抽象思維是思維過程中兩個不同質的階段，它們是辯證統一的.數學的抽象離不開形象直觀，線性代數正是這樣，雖然抽象，卻有非常明確的幾何意義，借助其直觀意義可以幫助理解其抽象性，從而更好掌握其內容，下面以幾個例子加以說明.

一、行列式的概念

行列式是線性代數中的重要內容之一，它在線性代數中有很多應用，因此，學好行列式是非常重要的.但是大多數教材中，介紹行列式概念時采用了比較抽象的定義方式.對此，很多學生只會機械記憶、死記硬背而不能理解其意義，以至于對n階行列式的概念感到無所適從.事實上，一般教科書中都首先介紹了二階和三階行列式作為過渡，但在給出一般n階行列式定義時仍然比較抽象，這時可以繼續以四階行列式作為過渡，將四階行列式作為具體例子詳細討論其定義然后再過渡到一般n階行列式定義，實踐證明效果較好.

為了加深對n階行列式含義的理解，還可以從幾何意義上加以抽象.對于二階行列式D2=a11 a12a21 a22就是以向量α1=（a11，a12），α2=（a21，a22）為邊的平行四邊形的有向面積；當平行四邊形是由α1沿逆時針方向轉到α2形成時，面積為正；而當平行四邊形是由α1沿順時針方向轉到α2形成時，面積為負.同樣三階行列式的值就是三個向量α1，α2，α3在空間形成的平行六面體的體積，當α1，α2，α3構成右手系時，體積為正；而當α1，α2，α3構成左手系時，體積為負.這樣不難得到n階行列式的幾何意義（n個n維向量構成的平行多面體的有向體積）.

二、n 維向量空間

線性代數的中心課題是向量空間，n維向量空間中向量之間的關系特別是線性相關性一直是該課程的難點.要使學生理解一般n維向量空間，可以以一維、二維、三維幾何空間為實例模型.一、二、三維空間是線性代數n 維空間的特例，可以將一、二、三維空間中的點（向量）推廣到四維乃至一般的n維向量空間中的點（向量），一般一、二、三維空間中的線性運算推廣到一般的n維向量空間.由于n維向量空間中的向量有無限，因而有必要討論向量之間的關系，可以分為四類，即向量與向量之間的關系，向量與向量組之間的關系，向量組與向量組之間的關系，向量組內向量之間的關系，它們是一、二、三維空間中向量共線、共面關系的推廣.

三、 線性方程組解的理論

在二、三維空間中的線性方程表示的是直線或平面，一般n維向量空間中的線性方程可以表示n維向量空間中的超平面，由三維空間中平面的相交情況可以推出三元一次方程組解的情況，將之推廣，可得一般n維向量空間中n個未知量的線性方程組解的情況.對于一般的線性方程組可能有解可能無解，無解對應的是這些超平面沒有公共交點，有解對應的是這些超平面至少有一個交點，交點可以唯一、成一直線（或一超平面），從而得到線性方程組解的結構.這樣做，會達到使學生對兩種數學結構（一個是線性代數結構，一個是空間解析幾何關系結構） 的認識互相聯系，互相增強.

四、二次型

將二、三維空間中的直線或平面推廣到一般n維向量空間中的超平面以后，接下來的問題是將二維空間中的二次曲線與三維空間中的二次曲面推廣到一般n維向量空間中的超二次曲面

2a13xz+2a23yz的化簡與分類.一般n維向量空間中超二次曲面的形狀（圖形性質）自然就由n個變量的二次齊次式 f（x1，x2，…，xn）=∑ni=1∑nj=1aijxixj 確定，它就是一個n元二次型（n維向量空間中的超二次曲面）.與二維空間中的曲線、三維空間中的曲面研究類似，欲知n維向量空間中的超二次曲面的形狀，就必須對二次型化簡，化二次型所用的變換一般為射影變換，它改變了曲線的形狀，只有在所用的變換為正交變換時才不改變曲線的形狀.講完二次型的理論之后，自然應該回過頭來用二次型的理論研究一般曲線或曲面的化簡與分類問題.

五、 矩陣與線性變換

二維空間中旋轉變換 x′=cosθx+sinθyy′=-sinθx+cosθy 可以用矩陣表示為

x′y′= cosθ[]sinθ-sinθ[]cosθxy，x′y′=a[]00[]dxy表示二維空間中相似變換，

x′y′=-1[]0 0[]1xy或x′y′=1[]00[]-1xy都表示二維空間中的對稱變換，而

x′y′=a[]bc[]dxy表示二維空間中一般變換.n維向量空間中的一般變換自然就可以表示為X′=AX，其中變換的性質（分類）取決于矩陣A的性質，一個矩陣是一個線性變換在選定基底下的表示，兩個矩陣A，B 相似，就是同一線性變換在兩組不同基下兩種表示之間的關系.正交矩陣、對角矩陣、對稱矩陣分別是二維空間中相應變換的抽象.

六、內積空間

將二維、三維空間抽象到一般內積空間，得到一般向量的長度、向量的夾角、標準正交基等概念，就有了正交變換并可以用以研究二次型.

需要指出的是，線性代數雖然是普通幾何內容的抽象，但是并沒有將所有的幾何內容都抽象到線性代數里來，所以還有很多內容值得學生去探究，比如一般內積空間中點到超平面（曲面）的距離、外積混合積等等.

數學的抽象和其他事物一樣，是在逐漸的不顯著的量變的積累過程中，經過一系列階段而產生、形成和發展起來的，學生在學習的過程中，抽象思維能力的形成和發展也不例外，它是通過對數學知識、技能的理解和逐步掌握而形成發展的，教師要善于引導，從形象思維逐步過渡到抽象思維.

【參考文獻】

[1]同濟大學應用數學系.線性代數（第四版）[M].北京：高等教育出版社，2003.

[2]馬莉，吳翠芳.改進線性代數教學的幾點思考[J].數學學習與研究，2013（1）.

[3]游宏.關于修訂線性代數與空間解析幾何課程教學基本要求的幾點思考[J]. 大學數學， 2004（5）.

[4]王穎.將解析幾何融入線性代數教學中的思考[J].高師理科學刊，2013（4）.

[5]杜建衛， 蘇欣.讓線性代數課程易教易學[J].大學數學，2011（5）.

[6]李尚志.讓抽象變得顯然——建設國家精品課程的體會[J].中國大學教學，2006（7）.

[7]劉學詠.理科線性代數教學的認識與實踐[J].湖北經濟學院學報（人文社會科學版），2006（4）.

[8]毛寶安，楊策，隋文斌.在線性代數教學中應注意學生數學品質的培養[J].現代教育科學，2008（S1）.