常微分方程模型在物體冷卻問題中的應用

高云天

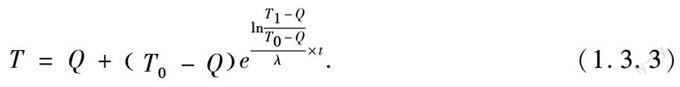
【摘要】常微分方程在諸多領域中都有著重要的應用，本文主要研究在物體冷卻問題中建立常微分方程的數學模型，培養學生建立數學模型的思想，從而更便捷的解決相應問題.

【關鍵詞】常微分方程;物體冷卻;數學模型

1.物體冷卻問題中常微分方程的數學模型

1.1常微分方程的定義

常微分方程是聯系自變量和未知函數以及未知量函數的導數或微分的等式，其中未知函數的導數或微分形式必須出現在方程等式中，而且未知函數只受到一個自變量的變化而變化，則該方程稱為常微分方程.

常微分方程中待定函數最高階導數的階數成為該方程的階，n階常微分方程的一般形式為：F（x，y，y′，y″…，y^（n））=0或y^（n）=F（x，y，y′，y″，…，y（^n-1））.

1.2牛頓冷卻定律

牛頓冷卻定律 溫度高于周圍環境的物體向周圍媒質傳遞熱量逐漸冷卻時所遵循的規律.當物體表面與周圍存在溫度差時，單位時間從單位面積散失的熱量與溫度差成正比.

推論2.1.1 溫度高于周圍環境的物體，它自身的溫度變化率與物體自身溫度和當時周圍溫度的差成正比.

1.3模型的建立

假設一個物體的溫度為T，周圍環境溫度為Q（假設環境溫度一直保持不變），比例常數為λ，t為時間.

分析：物體的溫度的變化率為未知函數溫度T對自變量時間t的一階導數，即為dTdt，在根據推論1.1.1可以列出常微分方程，即得到物體溫度變化率的模型：

dTdt=-λ（T-Q）

（1.3.1）

對上式方程進行分離變量[2]：

dTdt=-λ（T-Q）dTT-Q=-λdt.

對上式方程兩邊同時求積分：

∫dTT-Q=∫ λdtlnT-Q=-λt+C.

（C為任意常數）

elnT-Q=e-λt+c±（T-Q）=e-λt+cT-Q=±e-λt+cT-Q=±ece-λtT-Q=Ke-λt.

（K=±ec，為常數）

整理可以得到物體溫度T隨時間t變化的數學模型：

T=Q+Ke-λt（K=±ec，為常數）.

（1.3.2）

設物體的初始溫度為T0，當t1時刻的物體溫度為T1的時候有：

T0=Q+Ke-λ×0K=T0-Q，

T1=Q+Ke-λt1T1=Q+（T0-Q）e-λt1

T1-QT0-Q=e-λt1lnT1-QT0-Q=lne-λt1-λt1=lnT1-QT0-Qt1=-lnT1-QT0-Qλ.

從而將模型（1.3.2）變為：

T=Q+T0-QelnT1-QT0-Qλ×t.

（1.3.3）

此模型說明，只要測量出周圍環境溫度，物體初始溫度，以及物體冷卻過程中任意時刻的物體溫度，就可以利用模型（1.3.3）求出將物體冷卻到某一溫度所用的時間或者可以求出者將物體冷卻某一時間物體的溫度.

2.常微分方程數學模型在物體冷卻問題中的應用

在物體冷卻的問題中，存在著因變量對自變量一階導數的關系方程，因此，在物體冷卻問題中，我們常常利用常微分方程數學模型來解決相應的問題.

建立數學模型的思想，可以把復雜的問題簡單化，利用常微分方程的數學模型，可以更便捷的解決物體冷卻中的一些問題，例如法醫在推斷尸體死亡時間時，可以通過尸體的溫度和周圍環境的溫度，大致推斷出死亡時間.再例如，可以通過數學模型計算出物體冷卻過程中物體溫度的變化隨時間的變化之間的規律.

例題 把100℃的一杯水放在室溫25℃的環境中進行冷卻，經過15分鐘水溫為40℃，求水溫達到30℃需要多長時間.

分析 此題利用數學模型（1.3.2），先有初始溫度條件求出K的值，然后由經過15分鐘水溫為40℃的條件求出λ值，最后就可以求出30℃所用的時間了.

解題：開始（t=0）水溫為100℃，由模型T=Q+Ke-^λt可得到：

100=25+KK=75，T=Q+75e-λt

①

把已知條件t=0.25小時 時候T=40℃帶入①中得到：40=25+75e-λ0.25.

315=e-0.25λln315=-0.25λ

λ=-14ln315≈0.40235.

把λ值帶入①中得到：

T=Q+75e-0.40235t.

②

把T=30，Q=25帶入②中得到：

30=25+75e-0.40235t115=e-0.40235tln115=-0.40235tt≈1.09.

則，需要經過約1.09小時后水才能達到30℃.

3.結 語

常微分方程的數學模型不僅在物體冷卻問題中有著重要的作用，而且在其他類似的問題中也具有重要的作用，例如在物體自由下落，汽車剎車，物質衰變，等問題中，同樣可以利用常微分方程來更便捷的解決相應的問題.而對我們來說，關鍵的是要學會建立模型的思想，學會靈活的運用數學模型，在生活中數學無處不在，數學是其他自然科學的工具，我們要在相應的問題中，讓建立數學模型思想也無處不在！