N元環三角形拼接圖三色定理的證明

廖榮寶 朱云 柴蘭蘭

【摘要】為了給四色定理問題的研究提供啟示，本文對N元環經過三角形劃分后所得平面三角形拼接圖的著色問題進行了研究，本文結論可歸納如下.（1）任意N元環劃分所得三角形拼接圖均含有N-2個三角形和N-3條非環上邊.（2）任意N元環劃分所得三角形拼接圖中，至少存在兩個三角形由連續三個環上點構成.（3）任意N元環劃分所得三角形拼接圖都符合三色定理.

【關鍵詞】四色定理;圖論;平面圖;數學歸納法

【中圖分類號】O157 AMS（2000）主題分類：05C15

【基金項目】阜陽師范學院自然科學項目（2013FSKJ05ZD， 2014FSKJ01ZD）

一、引 言

四色定理是圖論中未經證明的一個問題，這一看似簡單的問題被認為是近代三大數學難題之一.這一定理指出，對于任何地圖，采用四種顏色對各個國家進行著色即可保證任何兩個相鄰國家具有不同的顏色，這一問題于1852年由英國制圖員Guthrie提出，距今已有160余年時間.1879年Kempe最早提出被稱作Kempe鏈的“換色法”對于這一假設進行了證明.但1890年，Heawood發現Kempe的證明過程中存在錯誤，指出Kempe實際證明了任何地圖均可實現五著色的命題.1976年，美國數學家Appel、Haken和Kock曾采用計算機經過一百多億次邏輯判斷方法證明了四色定理;但直到21世紀，純粹的數學證明方法依然沒能獲得.

為了給四著色問題的研究提供啟示，本文將進行一類由N個頂點形成的多邊形劃分為三角形拼接圖后所得圖形著色問題的研究.本文將按如下順序進行論述.首先介紹地圖著色問題的簡化處理以及文獻中五色定理的染色方法，然后討論N元環三角形拼接圖的性質，最后證明N元環三角形拼接圖符合三色定理.

二、五色定理簡介

文獻中五色定理的介紹很多，但由于多數文獻采用圖論專業術語進行描述，所以無法達到淺顯易懂的效果.為此，本文作者打算用通俗語言對五色定理進行重新描述，以盡可能地達到無論專業數學工作者或業余數學愛好者均能看懂的效果.

1.地圖著色問題的簡化處理

一般在研究地圖著色問題中可先對地圖進行“點面翻轉”操作，這一操作可具體描述如下.考慮一類簡單地圖，地圖中只存在三個國家交界點的情況且每個國家周圍至少有三個鄰國.此時，每個國家都可看作多邊形“面”，每個三國交界點即為一個“點”;整個地圖有數個多邊形“面”和數個三國交界“點”構成.現把原地圖中每個多邊形“面”變成一個“點”同時把每個三國交界“點”看成一個“面”.如果兩國交界，則用一條線把代表兩個國家的點連接起來.此時原地圖中所有三國交界點均會變成三角形面，原地圖變成由三角形面拼接而成的多面體圖形.為了簡便起見，本文把這種經“點面翻轉”后獲得的由三角形拼接而成的多面體叫做“TH體”（其中T取自triangle，H取自hedron）.原地圖的四著色問題變為研究TH體的四著色問題（下文中字母代表國家，面代表多國交界點）.

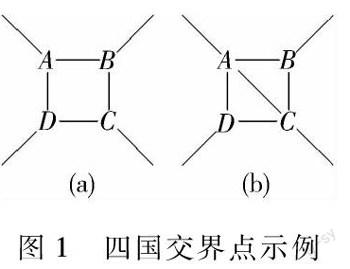
圖1 四國交界點示例 以上TH體中只有三個國家交界的情形，如果實際地圖中存在四個或四個以上國家共享一個交界點的非TH體情形（如美國地圖有四州共用交界點情形）或其他如國中之國以及一個國家只和兩個國家交界的非TH體情形等，均可轉變為TH體.例如一個國家若只與兩個國家交界，則可以先去除這個國家，待完成著色問題后，再將這個國家增添到原來的位置，染上與周邊兩個國家不同的顏色即可.再如，存在四國交界點的情形也可轉變為TH體.如圖1所示（圖1中非四國交界區未畫出），圖1（a）中A，B，C，D四點代表四個國家，四邊形面ABCD代表四國交界點.此時圖1（a）不屬于TH體.但若連接圖1（a）中AC兩點，即可將圖1（a）變為如圖1（b）所示的TH體.若圖1（b）符合四色定理，則斷開AC連線后，所得圖形必然符合四色定理.也就是說，非TH體的著色問題均可通過TH體的著色問題完成.

2.五色定理的相關介紹

五色定理可用數學歸納法證明;即已知四個國家構成的地圖符合五色定理，現假設N個國家構成的地圖符合五色定理，那么若能在此基礎上證明N+1個國家構成的地圖符合五色定理，則命題成立.現以TH體為地圖基本模型描述五色定理的證明過程.

我們先來考察TH體的相關性質.TH體是一種多面體，依據多面體歐拉公式，頂點數（N）、面數（F）、邊數（E）符合式（1）.TH體中每條邊被兩個面共享，每個面均由三條邊構成，所以有式（2）成立，且由式（1）和式（2）可得式（3）.假設TH體中每個點均與其他6個或6個以上點相連，考慮到每條邊被兩個頂點共用，可知TH體的邊數E與頂點數N關系符合式（4）.由于式（4）與式（3）矛盾，可知以上假設不成立.即任意TH體中至少有一個頂點只與5個或5個以下其他頂點相連.

N+F=E+2.

（1）

2E=3F.

（2）

E=3N-6.

（3）

E≥3N.

（4）

因此，對于一個N+1頂點的TH體，必有一個頂點只與5個或5個以下其他頂點連線.若此點與其他3個頂點相連，則可去除此點以及由此點引出的三條連線，獲得一個N頂點的TH體.依據假設，此N頂點TH體可進行五著色.待著色完成后，再把剛去除的這個頂點添加到N頂點TH體原位置上并染上與周圍三點不同的顏色，即可完成N+1頂點TH體的五著色過程.若N+1頂點TH體中有一點與其他四點相連，則去除此點后將產生一個四邊形，把此四邊形劃分為兩個三角形后可獲得一個N頂點TH體.依據假設 N頂點TH體可五著色.待著色完成后將去除的點添加到N頂點TH體原位置上并染上與周圍四點不同的顏色，即可完成N+1頂點TH體的五著色過程.若N+1頂點TH體中有一點與其他五點相連，如圖2（a）中A點，則需檢查B點和D點間有無連線，分別考察B和D有無連線兩種情況.

圖2 A點與周圍五點相連情況 若B和D有連線，則存在三角形面ABD（此三角形面不屬于原N+1頂點TH體的外表面），沿著ABD所在的面將TH體切割為左邊和右邊共兩個共享面ABD的TH體;這兩個TH體的頂點數均小于或等于N，所以這兩個TH體均可五著色.假設用Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ五種顏色對左邊TH體著色，并把A，B，D分別染上Ⅰ、Ⅱ、Ⅲ三種顏色.再假設對右邊TH體采用（1）、（2）、（3）、（4）、（5）五種顏色進行著色，把A，B，D分別染上（1）、（2）、（3）三種顏色.然后用一組新的顏色1、2、3、4、5對以上兩個TH體進行換色操作.用1取代兩TH體中的Ⅰ和（1），用2取代兩TH體中的Ⅱ和（2），用3取代兩TH體中的Ⅲ和（3），用4取代以上兩TH體中的Ⅳ和（4），用5取代兩TH體中的Ⅴ和（5）.則換色后兩個TH體中A，B，D三點對應顏色均為1，2，3.再沿著原切割面ABD把兩個TH體對接起來即得一個符合五色定理的N+1頂點TH體.

若B和D無連線，則去除A點，并把B和D融為一點，如圖2（b）所示.此時N+1頂點TH體變為N頂點TH體，依據假設，任何N頂點TH體均可五著色.待圖2（b）對應的N頂點TH體完成五著色后，將去除的A點恢復并染上與周圍四點不同的顏色即可完成 N+1頂點TH體的五著色過程.至此，我們完成了任意N頂點TH體的五著色證明.

三、N元平面TP圖的著色問題

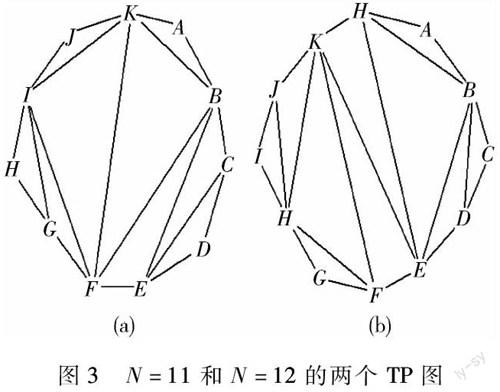
設有N個點兩兩相連構成一個平面N元環.現對平面N元環中的任意兩點進行兩兩相連（要求連線過程中保持任意兩條連線不相交）對N元環進行切割劃分，直至原N元環內沒有四邊形或四條邊以上的多邊形為止，此時稱獲得的平面圖叫“N元平面TP圖”（其中T取自triangle，P取自polygon）.例如，圖3即為N=11和N=12兩個N元平面TP圖的結構示例.接下來我們來研究N元平面TP圖的性質.

圖3 N=11和N=12的兩個TP圖 1.N元平面TP圖的結構

定理1：N元平面TP圖中有N-2個三角形和N-3條環內邊.

證明：N元平面TP圖有N條環上邊;設圖中有K條環內邊和F個三角形.因為每條環內邊被用來構建兩個三角形而每條環上邊只被用來構建一個三角形，所以可得邊數與三角形數的關系式（5）.

2K+N3=F.

（5）

對于一個N元環，在劃分為TP圖過程中內角和不變.所以F個三角形的內角和等于原N元環的內角和，由此得出式（6）.顯然F=N-2，進而可得K=N-3.即N元平面TP圖中有N-2個三角形和N-3條環內邊，證畢.

180F=180（N-2）.

（6）

定理2：N（N>3）元平面TP圖中，至少有兩個三角形為原N（N>3）元環上緊鄰三點構成的三角形.

證明：N元平面TP圖可視為由N-2個三角形拼接而成，且此時圖中有N-3條環內邊和N條環上邊.顯然，當N大于3時N元環上任何連續三條邊不能形成三角形.所以N元平面TP圖中的任何三角形，不可能擁有三條環上邊，即N元TP圖中任意三角形最多擁有兩條環上邊.另外，在N元TP圖中，任意一條環上邊不可能參與構建兩個或兩個以上的三角形.現N頂點TP圖中有N-2個三角形，有N條環上邊.為了盡量少地出現一個三角形擁有兩條環上邊的情況，可讓每個三角形均擁有一條環上邊;此時N-2個三角形共用去N-2條環上邊，但還剩下兩條環上邊.由于任何三角形不能擁有三條環上邊，所以這兩條環上邊只能分別分配到兩個三角形中去.這就造成N（N>3）元TP圖中至少有兩個三角形擁有兩條環上邊.只有環上緊鄰三點才可構成屬于同一個三角形的兩條環上邊，所以至少有兩個三角形為N（N>3）元環上緊鄰三點構成，證畢.

若把某個擁有兩條環上邊的三角形從N頂點TP圖中切除，則可得一個N-1元TP圖，即為這個被切除的擁有兩個環上邊的三角形可看作外接在N-1元TP圖上;我們把這種擁有兩個環上邊的三角形稱為“外接三角形”.

2.N元平面TP圖的三著色證明

圖4 當N=3，4，5時TP圖的三色方案 當N=3，4，5時，若不考慮TP圖中各個點的差別以及各條邊長的差別，則所得TP圖均只有如圖4所示的一種結構花樣（其他結構花樣可由圖4經旋轉獲得，不能獨立存在）.如圖4所示（圖中1，2，3表示三種顏色），N=3，4，5時對應TP圖均可三著色.

定理3：任何N元平面TP圖都可三著色.

證明：現采用數學歸納法證明定理3，假設N元TP圖可以實現三著色，再證明N+1元TP圖也可三著色.定理2指出，N+1（N>3）元平面TP圖中至少有兩個外接三角形，現把其中的一個外接三角形標記為ABC;其中AB和BC均為環上邊，AC為非環上邊.則沿著AC邊切去外接三角形ABC，可獲得一個N元平面TP圖.即此N+1元平面TP圖可以看作由一個N元平面TP圖和一個三角形拼接而成.顯然，切去的三角形是可三著色的，設其三種顏色為Ⅰ、Ⅱ、Ⅲ.依據數學歸納法假設，N元平面TP圖可三著色.現對切割后產生的N元TP圖進行三著色，設對應三種顏色為x、y、z.假設對切割后產生的N元TP圖和三角形ABC分別進行三著色.設N元TP圖中點A和點C分別著色為x和y（其他點著色暫不考慮）;三角形中A，B，C三點分別著色為Ⅰ、Ⅱ、Ⅲ.現用另外三種顏色1，2，3取代N元TP圖和三角形ABC的顏色.取代操作規定為：用1取代x和Ⅰ;用2取代y和Ⅲ;用3取代z和Ⅱ.經過顏色取代后，N元TP圖和三角形ABC中點A均為顏色1，點C均為顏色2;現把兩圖沿切割邊AC拼接起來，則所得N+1元TP圖只具有三種顏色1，2，3，即為N+1元TP圖可三著色.結合圖4中N=3，4，5時可三著色的事實，可知任意N元TP圖均可三著色，證畢.

四、結 論

本文研究了由N元環經連線劃分所得N元平面TP圖的性質.得出N元平面TP圖中有N-2個三角形和N-3條環內邊;且所得三角形中至少有兩個三角形為N元環上緊鄰三點構成.并在此基礎上證明了N元平面TP圖是可三著色的.本文結論對四色定理的證明有一定的啟示意義.在接下來的工作中，我們將在此基礎上逐步展開關于四色定理的后續研究工作.

【參考文獻】

[1]王利民，張利明，呂國：使用四色定理求解圖形著色的數學模型[J].河北建筑工程學院學報，2006（24）：102～103.

[2]王禮萍，王慧蓉：平面圖四色問題的一個必要定理[J].哈爾濱師范大學自然科學學報 2003（19）：29～30.

[3]Kempe，A.B.：On the geographical problem of the four colours[J].American journal of mathematics 1879（2）：193～200.

[4]Kempe，A.：How to color a map with four colours without coloring adjacent districts the same color[J].Nature 1879（20）：275.

[5]Heawood，J.：On the fourcolor map problem[J].Quart.J.Pure Math 1898（29）：270～285.

[6]陳明，李剛：四色定理證明的探討[J].山東理工大學學報：自然科學版 2013（27）：10～12.

[7]Appel，K.，Haken，W.，Koch，J.：Every planar map is four colorable.Part II：Reducibility[J].Illinois Journal of Mathematics 1977（21）：491～567.

[8]謝力同，劉桂真.與四色定理等價的幾個命題[J].應用數學 2000（13）：59～62.