出奇制勝 百戰百勝

張煥萍

【摘要】平面向量是高考中的熱點也是難點，但其解題策略主要包含幾個意識，主要有基底意識，坐標意識，幾何意識，投影意識，內積意識，這對解決向量問題有很大的幫助.

【關鍵詞】 平面向量;基底意識;坐標意識;幾何意識;投影意識;內積意識

綜觀對近幾年高考題中平面向量的思考，發現平面向量的考題中常會涉及向量的長度、夾角、和、差、數量積、投影等概念和知識點，向量試題有越來越綜合、越來越靈活的趨勢，因而在解題方法和解題工具的選擇上尤為顯得重要，選擇不恰當的方法，會比較費時、費力，且不得要領;選擇恰當時，題目甚至可以被“秒殺”，所以在具體的平面向量解題中，對向量解題意識的培養極其重要.

1.基底意識

由平面向量基本定理可知，平面內任意一向量都可用同一組基底進行唯一表示，選取恰當的基底，數形結合，用已知的基底來表示所涉及處理的向量，讓問題轉化成已知基底的運算.這種未知向已知的轉化，充分展示基底方法的優越性.

例1 如圖1在△ABC中，AB=3，AC=4，∠BAC=60°，AB=3AD，AE=EC，求BE·CD的值.

圖 1分析 直接求BE·CD的值需知道BE與CD的模及夾角，顯然無法得到，因已知條件可知線段AB，AC的長與夾角.故選擇適當的兩不共線向量來表示所求的BE與CD，記AB=a，AC=b，

則a=3，b=4，a·b=6，BE=12b-a，CD=13a-b，

∴BE·CD=（12b-a）·（13a-b）=76a·b-12b2-13a2=-4.

2.坐標意識

將平面向量數量化，向量的坐標表示就是一種具體表現，它簡化了向量的分析、繁雜的運算，只要結合向量的坐標運算就能達到目的，這需要我們在審題時發現能否建立直角坐標系來確定一些點的坐標，從而得到所需向量的坐標，再對向量進行運算.

例2 如圖2，在矩形ABCD中，AB=2，BC=2，點E為BC的中點，點F為邊CD上， 若AB·AF=2，則AE·BF=

圖 2 分析 由于AB，BC的長度已知，夾角確定，因此選擇AB，AD為基底，可用基底意識解之，但對特殊圖形容易建系的情況，我們可以將向量用坐標表示加以計算，如圖以A為原點，AB為x軸，垂直于AD為y軸建系，設F（x，2），A（0，0），E（2，1），B（2，0）顯然AF=（x，2），AB=（2，0），得AB·AF=2x=2，

確定得F（1，2），故AE=（2，1），BF=（1-2，2），AE·BF=2（1-2）+1×2=2.

3.幾何意識

向量有著數與形的完美結合，向量的線性運算與數量積都有獨特的幾何意義，數形結合的思想方法的靈活運用，省時省力，可以提高解題的效率.

例3 已知a，b是平面內的兩個單位向量，a·b=12，若向量c滿足=120°，求c的最大值.

分析 本題若采用基底或坐標意識去解決都比較困難，但是用幾何法就相對比較簡單.

∵a·b=12，a=b=1，∴a，b的夾角為60°，又=120°，記 AB=a，AC=b，AD=c，則|AB|=1，|AC|=1，∠BAC=60°，∠BDC=120°，所以可以畫出圖像（圖3）且A，B，C，D四點共圓，△ABC為等邊三角形，則O是△ABC的外心，AD過圓心O時c的模最長，故易得cmax=233.

4.投影意識

向量的數量積的運算包括幾何法和坐標法，幾何法需確定兩向量的模與夾角等基本量，當模與夾角不確定或不易得到的情況下，很難用公式解決，而向量數量積a·b的幾何意義為a的模與b在a上的投影|b|cos的乘積，正因有了“向量的投影”的概念若將其作為一種“整體意識”加以運用，則可事半功倍.

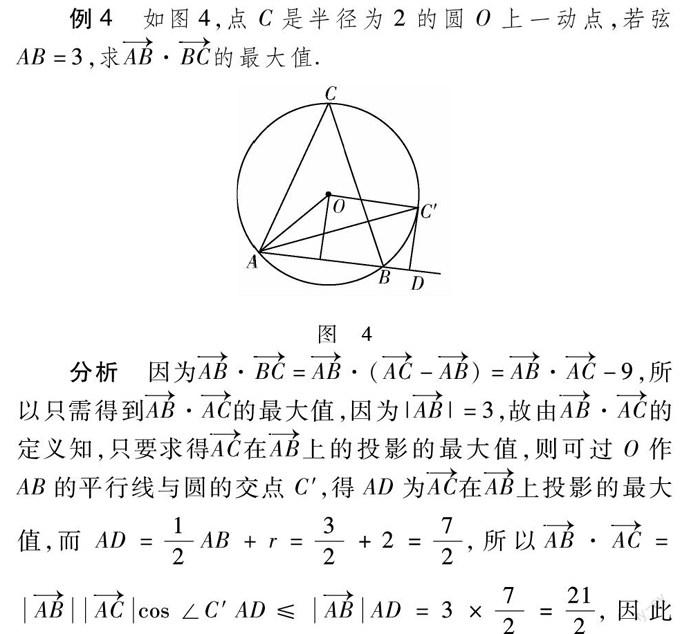
例4 如圖4，點C是半徑為2的圓O上一動點，若弦AB=3，求AB·BC的最大值.

圖 4分析 因為AB·BC=AB·（AC-AB）=AB·AC-9，所以只需得到AB·AC的最大值，因為|AB|=3，故由AB·AC的定義知，只要求得AC在AB上的投影的最大值，則可過O作AB的平行線與圓的交點C′，得AD為AC在AB上投影的最大值，而AD=12AB+r=32+2=72，所以AB·AC=ABACcos∠C′AD≤ABAD=3×72=212，因此（AB·AC）max=212×9=32.

5.內積意識

兩向量的數量積即內積，向量的內積是平面向量的重點，事實上，平面向量的內積對長度、角度等方面有著非常廣泛的應用空間，在求解一些代數問題時，若有目的、有意識在一向量恒等式的兩邊，對同一向量進行數量積，則同樣能收到較滿意的解題效果.即當a=b，則a·c=b·c成立.

例5 已知△ABC所在平面上點P滿足OP=OA+λ（ABABcosB+ACACcosC），λ∈R，則動點P的軌跡一定過△ABC的

心.（填：重心，垂心，外心，內心）

分析 觀察分析條件中出現cosB，cosC，而AB，AC與BC進行內積可與cosB，cosC有密切聯系，因為OP-OA=AP，所以向量恒等式OP=OA+λ（ABABcosB+ACACcosC），λ∈R兩邊可同時對BC進行內積，所以條件可以變為AP·BC=λ（AB·BCABcosB+AC·BCACcosC）=λ（-BC+BC）=0，可得AP⊥BC，則P的軌跡一定過△ABC的垂心.

正如陳武生老師說的，過分強調任何一種方法都不恰當，我們應分清各種方法的作用與功能，理清楚題目向量的條件，這樣才能做到出奇制勝，百戰百勝.