平面幾何最值問題解法探析

趙庭標

【摘要】平面幾何中最值問題綜合性強、能力要求高.解題時要善于運用特殊與一般、轉化、建模等數學思想，靈活運用特殊位置法、軸對稱法、平移法、旋轉法、構造三角形法、判別式法、配方法等各種數學方法，找到幾何最值取得時的位置;或將問題轉化成基本最短路徑模型;或建立方程、函數模型，再求解.

【關鍵詞】平幾最值;解題策略;思想方法

近年來，中考對平面幾何最值問題的考查呈現出最值模式的多樣化和綜合化，題型也由選擇、填空題向解答題變化.本文結合近幾年中考試題，將蘊涵在其中的各種最值問題顯現出來，并探析一些常見最值問題的解題方法.

一、運用特殊與一般的思想—找到幾何最值取得時的位置

1. 特殊位置法

特殊位置法就是利用幾何特征找到幾何最值取得時的位置，然后再求.

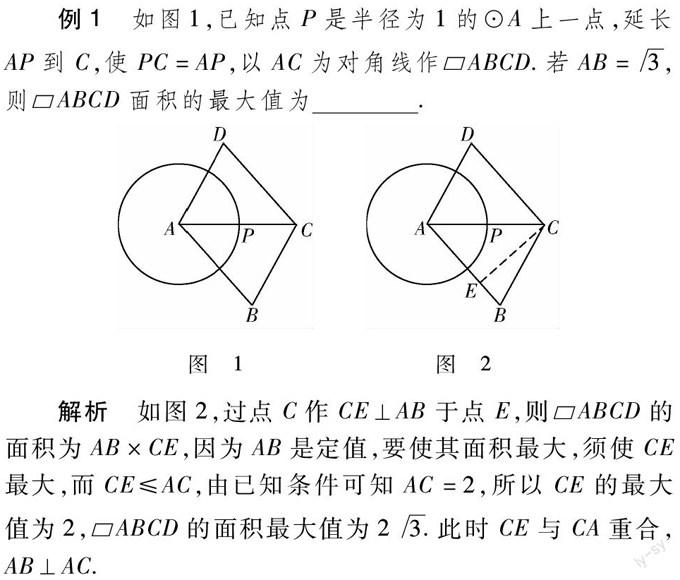
例1 如圖1，已知點P是半徑為1的⊙A上一點，延長AP到C，使PC=AP，以AC為對角線作ABCD.若AB=3，則ABCD面積的最大值為

解析 如圖2，過點C作CE⊥AB于點E，則ABCD的面積為AB×CE，因為AB是定值，要使其面積最大，須使CE最大，而CE≤AC，由已知條件可知AC=2，所以CE的最大值為2，ABCD的面積最大值為23.此時CE與CA重合，AB⊥AC.

本題是運用以退求進的辦法，找到最值取得時的特殊位置.有時要找特殊點、特殊圖形等尋找突破口.

二、運用轉化思想—將問題轉化成基本的最短路徑模型

1. 軸對稱法

當動點在定直線上運動時，可通過作出定點關于定直線的對稱點來剖析動點的位置，稱這種方法叫軸對稱法.

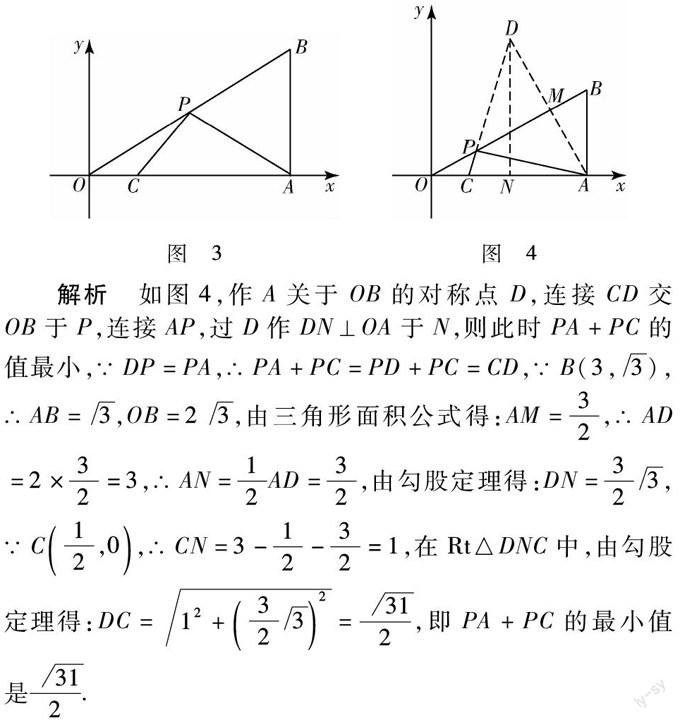
例2 如圖3，在平面直角坐標系中，Rt△OAB的頂點A在x軸的正半軸上.頂點B 的坐標為（3，3），點C的坐標為12，0，點P為斜邊OB上的一個動點，則PA+PC的最小值為（ ）.

A.132 B.312 C.3+192 D.27

解析 如圖4，作A關于OB的對稱點D，連接CD交OB于P，連接AP，過D作DN⊥OA于N，則此時PA+PC的值最小，∵DP=PA，∴PA+PC=PD+PC=CD，∵B（3，3），∴AB=3，OB=23，由三角形面積公式得：AM=32，∴AD=2×32=3，∴AN=12AD=32，由勾股定理得：DN=323，∵C12，0，∴CN=3-12-32=1，在Rt△DNC中，由勾股定理得：DC= 12+3232=312，即PA+PC的最小值是312.

本題是過定點作一條定直線的一次對稱，通過軸對稱將直線“同側”的兩點問題轉化為“異側”的兩點問題，解題關鍵是求出P點的位置，有時要過定點作兩條定直線的兩次對稱

2.平移法

平移法就是根據需要，在平面內把一個圖形沿著一定的方向移動一定的距離.通過平移，將無公共端點的兩條線段轉化為有公共端點.

例3 如圖5，已知直線a//b，且a與b之間的距離為4，點A到直線a的距離為2，點B到直線b的距離為3，AB=230.試在直線a上找一點M，在直線b上找一點N，滿足MN⊥a且AM+MN+NB的長度和最短，則此時AM+NB=（ ）.

A.6B.8C.10D.12

解析 本題是途經一條線段的兩點之間最短路程問題，由于MN表示直線a與直線b之間的距離，是定值，由此只要滿足AM+NB的值最小即可，AM、BN是兩條沒有公共端點的線段，我們可以通過平移把它們接起來，形成“兩點之間線段最短”基本模型.如圖6，把點A沿垂直于直線a的方向向直線b平移4（等于MN的長）到點A′，接下來只要在b上找一點N，使A′N+NB最短即可.因為把點A沿垂直于直線a的方向向直線b平移4（等于MN的長）到點A′，其實就是把AM平移到A′N的位置.因為點A到直線a的距離為2，所以點A平移后的對應點A′也是點A關于直線a的對稱點，所以本題也可以用對稱法解決.

此例通過平移變換，將平行線“外側”的兩點問題轉化為平行線“內側一點”和“外側一點”的問題，進而轉化為“兩點之間，線段最短”基本模型.

3.旋轉法

旋轉法是一種用旋轉變換來解題的方法.此法主要應用在以下兩個方面：一是在題設

條件和結論關系不明顯或條件不易集中利用的情形下，通過旋轉，起到鋪路架橋的作用;二是圖形錯綜復雜，但圖形中的量與量之間的關系多，這時也可以看能否使用旋轉法，移動部分圖形，使題目中隱藏的關系明朗起來，從而找到解題途徑.

例4 在△ABC中，AB=4，BC=6，∠ACB=30°，將△ABC繞點B按逆時針方向旋轉，得到△A1BC1.如圖7，點E為線段AB中點，點P是線段AC上的動點，在△ABC繞點B按順時針方向旋轉的過程中，點P的對應點是點P₁，直接寫出線段EP1長度的最大值與最小值.

解析 如圖7，因為BE是定值，根據“垂線段最短”，所以過點B 作BD⊥AC，D為垂足，當點P在AC上運動至垂足點D時，將△ABC繞點B逆時針旋轉，使點P的對應點P1在線段AB上時，EP1最小（逆時針旋轉到A1C1⊥AB時，此時A1C1與AB的交點P1到點E距離最小）;如圖8，當P在AC上運動至點C時，將△ABC繞點B逆時針旋轉，使點P的對應點P1在線段AB的延長線上時，EP₁最大（逆時針旋轉到BC₁與AB在同一條直線上時，即點A，B，C₁共線時，此時P1到點E距離最大），即可求得線段EP1長度的最大值與最小值，分別為8和 1.

此例用到了“垂線段最短”這個基本模型，這里是通過旋轉變換，找到最值取得時的特殊位置.

三、運用模型思想—建立方程、函數模型

1.判別式法

當一個問題是確定圖形之間的特殊位置關系或者一些特殊的值時，通常利用幾何圖形的性質，建立一元二次方程模型，用根的判別式求解.

例5 如圖9，正方形ABCD邊長為1，當M，N分別在BC，CD上，使得△CMN的周長為2，則△AMN的面積的最小值為

解析 如圖10，延長CB至L，使BL=DN，則Rt△ABL≌Rt△ADN，故AL=AN，又∵CM+CN+MN=2，CN+DN+CM+BM=1+1=2，∴MN=DN+BM=BL+BM=ML，進而求證△AMN≌△AML，即可求得∠MAN=∠MAL=45°設CM=x，CN=y，MN=z，根據x2+y2=z2，和x+y+z=2，得（2-y-z）2+y2=z2，整理得 2y2+（2z-4）y+（4-4z）=0.由△=4（z-2）2-32（1-z）≥0，得（z+2-22）（z+2+22）≥0，又因為z>0，所以z≥22-2，此時，s△AMN=S△AML=12ML·AB=12Z，因此，當z=22-2時，s△AMN取得最小值2-1.

2.配方法

當一個問題是確定有關圖形的變量之間的關系時通常建立函數模型通過配方求解.

例6 如圖11，直線l與半徑為4的⊙O相切于點A，P是⊙O上的一個動點（不與點A重合），過點P作PB⊥l，垂足為B，連接PA.設PA=x，PB=y，則（x-y）的最大值是

.

解析：本題若用幾何方法，通過幾何模型，用幾何的手段對動點的位置展開研究很難找到解題突破口，我們不妨考慮用代數的方法，利用函數的有限區間或二次函數性質求最值.如何用函數的手段刻畫“線長”的解析式呢？如圖12，由題意，作直徑AC，連接CP，得出△APC∽△PBA，利用APAC=BPAP得出y=18x2，所以x-y=x-18x2=-18x2+x=-18（x-4）2+2.

當x=4時，x-y有最大值是2.

通過以上各例的剖析我們不難發現平面幾何中最值問題形式較多，但大致可分為求線段的長度、角的度數、圖形的面積這三類，解題方法也比較多，概括起來主要是運用了轉化思想、模型思想、特殊與一般的思想.如“最短距離問題”，我們在研究時常常利用軸對稱、平移等變換，將諸多如“將軍飲馬問題”、“造橋選址問題”、三角形周長最小、四邊形周長最小等問題轉化成基本最短路徑模型（點與點的距離或點與線的距離），還有一些幾何最值問題可轉化為代數問題去解決，其關鍵是根據幾何性質建立關系式，利用完全平方公式、一元二次方程根的判別式、二次函數性質從數與形結合的角度求解.有時要注意取值范圍的限制.這也可以說是一種“模型思想”;另一種是根據特殊與一般的思想，利用幾何特征找到幾何最值取得時的位置，然后再求.常見的幾何最值模型有：兩點之間線段最短，垂線段最短、三角形三邊關系、平行線間的距離最短，直徑是圓中最長的弦，弧的中點到弧所對弦的距離最長等.對于個別特殊的幾何最值問題，可根據周長與面積的關系，利用以下兩個重要結論求解：邊數相同周長相等的多邊形中以正多邊形的面積最大.反過來，面積相等的平面圖形中以圓的周長最小.

【參考文獻】

[1]馬小為.中學數學解題思想方法技巧[M].西安：陜西師范大學出版社，2009.

[2]李承勇.例談平面幾何中幾種最值問題[J].中學數學教學參考（中旬），2013（6）：49-51.