高中數(shù)學：習題對比在數(shù)學思維能力訓練中的重要性

胡金利

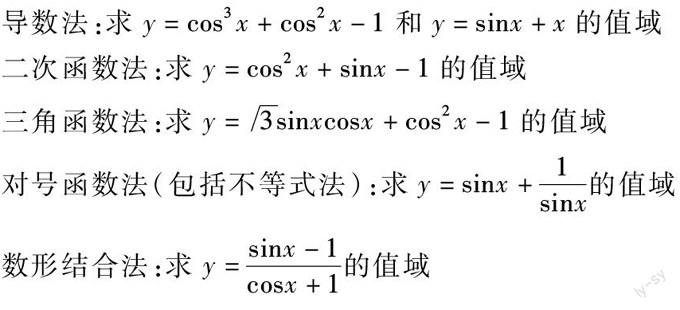
【摘要】在數(shù)學學習中，真正的難點不在于對具體知識的理解，而是知識脈絡的梳理.習題作為思維啟發(fā)和思維傳遞的重要載體，是構建數(shù)學思維的最重要的途徑.本文以習題對比為核心，談一談這一教學方法對于訓練學生數(shù)學思維能力的重要意義.

【關鍵詞】習題對比;數(shù)學思維能力

一直以來，大家都將多做題作為收獲成績的重要途徑，太過于關注做題的“量”，而忽略了題目的“質”及其暗含的數(shù)學思想.學生們越來越多的關注題目的答案是什么，而不是“如何對題目進行分析”，大家開始通過記憶的方式“積攢”做題的思路和方法，而不是尋找思路的本源從而將方法進行整合.很多學生在做題時，大多依靠“回憶”所帶來的“直覺”，一旦無法搜尋到類似的記憶或出現(xiàn)了記憶缺失，考試成績就會發(fā)生較大的波動.因此，筆者非常反對學生考試前幾天學生熬夜看書、通宵復習，因為對數(shù)學考試的目的不是對記憶的考驗，而是學生掌握數(shù)學思想和方法的程度的體現(xiàn).

在提高學生做題“質量”的實踐中，筆者特別強調“習題對比”的重要性.習題對比與習題練習不同，它將習題以某些共性為篩選依據(jù)，通過“習題系”的方式進行呈現(xiàn)，強調學生對于習題間聯(lián)系和區(qū)別的對比和分析，并從中有所領悟，對抽象的知識有更加具體、全面、深入的了解.因此，本文中，筆者將通過對“習題對比”方法和實例的闡述，具體介紹“習題對比”在加深學生對新知的認知、進行知識整合、掌握數(shù)學解題技巧中的作用，從而展示這一方法對于促進學生數(shù)學思維能力提升的重要意義.

一、習題對比對加深新知認知的作用

在新知講解的過程中，習題對比就是通過“習題系”呈現(xiàn)新知與舊知的對比，進而達到對新知更加深入、全面、系統(tǒng)的認知的目的.在具體操作時，筆者通常在“邏輯指導”和“經(jīng)驗指導”兩種思維方式的共同作用下，進行習題系的確定.所謂“邏輯指導”，是指將知識進行拆分，確定可能造成學生思維難度的觀察角度，并與可用的知識進行對比出題;所謂“經(jīng)驗指導”，是指根據(jù)以往的經(jīng)驗，及學生學習的反饋，對“邏輯指導”下產生的方案進行重要程度的排列及進一步的修正和優(yōu)化.接下來，筆者將通過實例來進行闡述.

案例1：集合表示方法——描述法的習題選取 這一部分的“習題選取”是針對高一數(shù)學教學而言，不涉及高三數(shù)學復習過程中關于這一知識的習題選取.

在邏輯指導和經(jīng)驗指導的共同作用下，發(fā)現(xiàn)學生對于集合描述法的易錯點在于對下屬兩個要素的理解：①要觀察的元素;②所觀察元素的共同特征.于是，采取對比的方式，將這一知識點和初中、高中已經(jīng)學過的知識進行對比理解.經(jīng)過這一過程后，筆者形成了這樣的習題對比方案：通過對比{1，2，3，4}和{x|1≤x≤4，x∈Z}，讓學生體會描述法和列舉法的優(yōu)缺點;通過{x|1≤x≤4，x∈Z}和{x∈Z|1≤x≤4}、{x|1≤x≤4，x∈Z}和{k|1≤k≤4，k∈Z}、{x|1≤x≤4，x∈Z}和1x|1≤x≤4，x∈Z、A=x∈N61+x∈Z和B=61+x∈Z | x∈N的四組對比，讓學生明白觀察元素有很多種展現(xiàn)方法，不必拘泥;通過對比{x|1≤x≤4，x∈Z}和{（x，y）|x+y=1}讓學生進一步體會元素特征中數(shù)集和點集的區(qū)別.

由此可見，筆者所謂的“習題對比”，其實就是針對每一個訓練目標而列舉出“習題系”，通過對習題系內題目的對比、分析，讓學生能夠對所學知識有更加靈活、全面的掌握.在具體的應用中，還會根據(jù)學生的反饋、新提出的問題等，對這些習題系進行不斷的修正和豐滿.

二、習題對比對知識整合的作用

高考與平時的模塊考試最大的不同，就在于所包含的知識的廣度.在模塊考試中，學生已經(jīng)對可能用到的知識有了預期，在對題目的思考上，已經(jīng)有了一個基本的方向.但是在高考中，所考核的知識已經(jīng)不再局限于某一模塊的范圍，因此，學生的一個很大的困惑，就是他們不知道對于面對的問題，到底有哪些知識可以用.于是，當他們遇到思維的障礙，他們無法判斷到底是自己沒有將已有的知識運用好，還是有一個自己沒想到、可能也想不到的新解法，從而只能選擇放棄.針對于這一問題的解決，習題對比彰顯了無窮的魅力.在以知識整合為目的的習題對比中，筆者通常使用“同一問題篩選法”來進行“習題系”的確定.所謂“同一問題篩選法”，就是將同樣的問題放在高中所有的知識領域里，看是否能夠進行結合，從而篩選出對于同一問題有用的知識點，進而再根據(jù)已篩選的知識進行題目的選取和對比.接下來，筆者將以“和三角函數(shù)有關的求值域”為例，具體闡述如何通過習題對比促進學生的知識整合和思維構建.

案例2：和三角函數(shù)有關的求值域 在這一部分的闡述中，筆者假定，學生已經(jīng)掌握了跟三角函數(shù)有關的公式、定義、圖像等相關知識，已經(jīng)掌握了函數(shù)y=Asin（ωx+φ）的值域的求法（高三總復習用）

這一問題，主要是在講述函數(shù)y=Asin（ωx+φ）的值域的過程中出現(xiàn)的.考慮到在高中數(shù)學階段，講述了非常多的和求值域有關的知識，因此，筆者在講述函數(shù)y=Asin（ωx+φ）的值域時，通過習題對比，加深學生對于和值域有關的知識的理解.根據(jù)“同一問題篩選法”，筆者形成了一下的習題對比思路：

導數(shù)法：求y=cos3x+cos2x-1和y=sinx+x的值域

二次函數(shù)法：求y=cos2x+sinx-1的值域

三角函數(shù)法：求y=3sinxcosx+cos2x-1的值域

對號函數(shù)法（包括不等式法）：求y=sinx+1sinx的值域

數(shù)形結合法：求y=sinx-1cosx+1的值域

通過上述對比學生會發(fā)現(xiàn)，雖然都有三角函數(shù)的元素，但是我們要透過題目的現(xiàn)象看透本質，在深入理解各類知識點的聯(lián)系和區(qū)別的基礎之上，切中題目要害，從而循序找出正確的思路.

三、習題對比對數(shù)學解題技巧的作用

之所以提出“數(shù)學解題技巧”這一概念，是由于數(shù)學學習過程中，總有一些題目的答案是“非常規(guī)”的.學生對于這一類“非常規(guī)”的做法非常的看重，認為這是取得關鍵分數(shù)的法寶，從而將這些做法“記錄”下來.其實，這些“非常規(guī)”的做法都是基于一些數(shù)學思想自然而然的想到的，只要學生掌握了一些數(shù)學思想和處理技巧，在對題目進行簡單的分析之后，這些方法就會呼之欲出.

因此，在對“非常規(guī)”解題方法進行講解時，筆者更加看重習題的對比，希望通過常規(guī)解法和非常規(guī)解法的比較，讓學生領會一些數(shù)學技巧和方法，從而學會技巧性解題.

下面，筆者將從幾個案例入手，通過習題對比談一談“留誰”這一話題進背后的“先易后難”這一解題技巧.

案例3：解析幾何——留“x”還是“y”

先來看兩道習題：

習題1：設F1，F(xiàn)2分別為橢圓C：x2a2+y2b2=1（a>b>0）的左右焦點，過F2（2，0）的直線l與橢圓C相交于A，B兩點，直線l的傾斜角為60°，若|AB|=154，求橢圓C的方程

習題2：設F1，F(xiàn)2分別為橢圓C：x2a2+y2b2=1（a>b>0）的左右焦點，過F2（2，0）的直線l與橢圓C相交于A，B兩點，直線l的傾斜角為60°，如果AF2=2F2B，求橢圓C的方程.

習題1是我們最常見的類型題，其處理方式是將直線方程和橢圓方程連立，通過消去y，得到一個關于x的一元二次方程.而習題二，我們通過得到AF2=2F2Bx1+2x2=4和-y1=2y2，考慮到計算的便捷性，最終采取的是橢圓方程和直線連立，消去x，得到一個關于y的一元二次方程，然后繼續(xù)求解.大多數(shù)有關解析幾何的習題，都是保留x作為運算的主體，而習題2卻選擇保留y作為運算的主體，學生理解的薄弱環(huán)節(jié)恰恰就在于為何進行運算主體的“轉換”.

筆者在講解時，通常會引入一個解題技巧：“先易后難”，即“誰簡單，就先對誰進行運算”.以“習題系”為例，在習題1中，我們在發(fā)現(xiàn)，如果保留y作為運算主體，并沒有降低運算難度，所以按照習慣，我們保留x作為運算主體.在習題2中，我們發(fā)現(xiàn)，式子-y1=2y2較為簡單（只有比例關系），出于“先易后難”的思想，我們從簡單的元素開始嘗試，如果嘗試失敗，再重新將思路回歸到常規(guī)的方法中.

由此可見，“先易后難”這種處理技巧其實是給了學生一個思維邏輯，基于這一邏輯，學生可以很自然的完成思路的選擇，由此，很多新解法也就從解法的“創(chuàng)新”轉變成了一種思維的靈活運用，達到了促進學生數(shù)學思維構建和數(shù)學思維訓練的目的.在高中數(shù)學階段，這一思想在解決其他有關“留誰”的問題上，同樣適用.

案例4：數(shù)列——留“an”還是“Sn”

同樣的，先來看習題3和習題4：

習題3：已知Sn為數(shù)列an的前n項和，且Sn=nan（n>1），a1=1，求an的通項公式.

習題4：已知Sn為數(shù)列an的前n項和，a1=1，且n>1時，2S2n=2anSn-an，求an的通項公式.

這兩道題看似基本相同，但是在式子的處理上卻完全到不同，前者應用Sn-Sn-1=an保留an，用著應用an=Sn-Sn-1保留Sn.對于這一差異的解釋，同樣可以運用“先易后難”的思想.對于Sn=nan來說，Sn是單獨存在的，并沒有涉及其他運算，因此我們采取保留an的方案，先對Sn進行運算.而對于2S2n=2anSn-an來說，雖然兩者都涉及了一些運算，但是比較來看，Sn涉及了平方、乘積多種運算，相對復雜，因此我們采取保留Sn的方案，先對an進行運算.

案例5：微積分——“∫A dx”還是“∫A dy”

闡述之初，我們先來通過對比的方式看看習題5、習題6：求曲線xy=1及直線y=x，y=2圍成的封閉圖形的面積（習題5）;求曲線y=2x-x2和y=2x2-4x圍成的封閉圖形的面積（習題6）.在解答時，很多輔導資料給出的答案為：習題5以y為積分變量，S=∫21（y-1y）dy=32-ln2;習題6以x為積分變量，S=∫20[（2x-x2）-（2x2-4x）] dx=4.疑問顯而易見，同樣是用微積分求面積，為什么有的是以x為積分變量，有的是以y為積分變量呢？為了解決這一疑惑，筆者在教學過程中首先會用“以x為積分變量”的方法來探索解決所有的題目，并告訴學生：

1.“以x為積分變量”可作為思考此類問題的常用思路.

2.對于習題5來說，如果用“以x為積分變量”的方法來解，需要將x的范圍進行分段，將整體圖形分成兩個部分，即：S=∫112（2-1x）dx-∫21（2-x）dx.如果嘗試以y為積分變量，就可以不用將圖形進行拆分.比較來看，“以y為積分變量”在某種意義上更為簡單，選用這種方法正是“先易后難”的思想的體現(xiàn).

3.在高中階段，由于我們接觸到的微積分難度有限，并沒有真正體會到不同積分變量的選取所帶來的便捷性，但同學們要理解這兩種思維的含義，在大學階段的學習過程中，進行進一步的加深理解.

通過以上闡述不難發(fā)現(xiàn)，習題對比在教學中有著非常重要的作用，是對學生數(shù)學思維能力進行訓練的一個非常重要的手段.因此，筆者提倡，在習題練習的過程中，教師一定要充分發(fā)揮習題對比的重要性作用，以加深學生對于知識的認知，進而促進學生數(shù)學思維的整合和構建，達到對學生進行思維能力訓練的目的.