參數(shù)假設(shè)檢驗(yàn)中的兩類錯(cuò)誤
沈榮瀘

【摘要】本文在正態(tài)總體的總體均值右側(cè)假設(shè)檢驗(yàn)前提下,對(duì)假設(shè)檢驗(yàn)的兩類錯(cuò)誤進(jìn)行探討,進(jìn)而得出犯兩種錯(cuò)誤的概率α和β的關(guān)系式,最后在得到的關(guān)系式下形成三點(diǎn)結(jié)論.
【關(guān)鍵詞】假設(shè)檢驗(yàn);小概率原理;抽樣分布;棄真錯(cuò)誤;納偽錯(cuò)誤
參數(shù)假設(shè)檢驗(yàn)是根據(jù)總體的理論分布和小概率原理,對(duì)未知或不完全知道的總體提出兩種彼此對(duì)立的假設(shè),然后由樣本的實(shí)際結(jié)果,借助相應(yīng)的抽樣分布,經(jīng)過(guò)一定的計(jì)算,對(duì)兩種彼此對(duì)立的假設(shè)在一定概率前提下作出推斷.下面針對(duì)總體未知參數(shù)均值μ進(jìn)行展開.
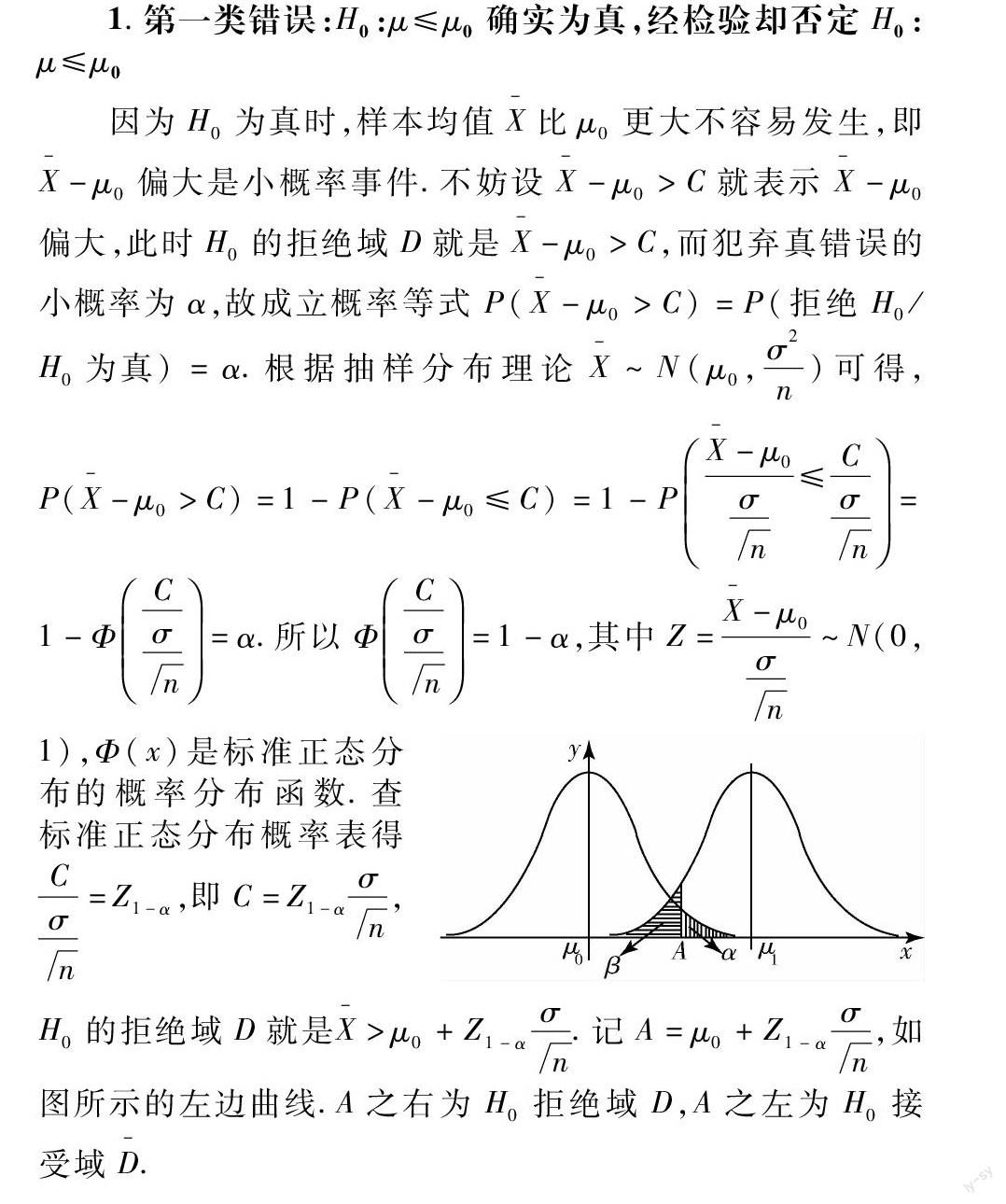
參數(shù)假設(shè)檢驗(yàn)中相互對(duì)立的兩種假設(shè)通常稱為原假設(shè)H0和備擇假設(shè)H1,由于是利用樣本信息對(duì)總體參數(shù)進(jìn)行推斷,所以有可能犯以下兩類錯(cuò)誤:第一類錯(cuò)誤,也叫棄真錯(cuò)誤,當(dāng)原假設(shè)H0確實(shí)為真時(shí),而樣本統(tǒng)計(jì)量的值卻落入拒絕域D內(nèi),從而作出否定H0的推斷,若將犯第一類錯(cuò)誤的概率記為α(通常稱為顯著性水平或檢驗(yàn)水平),則滿足概率等式P(拒絕H0/H0為真)=α;第二類錯(cuò)誤,也叫納偽錯(cuò)誤,當(dāng)原假設(shè)H0確實(shí)為假,即H1為真時(shí),而樣本統(tǒng)計(jì)量的值卻落入接受域D-內(nèi),從而接受H0,若將犯第二類錯(cuò)誤的概率記為β,此時(shí)滿足概率等式P(接受H0/H0為假)=β或P(接受H0/H1為真)=β;為了便于說(shuō)明,我們用正態(tài)總體X~N(μ,σ2)下,方差σ2已知,對(duì)總體均值μ的右側(cè)檢驗(yàn)來(lái)進(jìn)行說(shuō)明.此時(shí)原假設(shè)為H0:μ≤μ0;備擇假設(shè)為H1:μ=μ1>μ0.從總體X中抽取樣本容量為n的簡(jiǎn)單隨機(jī)樣本,其樣本均值為X-.

