“知識發明”教學法示例：歐拉角教學設計

穆華　吳美平　潘獻飛

[摘 要]大學課堂教學的一種成功方式是引導學生自己將所要講授的知識重新“發明”出來。大學老師提出一個或多個問題作為引子，然后引導學生利用已有知識解決所提出的引子問題，并在解決問題的過程中推導出新知識。這種“知識發明”的教學方式有利于調動學生的主觀能動性，營造良好的課堂氛圍，提高學生解決問題的能力，幫助學生構建系統的知識結構。

[關鍵詞]歐拉角 教學設計 知識發明

[中圖分類號] G642 [文獻標識碼] A [文章編號] 2095-3437（2015）03-0163-03

所謂“知識發明”教學法，是指老師在課堂教學中設計合理的問題，引導學生利用已有的知識解決問題，并在解決問題的過程中“發明”出新知識的一種教學方式。全國數學名師李尚志在教學中推行這種教學方式，他在自己編著的教材《線性代數》[1]中寫到：“不從定義出發而從問題出發引入概念，引導學生在嘗試解決這些問題的過程中將所要講授的知識重新‘發明出來”。我們在教學實踐中積極采用“知識發明”教學法，嘗試通過引導學生解決問題來組織課堂教學，收到了良好的教學效果。本文以本科導航類專業課程中歐拉角的教學設計為例，來說明這種教學方式。描述空間直角坐標系（下文簡稱“坐標系”）空間關系的歐拉角在理論力學[2]、飛行力學[3] [4]和導航專業課程[5] [6]中都有所涉及。學生在不同課程中多次學習相關內容后，往往還存在以下問題：不能快速找出兩個坐標系之間的歐拉角，對12種歐拉角的存在性心存疑惑等等。究其原因，從教材編寫到老師授課，往往把重點放在結論上，直接把結論灌輸給學生。如果按照教材編寫授課，歐拉角的引入通常是一句話“歐拉首先提出可以用三個角度來描述剛體的轉動”。接下來就是“拿來主義”，將歐拉提出的歐拉角拿來用。但是學生對于這種拿來的東西往往只知其一、不知其二，很難真正擁為己有。我們在教學實踐中嘗試引導學生自己把歐拉角“發明”出來，這種課堂教學有助于調動學生的學習興趣，使學生自主更新知識體系，從而優化教學效果。

一、歐拉角的引入

兩個平面直角坐標系的空間關系用一個轉角就可以刻畫，這是學生所熟悉的，由此引申到空間直角坐標系，請學生思考：能否用轉角來刻畫兩個空間直角坐標系的空間關系？

（一）引子問題

設O-xpypzp和O-xqyqzq是兩個原點重合、坐標軸方向不重合的空間直角坐標系，分別以P和Q表示。確定兩個坐標系的空間關系可以通過確定坐標系Q在坐標系P中的位置來實現，這相當于取坐標系P為參考坐標系。那么如何確定坐標系Q在坐標系P中的位置呢？

（二）解答

兩個平面直角坐標系的空間關系用一個轉角就可以刻畫。能否用轉角來刻畫兩個空間直角坐標系的空間關系呢？

確定坐標系Q在坐標系P中的位置，只需依次確定坐標系Q的兩個坐標軸的位置，以依次確定Oxq軸和Oyq軸的位置為例。

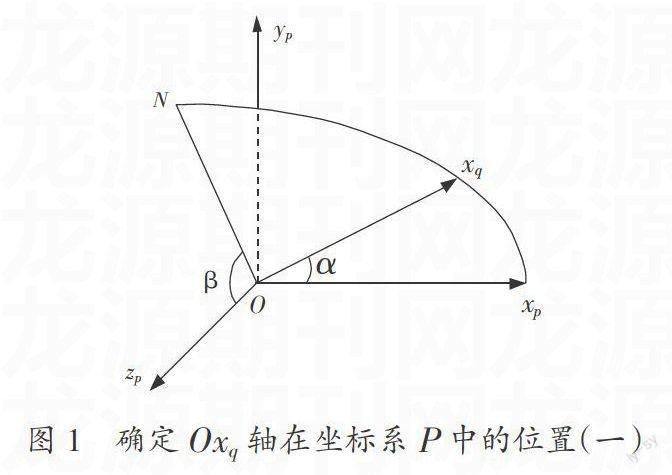
首先確定Oxq軸。在圖1中，ON是Oxq軸與OxP軸所在平面OxqxP與平面OypzP的交線，同時是Oxq軸在平面OypzP內的投影。ON到OzP軸的轉角記為β，OxP軸到Oxq軸的轉角記為α。兩個轉角可以唯一確定Oxq軸在坐標系P中的位置。對于轉角，規定逆時針轉動為正，轉角取值范圍限制為（-180°，180°）。

Oxq軸的位置確定后，由于Oyq軸被限定在Oxq軸的垂面內，所以只需要一個角度來確定Oyq軸在垂面內的位置便可以確定Oyq的空間位置。Oxq軸和Oyq軸的位置確定后，Ozq軸的位置由右手法則確定。可見，可以利用三個轉角確定一個坐標系相對于另外一個坐標系的空間關系。

（三）點評

利用兩個轉角刻畫Oxq軸在坐標系P中的位置，這種方式也提供了通過兩次轉動使得OxP軸與Oxq軸重合的方案。

（1）首先，坐標系P繞OxP軸轉動角度90°-β，使得OyP軸與ON重合，得到的中間坐標系記作Ox′P y′P z′P；

（2）接下來，中間坐標系Ox′P y′P z′P 繞OzP 軸轉動角度α，便可以使得Ox′P 軸與Oxq軸重合，得到的中間坐標系記作Ox″P y″P z″P。

當坐標系P經過兩次轉動使得OxP軸與Oxq軸重合后，中間坐標系Ox″P y″P z″P的Oy″P軸與Oyq軸同位于Oxq軸的垂面內，Oyq的空間位置可以用Oy″P軸到Oyq軸的轉角γ來刻畫。同時，只需將中間坐標系Ox″P y″P z″P再繞重合的坐標軸Oxq軸轉動角度γ，便可以使得坐標系P與坐標系Q重合。可見，三個轉角<90°-β，α，γ>及轉動順序（1、3、1）（這里1、2、3分別表示坐標系的x軸、y軸、z軸）可以完整刻畫兩個坐標系的空間關系。這里的轉角就稱作歐拉角。至此，我們順理成章的引入了歐拉角的概念。

二、歐拉角的分析

（一）歐拉角的組數

顯然，用歐拉角確定兩個原點重合坐標系的空間關系有多種選擇。一方面，通過兩次轉動重合的坐標軸可以在第一軸、第二軸和第三軸之間任意選擇；另一方面，通過兩次轉動使一組坐標軸重合也有多種實現方式。下面以Oxq軸與Oxp軸重合為例，分析所有實現方式。

（1）利用Oxq軸與Oxp軸所在平面Oxqxp（見圖1）。在對引子問題解答的點評中，給出了按照1、3順序轉動的方案<90°-β，α>。也可以采用另一種方案使得Oxp軸與Oxq軸重合。首先坐標系P繞Oxp軸轉動，使得Ozp軸與ON重合，然后繞中間坐標系的Oy′P 轉動使Ox′P 軸與Oxq軸重合。兩次轉動的角度分別為-β和-α，轉動順序為1、2。

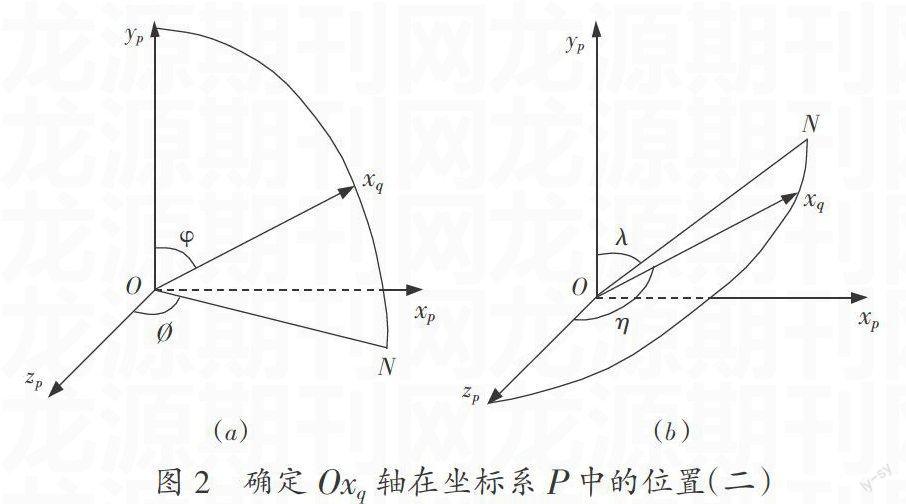
（2）利用Oxq軸與Oyp軸所在平面Oxqxp（見圖2a）。只有一種方案：先繞2軸轉動使得Oxp軸與ON（Oxq軸在平面Oxpzp的投影）重合，然后繞3軸轉動到達Oxq軸的位置。兩次轉動的角度分別為？覫-90°和90°-φ，轉動順序為2、3。

（3）利用Oxq軸與Ozp軸所在平面Oxqzp（見圖2b）。只有一種方案：先繞3軸轉動使得Oxp軸與ON（Oxq軸在平面Oxpyp的投影）重合，然后繞2軸轉動到達Oxq軸的位置。兩次轉動的角度分別為90°-λ和η-90°，轉動順序為3、2。

可見，通過兩次轉動使一組坐標軸重合有四種轉法，相應的首先使該組坐標軸重合，然后再使兩個坐標系重合的轉法也就有四種，對應四組歐拉角。轉動使兩個坐標系重合時首先重合的軸有三種選擇，因此使兩個坐標系重合的轉法有12種，對應12組歐拉角。

（二）特殊情況

本文所考慮的兩個坐標系的坐標軸方向不重合。當兩個坐標系的1軸共坐標系P的坐標平面，即Oxq軸位于平面Oxpyp或者平面Oxpzp內時，上述四種轉動方案退化為兩種。以Oxq軸位于平面Oxpyp內為例，設Oxp軸到Oxq軸的轉角為θ，一種方案為按照1、2順序轉動<-90°，-θ>，另一種方案為繞3軸轉動θ。此時，如果兩個坐標系的2軸和3軸均不共坐標系P的坐標平面，那么使兩個坐標系重合的歐拉角有10組，其中一組僅有兩個歐拉角。如果兩個坐標系的另外一組坐標軸也共坐標平面，例如Oxq軸位于平面Oxpyp內，同時Oyq軸位于平面Oypzp內時，使兩個坐標系重合的歐拉角有8組，其中兩組僅有兩個歐拉角。

（三）確定坐標系轉換的歐拉角

在可以實現兩個坐標系轉換的多組歐拉角中，有些歐拉角可以由已知條件直接獲得。清楚歐拉角的來源，可以幫助學生快速確定合適的歐拉角及轉動順序。考慮下面的例子。

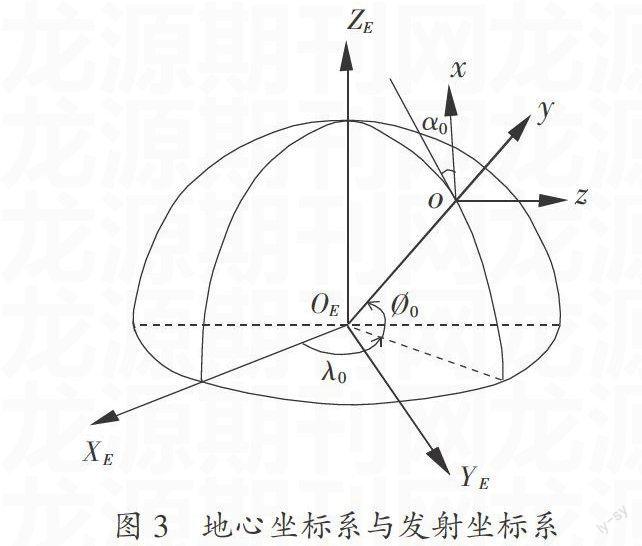
設地球為一圓球，地心坐標系的原點在地心OE，OEXE軸在赤道平面內指向發射時刻的起始子午線并隨地球一起轉動，OEZE軸垂直于赤道平面指向北極。發射坐標系的原點與發射點o固連，發射點的經度為λ0、地心緯度為？覫0；ox軸在發射點水平面內，與o點正北方向的夾角為α0；oy軸垂直于發射點水平面指向上方。如圖3所示。

從歐拉角的引入過程不難體會到，確定歐拉角關鍵是要找到兩個坐標系的某兩個軸所在的平面，并且能夠確定這個平面在參考坐標系中的位置及平面內兩個坐標軸的相對位置。在圖3中，發射點o所在子午面正是這樣一個平面，它是oy軸和OEZE軸所在平面，其位置可以用發射點的經度λ0來刻畫，子午面內oy軸的位置可以用發射點的地心緯度？覫0描述。由此可以確定使地心坐標系與發射坐標系各對應軸平行的三個歐拉角，λ0-90°、？覫0、-（-90°+α0），轉動順序為3、1、2。

說明：這部分屬于后續教學內容，不屬于本次課內容。這里是為了表明學生自己“發明”歐拉角后，在確定坐標系轉換的歐拉角時可以更加得心應手，因此老師在后續課堂教學中可以少用課時。

三、結束語

對于通過解決問題引入新知識的教學方式，我們有以下體會：

1）設計的問題要容易解決，這樣才能調動學生的積極性。在本次教學設計中，引子問題的求解僅用到了中學幾何知識，能夠調動學生的積極性和信心。

2）與傳統教學相比，這種教學方式可能需要多一些教學時間；但是由于學生對新知識的理解更為深刻，所以后續教學往往可以少用課時，總的教學時間是相當的，而教學效果會更好。在本次課中，讓學生自己“發明”歐拉角的方式比“歐拉提出了歐拉角”一句話引入方式用的課時要多一些，但在后續教學“常用坐標系及其相互轉換”中學生可以很快的確定常用坐標系之間的歐拉角，與傳統教學方式相比可以少用課時。

[ 參 考 文 獻 ]

[1] 李尚志.線性代數[M].北京：高等教育出版社，2011.

[2] 孫世賢.理論力學教程[M].長沙：國防科技大學出版社，2009.

[3] 錢杏芳，林瑞雄，趙亞男.導彈飛行力學[M].北京：北京理工大學出版社，2011.

[4] 胡小平，吳美平，王海麗.導彈飛行力學基礎[M].長沙：國防科技大學出版社，2006.

[5] Titterton D.H.and Weston J.L.，Strapdown Inertial Navigation Technology[M]，2nd Ed，The Institution of Electrical Engineers，2004.

[6] Grewal M.S.，Weill L.R. and Andrews A.P.，Global Positioning Systems，Inertial Navigation and Integration [M]，New York：Wiley，2001.

[責任編輯：林志恒]