考慮多故障模式的新型裝備更新保修費用預(yù)測

賈云獻，李欣玥，王 鵬，鄒 效

（1.軍械工程學(xué)院裝備指揮與管理系，河北石家莊050003；2.Pratt ＆Whitney可靠性部門，加利福尼亞圣地亞哥92130）

考慮多故障模式的新型裝備更新保修費用預(yù)測

賈云獻1，李欣玥1，王 鵬2，鄒 效1

（1.軍械工程學(xué)院裝備指揮與管理系，河北石家莊050003；2.Pratt ＆Whitney可靠性部門，加利福尼亞圣地亞哥92130）

立足我軍裝備維修保障實際需求，設(shè)計了保修策略體系。然后，在此基礎(chǔ)上，針對裝備更新保修策略費用難預(yù)測問題，結(jié)合新型裝備多故障模式實際，建立考慮多故障模式的一維更新保修策略費用模型。建立了串聯(lián)系統(tǒng)、并聯(lián)系統(tǒng)、混聯(lián)系統(tǒng)和冷儲備系統(tǒng)的多部件多故障模式費用預(yù)測模型。最后，以冷儲備系統(tǒng)為例進行了案例分析，驗證了模型的有效性和實用性，為我軍開展軍民融合式裝備維修保障建設(shè)提供理論指導(dǎo)和技術(shù)支持。

多故障模式；多部件；更新保修；費用模型

0 引 言

大批新型裝備陸續(xù)列裝部隊，顯著提高了部隊的作戰(zhàn)能力，同時也向部隊裝備維修保障能力提出了更新更高要求。經(jīng)過多年建設(shè)，我軍裝備維修保障能力雖然得到了提升，但要完全依靠建制力量完成新型裝備的深度修理、重大任務(wù)專項保障等工作仍有較大難度。保修作為引入承制方技術(shù)力量的重要途徑，可將承制單位這一地方保障力量最大程度“嵌入”到裝備維修保障系統(tǒng)中，以滿足部隊在平時訓(xùn)練和實際作戰(zhàn)中對裝備戰(zhàn)備完好性的需求。裝備保修服務(wù)一般分為兩類［1］：一類是初始保修服務(wù)，也稱質(zhì)保服務(wù)，初始保修費用一般涵蓋在裝備一次性采購費用中［2］；另一類是延伸保修服務(wù)，屬于裝備技術(shù)服務(wù)范疇，延伸保修費用一般需要軍方額外支付［3］。

目前我軍對保修的管理較為薄弱，實際運作過程中缺乏適合我軍軍情的具體決策技術(shù)支持，致使保修效果不理想、軍地責任劃分不清、雙方利益沖突明顯、軍地力量無法有效融合，嚴重影響了保修服務(wù)在我軍裝備保障中的有效開展。可見，積極開展保修服務(wù)研究有助于深入推進軍民融合式裝備維修保障深度發(fā)展。保修費用預(yù)測是保修服務(wù)研究的重點之一，也是難點之一。合理的保修費用，可使軍方和承制方快速達成價格共識，加快軍民融合速度。由于保修費用受很多因素（裝備可靠性、保修策略等）影響，所以準確預(yù)測保修費用并非易事。鑒于此，本文以系統(tǒng)工程理論為指導(dǎo)，結(jié)合我軍裝備保障實際，著眼于裝備保修服務(wù)內(nèi)在屬性和規(guī)律，系統(tǒng)設(shè)計保修服務(wù)策略體系，并重點研究多故障模式產(chǎn)品更新保修策略費用預(yù)測問題。

1 裝備保修策略體系

保修策略是保修費用重要影響因素，不同的保修策略，費用差異也較大。有多種因素可能影響到保修策略的選擇，如保修對象數(shù)量、保修更新機制、保修維度等。保修服務(wù)在國外受到較多關(guān)注，系統(tǒng)性的研究成果也較多［4－7］，但國內(nèi)對保修策略研究成果較少［8］。本文在文獻［9］對保修分類體系的基礎(chǔ)上，考慮我軍裝備保障的實際需求，設(shè)計裝備保障策略體系如圖1所示。

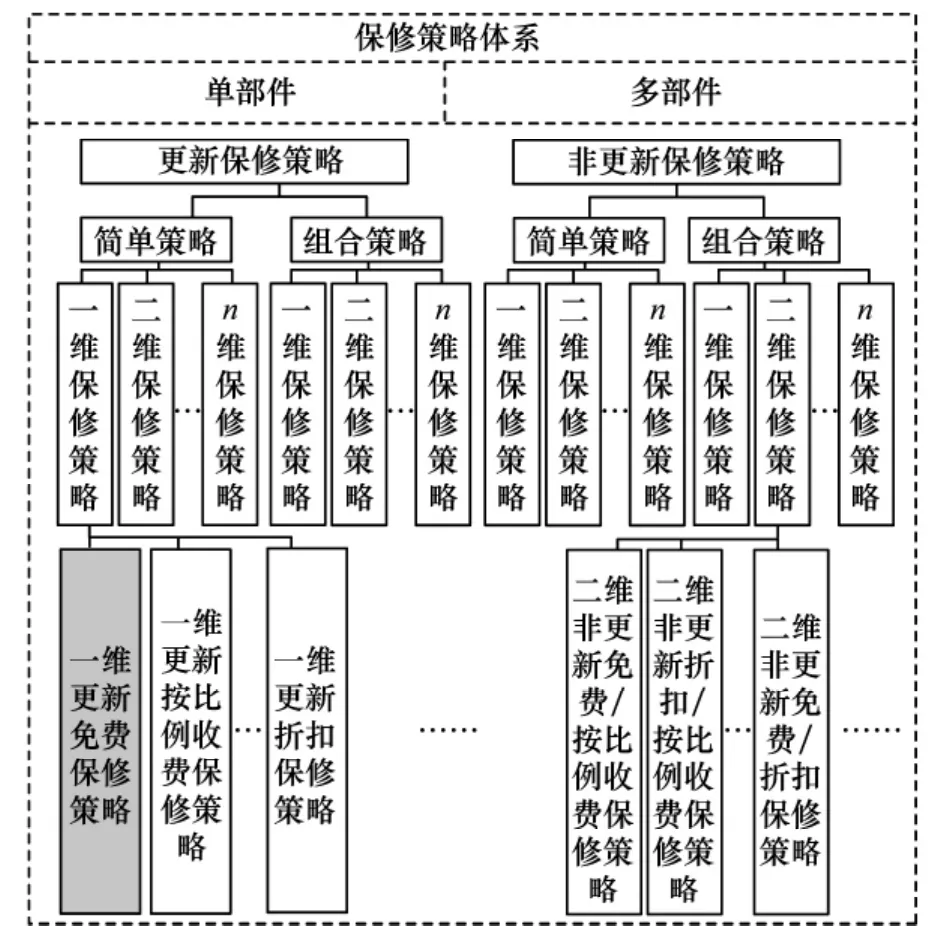
圖1 保修策略體系

首先從保修對象數(shù)量上進行分類，分為單部件保修和多部件保修。單部件保修一般針對一個系統(tǒng)或單元［10－11］，而多部件保修是涉及多個系統(tǒng)或單元之間的聯(lián)合保修［12］。然后保修策略可繼續(xù)分為兩類：更新保修策略和非更新保修策略。更新保修策略是指在保修期w內(nèi)某時刻t進行維修后保修期重新開始直至w＋t［13－14］。更新保修適合于可靠性指標要求較高的單元，例如一些飛機上的輔助動力單元（auxiliary power unit，APU）、發(fā)動機、起落架、導(dǎo)航系統(tǒng)、飛控計算機等子系統(tǒng)。這些子系統(tǒng)能從飛機上拆換，并且拆換時不損傷飛機結(jié)構(gòu)完整性，可以使用更新保修策略。非更新保修策略則是無論保修期W內(nèi)進行多少次維修活動，到w時保修終止［15－16］。簡單策略是指在保修期w內(nèi)僅使用一種保修策略［17］，而組合保修策略是指在保修期w不同階段里采用不同的保修策略［18］。針對不同的保修策略，可以進一步根據(jù)保修期限計量單位數(shù)量分為一維保修、二維保修到n維保修。一維保修期限由日歷時間確定［19］，二維保修期限一般由日歷時間和使用度（如行駛里程，轉(zhuǎn)數(shù)等）共同確定［20－22］。針對一些使用程度要求嚴格的單元，可能需要利用多個使用程度指標約束保修期限，保修策略就可能從一維、二維擴展到n維。保修策略與維修策略的最大區(qū)別在于，保修策略的制定是制造商和使用者雙方博弈的結(jié)果。其費用分攤機制會很大程度上影響到保修決策和保修效果。因此，還需根據(jù)費用分攤方法將不同維的更新或非更新簡單保修策略分為：免費保修、按比例收費保修和折扣保修。其中，免費保修是指保修期內(nèi)活動的所有費用由承制方負責。按比例收費或折扣保修都是將保修期間內(nèi)維修活動產(chǎn)生的費用根據(jù)一定計算方法由軍方和裝備承制單位共同承擔［23］。分攤費用對激勵承制單位在保修期內(nèi)引入預(yù)防性維修具有積極作用［24］。

在裝備保修實踐過程中，對故障單元進行維修時，可能會采取新品更換策略，這就屬于更新保修策略的范疇。更新保修策略所產(chǎn)生的費用較難計算［14，17］，目前，相關(guān)文獻都是針對單一故障模式的費用計算。然而在工程實際中，對復(fù)雜裝備進行更新保修時經(jīng)常會面臨多部件多故障模式的情況［25］，這使得更新保修費用預(yù)測更加困難。因此，本文重點對多故障模式產(chǎn)品更新保修策略費用預(yù)測開展研究。

2 問題描述和模型假設(shè)

下面對考慮多故障模式的一維更新免費保修策略進行建模研究。首先針對單部件的多故障模式保修費用模型進行推導(dǎo)，然后以此為基礎(chǔ)，擴展到多部件的更新保修費用模型。

2.1 單部件系統(tǒng)的更新保修策略費用模型

研究單部件更新保修是研究多部件更新保修的基礎(chǔ)，故先建立單部件多故障模式的更新保修費用模型。假設(shè)對單元進行保修，故障后進行更換，單元修復(fù)如新。更換后保修期重新開始計時，直到保修期內(nèi)不發(fā)生故障為止。設(shè)定的更新保修期長度為w，根據(jù)更新機制，其實際保修期長度T為：T＝t1＋t2＋…＋tNs＋w。

系統(tǒng)的故障次數(shù)為Ns，ti（i＝1，2，…，Ns）為發(fā)生第i次故障的時間間隔。Ns為離散型隨機變量，根據(jù)保修更新機制內(nèi)涵，可得Ns的概率分布列［13］為

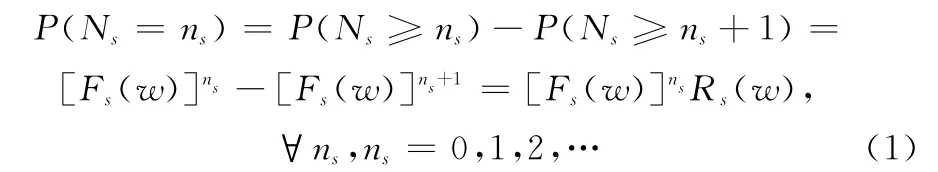
式中，F(xiàn)s（w）和Rs（w）為單元w時刻的累積故障概率和可靠度。假設(shè)單部件有k個故障模式，每個故障模式的修理費用為Ci（i＝1，2，…，k）。則保修費用的期望值和方差值為

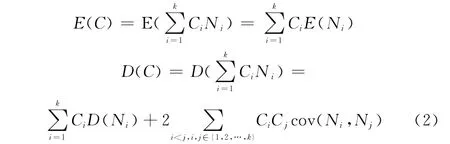
式中，Ni為第i個故障模式在T內(nèi)的故障次數(shù)。第i個故障模式引發(fā)單元故障的概率pi（w）為

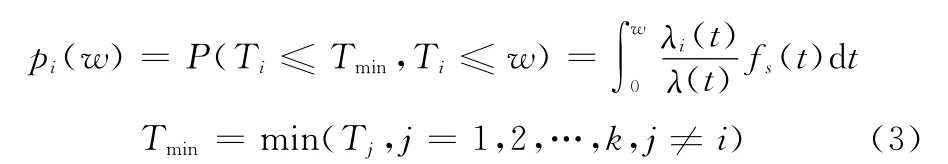
式中，λi（t）為第i個故障模式的故障率函數(shù)；λ（t）為單元的故障率函數(shù)，λ（t）＝；fs（t）為單元故障概率密度函數(shù)。當單元故障次數(shù)為Ns＝ns時，各故障模式的發(fā)生故障次數(shù)的條件聯(lián)合概率函數(shù)符合多項式分布：

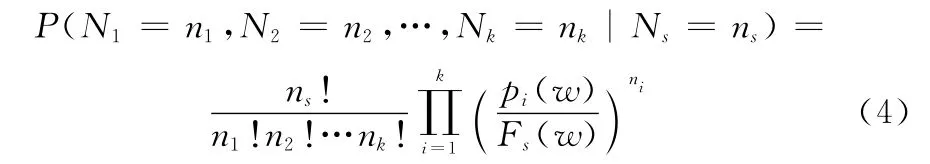
其中，累積故障分布函數(shù)：

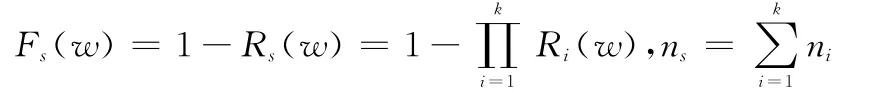
式中，Ri（w）表示第i個故障模式w時刻的可靠度。由多項分布特性可知：

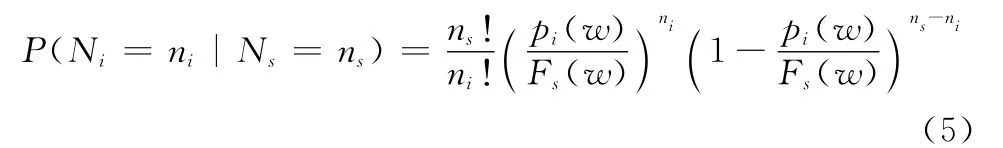
其中，利用矩母函數(shù)和條件期望可得：

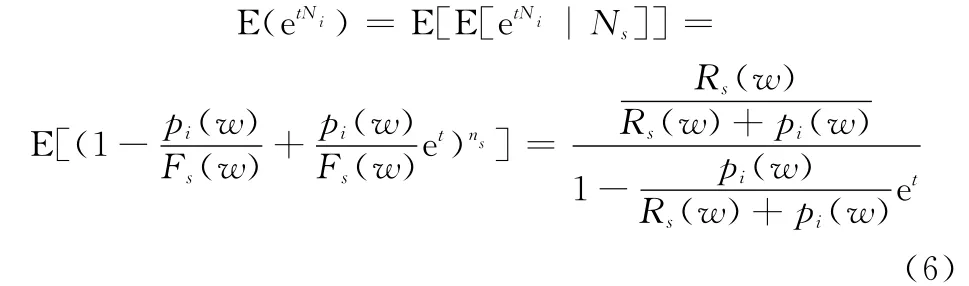
可見，Ni符合幾何分布，表達式為

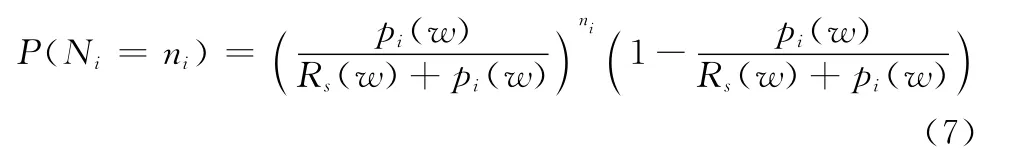
根據(jù)幾何分布特性，Ni的期望和方差為

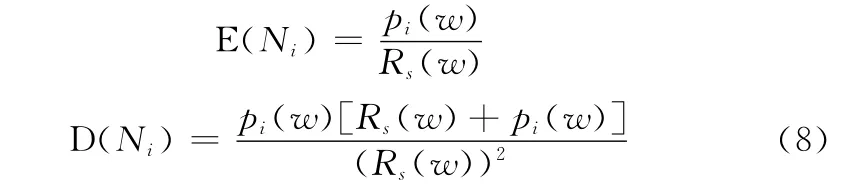
不妨設(shè)ns＝ni＋nj＋nq，根據(jù)式（4）和條件概率函數(shù)性質(zhì)可知：

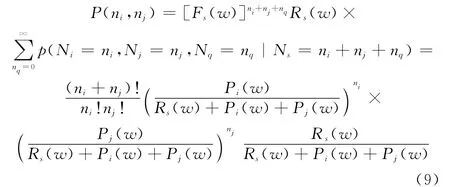
由式（8）和式（9）可知：

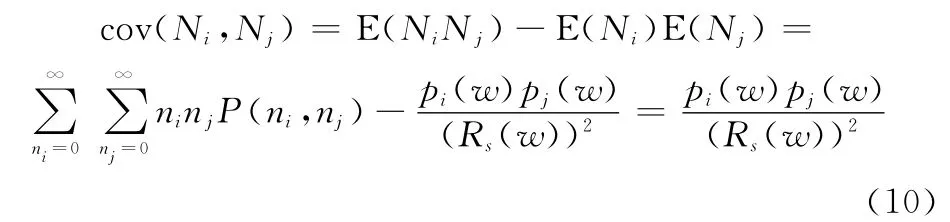
因此，單部件更新保修費用的期望和方差為

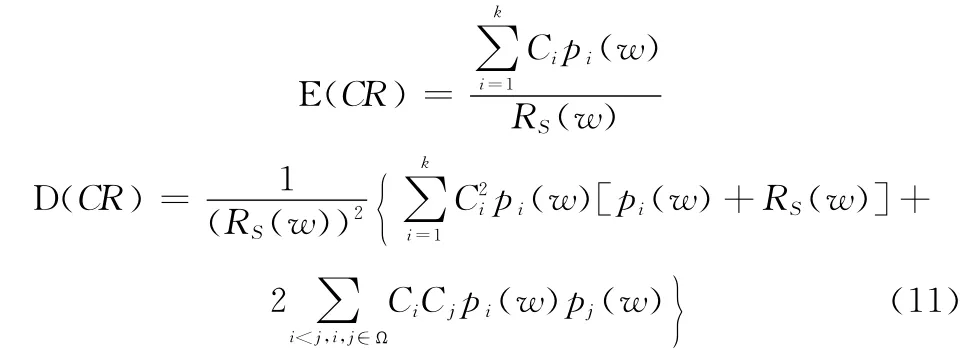
2.2 多部件系統(tǒng)的更新保修策略費用模型

系統(tǒng)一般由多個單元組成，每個單元具有多個故障模式，如圖2所示。下面以第2.1節(jié)為基礎(chǔ)，對幾種常見的系統(tǒng)結(jié)構(gòu)進行更新保修費用建模，建立多部件更新保修策略費用模型。

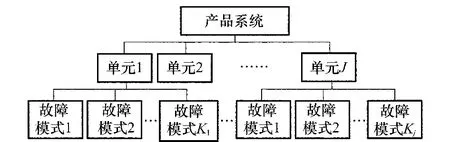
圖2 系統(tǒng)構(gòu)成圖

2.2.1 串聯(lián)系統(tǒng)

假設(shè)多部件系統(tǒng)由J個相互獨立的單元串聯(lián)，每個單元包含ki（i＝1，2，…，J）個相互獨立的故障模式，對不同的單元不同的故障模式，維修費用Cij不同。串聯(lián)系統(tǒng)中任一單元的任一故障模式均會導(dǎo)致整個系統(tǒng)故障。因此，類似單部件的費用模型，串聯(lián)系統(tǒng)的費用模型為

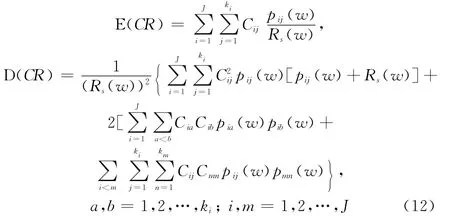
其中

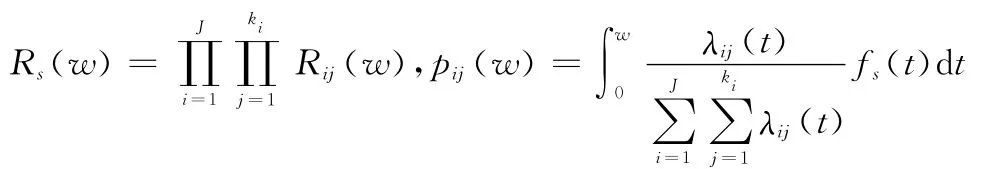
式中，pij（w）為串聯(lián)系統(tǒng)第i個單元的第j個故障模式w時刻引發(fā)單元故障的概率；λij（t）為系統(tǒng)第i個單元的第j個故障模式的故障率函數(shù)；Rij（w）表示串聯(lián)系統(tǒng)第i個單元的第j個故障模式w時刻的可靠度；Rs（w）為單元w時刻的可靠度；fs（t）為單元故障概率密度函數(shù)。

2.2.2 并聯(lián)系統(tǒng)

假設(shè)多部件系統(tǒng)由J個相互獨立的單元并聯(lián)，每個單元包含ki（i＝1，2，…，J）個相互獨立的故障模式，對不同的單元不同的故障模式，維修費用Cij不同。并聯(lián)系統(tǒng)所有單元故障時系統(tǒng)才會發(fā)生故障，由此故障特性可知Ns（i＝1，2，…，J）。并聯(lián)系統(tǒng)的費用模型為

其中

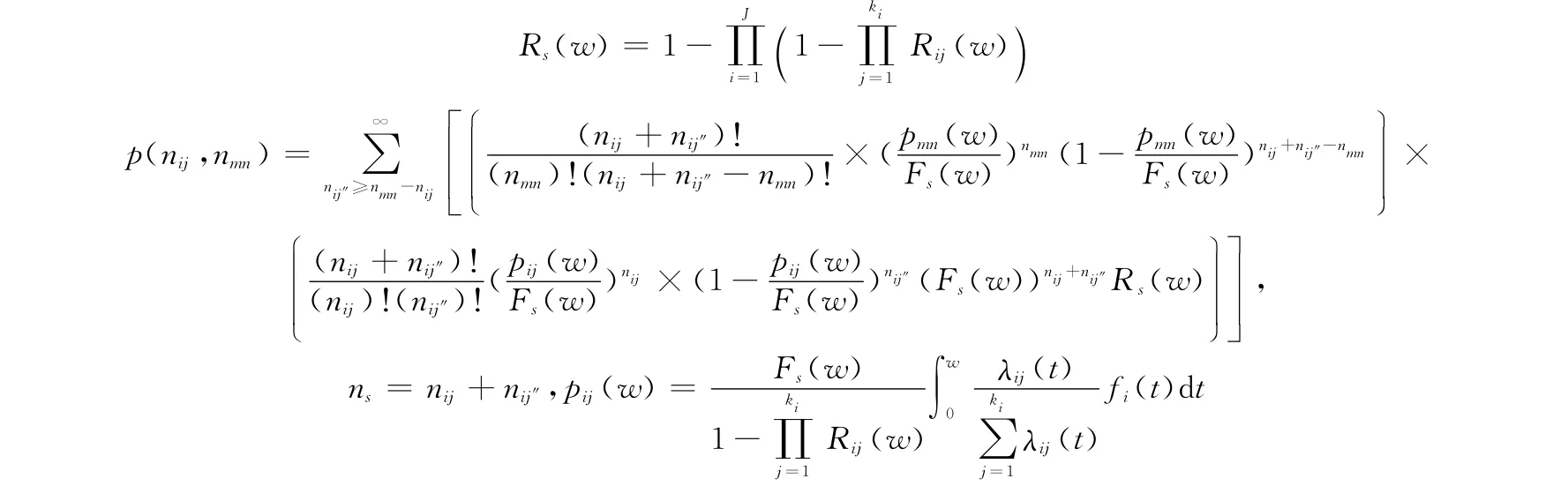
式中，pij（w）為并聯(lián)系統(tǒng)第i個單元的第j個故障模式w時刻引發(fā)單元故障的概率；Rij（w）表示第i個單元的第j個故障模式w時刻的可靠度；Rs（w）和Fs（w）為單元w時刻的可靠度和累積故障概率；fi（t）為并聯(lián)系統(tǒng)第i個單元的故障概率密度函數(shù)；λij（t）為系統(tǒng)第i個單元的第j個故障模式的故障率函數(shù)。

2.2.3 混聯(lián)系統(tǒng)

由串聯(lián)系統(tǒng)和并聯(lián)系統(tǒng)混合而成的系統(tǒng)為混聯(lián)系統(tǒng)，不同的組合模式形成不同的混聯(lián)系統(tǒng)。由于其組成的復(fù)雜性，下面僅以并串聯(lián)系統(tǒng)為例進行費用預(yù)測研究。并串聯(lián)系統(tǒng)是一種特殊的混聯(lián)系統(tǒng)，單元先串聯(lián)后并聯(lián)，可靠性框圖如圖3所示，ri（i＝1，…，q）表示第i行有ri個單元。

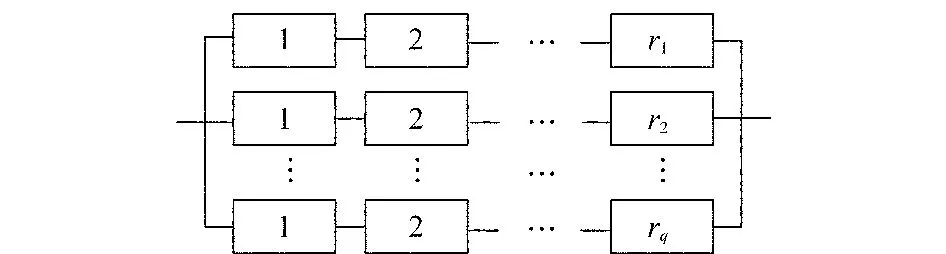
圖3 并串聯(lián)系統(tǒng)可靠性框圖

可見，系統(tǒng)在w時刻的可靠度為

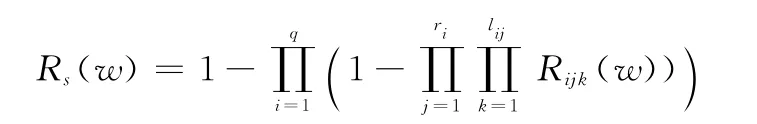
式中，Rijk（w）表示第i行第j個單元的第k個故障模式（一共有l(wèi)ij個故障模式）w時刻的可靠度，該系統(tǒng)費用的期望和方差為

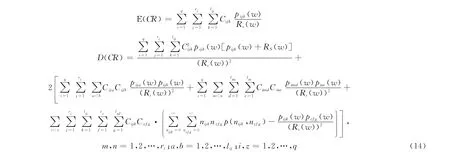
其中

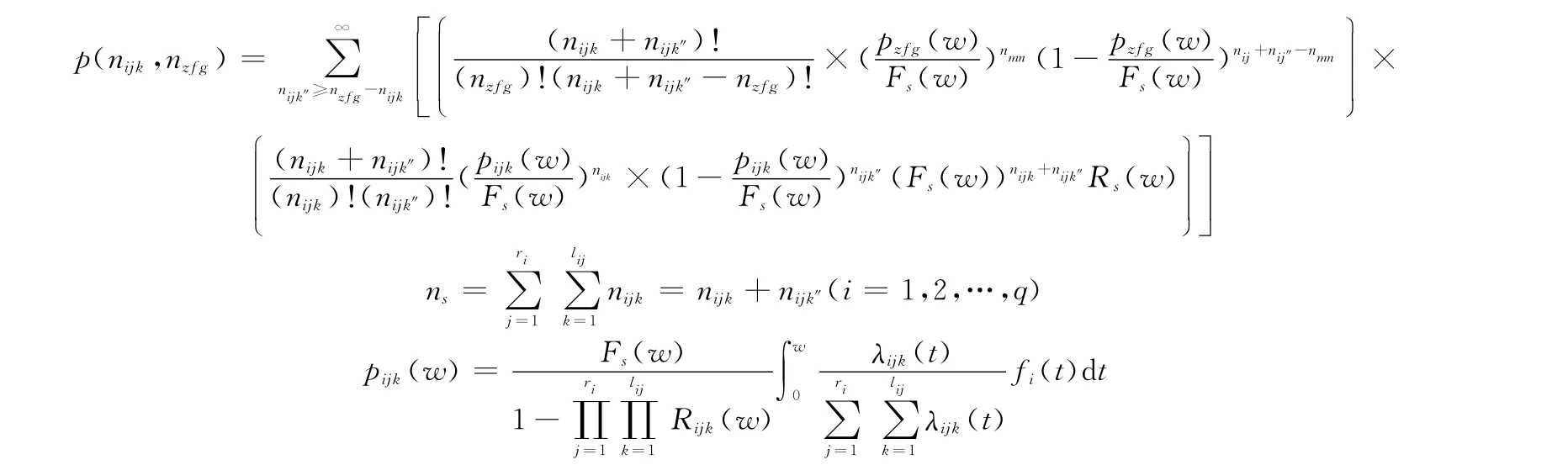
式中，Pijk（w）表示第i行第j個單元的第k個故障模式w時刻引發(fā)單元故障的概率；λijk（t）為第i行第j個單元的第k個故障模式的故障率函數(shù)；fi（t）為串并聯(lián)系統(tǒng)第i行子系統(tǒng)的故障概率密度函數(shù)；Fs（w）為單元w時刻的累積故障概率。

2.2.4 冷儲備系統(tǒng)

對于冷儲備系統(tǒng)，儲備單元可以使用同型同故障模式的單元，也可能是不同型的單元。采用不同型冷儲備系統(tǒng)的原因是避免同一故障原因引發(fā)儲備單元連續(xù)故障，該類系統(tǒng)常見于航天可回收重復(fù)使用系統(tǒng)，例如備用供電系統(tǒng)可能采用柴油發(fā)電機和燃料電池等作為冷儲備系統(tǒng)中單元。有J個單元，每個單元有ki個故障模式所組成的冷儲備系統(tǒng)的可靠性為

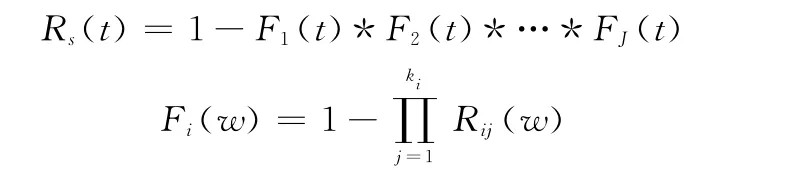
式中，＊為卷積符號。假設(shè)其轉(zhuǎn)換開關(guān)可靠時，費用模型為

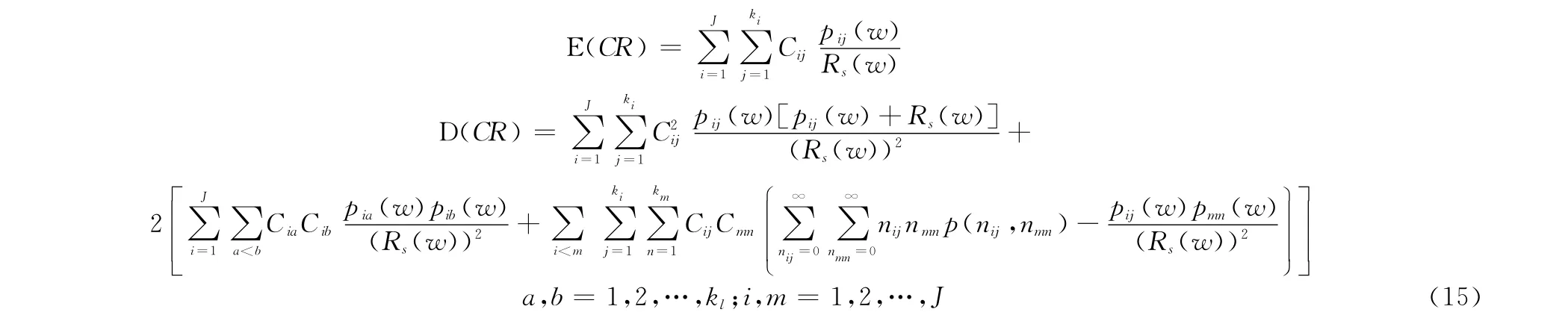
其中

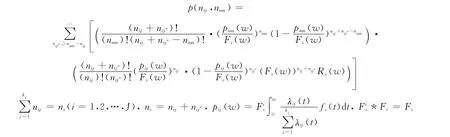
式中，pij（w）為冷儲備系統(tǒng)第i個單元的第j個故障模式w時刻引發(fā)單元故障的概率；Rij（w）表示第i個單元的第j個故障模式w時刻的可靠度；Rs（w）和Fs（w）為單元w時刻的可靠度和累積故障概率；fi（t）為第i個單元的故障概率密度函數(shù)；λij（t）為系統(tǒng)第i個單元的第j個故障模式的故障率函數(shù)。

3 算例分析

以冷儲備系統(tǒng)為例，進行算例分析。假設(shè)系統(tǒng)中包含兩個故障單元，系統(tǒng)可靠性框圖如圖4所示。單元1和單元2各包括兩個故障模式。假設(shè)轉(zhuǎn)換開關(guān)可靠且各故障模式對應(yīng)的概率密度函數(shù)和維修費用如表1所示。

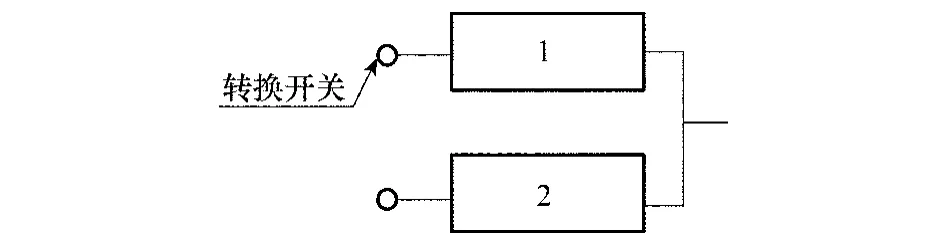
圖4 冷儲備系統(tǒng)可靠性框圖

表1 系統(tǒng)各單元參數(shù)

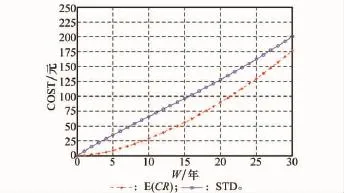
圖5 不同保修期更新保修期望費用和費用標準差

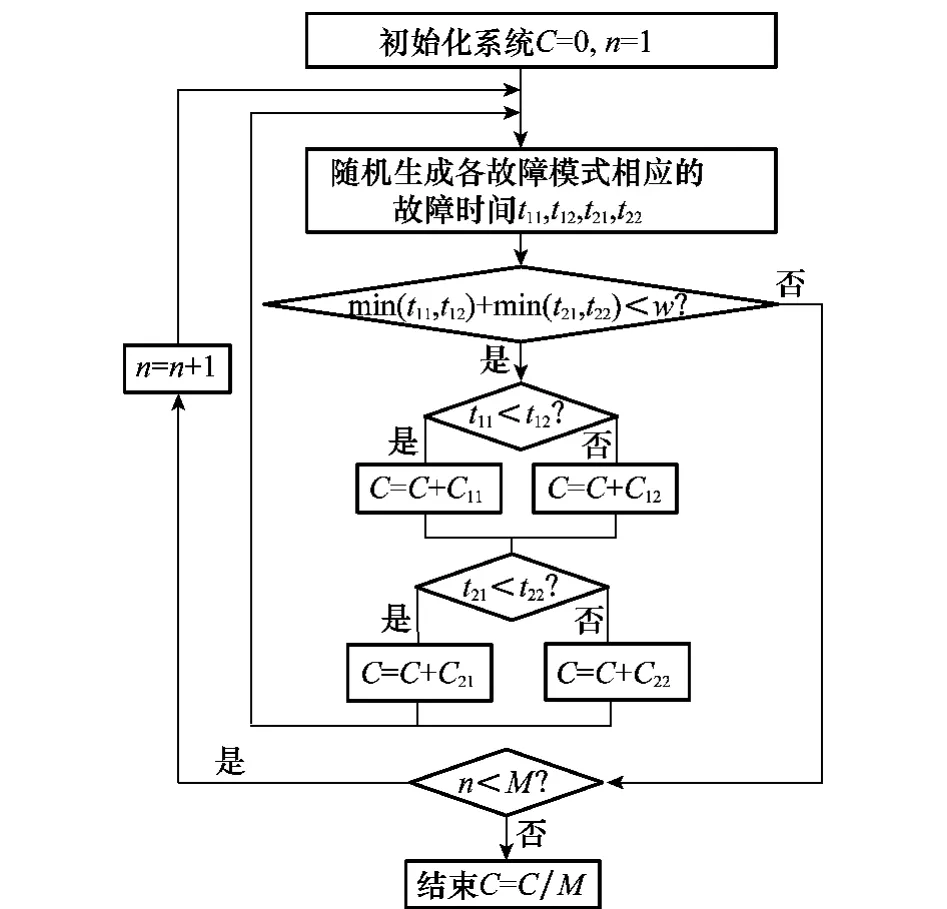
圖6 基于蒙特卡羅法的更新保修費用仿真流程

圖6中，C為保修費用，n為仿真次數(shù)，設(shè)為100次。t11、t12、t21和t22為通過仿真得到故障模式FM11、FM12、FM21和FM22發(fā)生時間。模型數(shù)據(jù)和仿真數(shù)據(jù)對比如圖7所示。

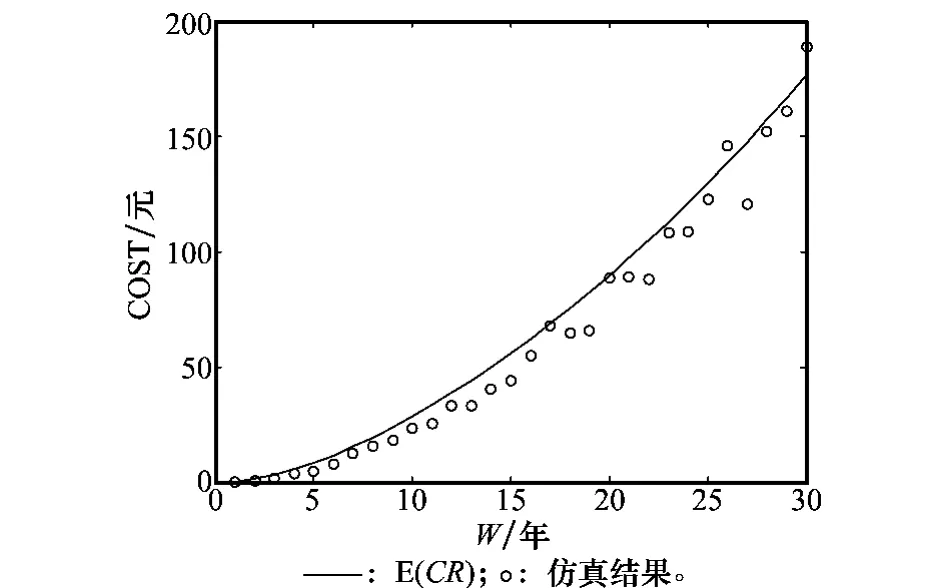
圖7 保修期望費用和保修仿真費用

從圖7中可以看出，仿真值和計算值擬合程度較好，驗證了模型的有效性。其中，保修費用期望、費用標準差、變異系數(shù)和仿真數(shù)值部分數(shù)據(jù)比較如表2所示。變異系數(shù)為，用來衡量計算值隨著時間推移變異程度的變化情況。費用變異系數(shù)和系統(tǒng)可靠性如圖8所示。由圖8中費用的變異系數(shù)的變化趨勢可以看出，隨著保修期W 增加，保修費用變化不太明顯，這是因為當保修期達到一定數(shù)值后，保修終止的可能性變小。

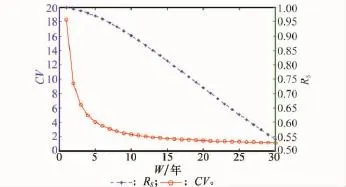
圖8 CV和系統(tǒng)可靠性Rs

利用仿真值，對模型費用計算效果進行絕對誤差分析和相對誤差分析。絕對誤差指標采用均方根誤差（root mean square error，RMSE）、平均絕對誤差（mean absolute error，MAE）和方差絕對誤差（absolute error of absolute，VAE），而相對誤差指標選用平均相對誤差（mean average relative error，MARE）和方差相對誤差（variance relative error，VRE）。各指標具體計算公式如下，具體數(shù)值結(jié)果如表3所示。

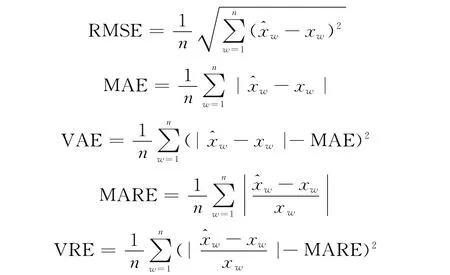
式中，xw表示更新保修費用仿真值表示更新保修期望費用。指標值越小，表示預(yù)測的精度越高。下面以單元1的故障模式FM11和單元2的故障模式FM21為代表，對模型進行敏感性分析，如圖9和圖10所示。從圖中可以看出，E（CR）隨著故障模式的故障率增加而增加。比較圖9和圖10可以發(fā)現(xiàn)，該系統(tǒng)第二個單元故障率的變化對費用的影響較大。因此，在儲備過程中，適當提高儲備單元的可靠性可以有效降低系統(tǒng)的更新保修費用。本案例的研究結(jié)果，可以輔助承制單位計算更新保修費用，也可以幫助軍方衡量保修費用是否合理。當承制單位根據(jù)自身戰(zhàn)略方案選擇合理保修年限時，可以通過權(quán)衡保修費用確定合理的裝備價格，與軍方快速達到價格共識，加快軍民融合速度。

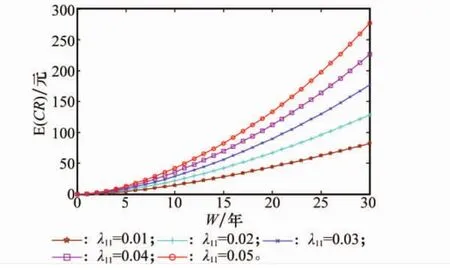
圖9 E（CR）隨λ11變化趨勢

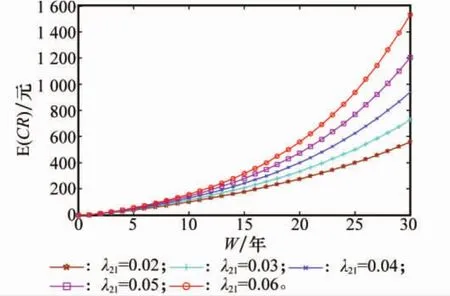
圖10 E（CR）隨λ21變化趨勢

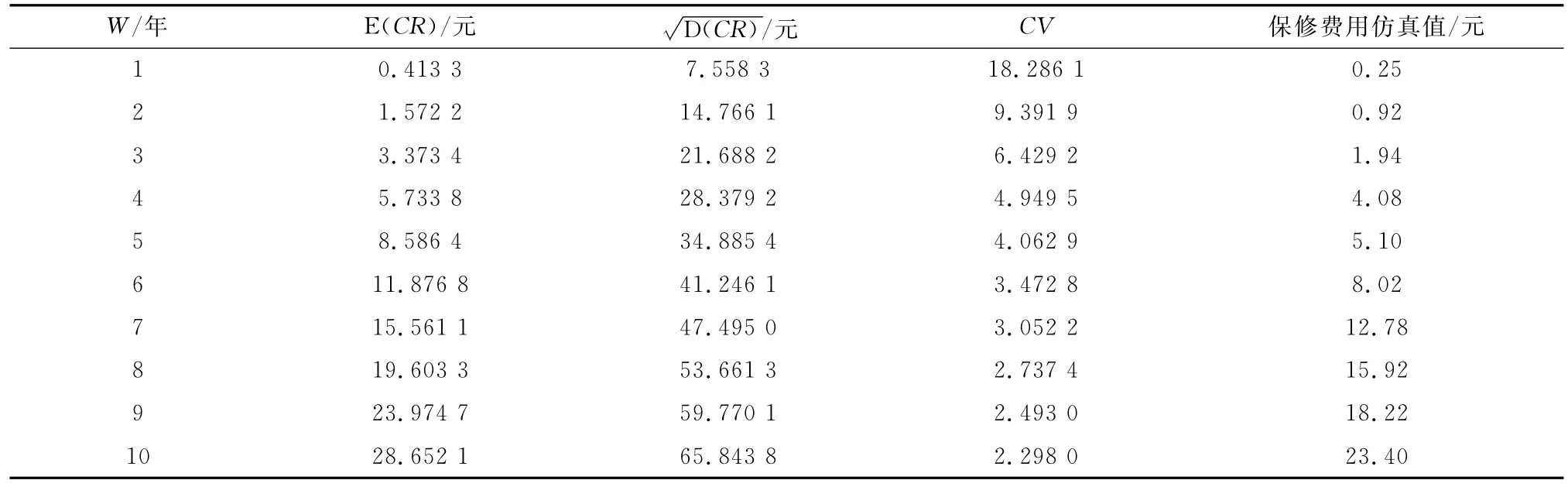
表2 保修費用期望、費用標準差、變異系數(shù)和仿真數(shù)值部分數(shù)據(jù)

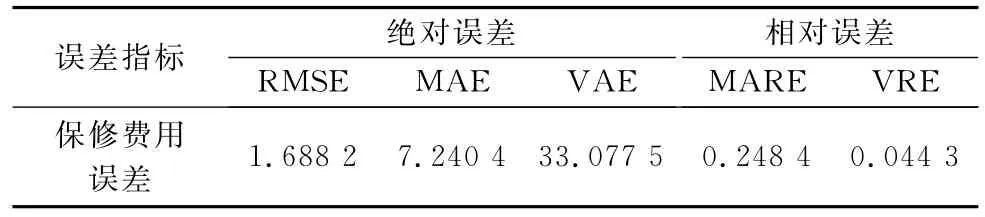
表3 保修期望費用誤差分析

4 結(jié) 論

為推進軍民融合維修保障深度發(fā)展，本文以系統(tǒng)工程理論為指導(dǎo)，首先設(shè)計了保修策略體系。然后在此基礎(chǔ)上，結(jié)合軍方裝備維修保障實際需求，針對更新保修費用難以預(yù)測問題，從單部件和多部件的角度建立了一維多故障模式的更新保修策略費用模型。最后以某冷儲備系統(tǒng)為例，對模型進行了求解計算，并利用蒙特卡羅仿真結(jié)果對比模型計算結(jié)果，進行了誤差分析和敏感性分析，驗證了模型的有效性和實用性。研究成果為更新保修策略在具體裝備中的應(yīng)用提供了理論基礎(chǔ)，為深入推進軍民融合發(fā)展提供了理論支持。雖然筆者對更新保修建模進行了探索，但在未來的研究中還需對模型進行進一步的擴展研究：①考慮不完善維修；②考慮各故障模式相關(guān)時費用預(yù)測問題；③針對冷儲備系統(tǒng)的維修，不是在系統(tǒng)壞了之后統(tǒng)一更換故障單元，而是在系統(tǒng)切換到使用備用單元時就對故障單元進行更換。

［1］Murthy D N P.Product warranty and reliability［J］.Annals of Operations Research，2006，143（1）：133－146.

［2］Yeo W M，Yuan X M.Optimal warranty policies for systems with imperfect repair［J］.European Journal of Operational Research，2009，199（1）：187－197.

［3］Bouguerra S，Chelbi A，Rezg N.A decision model for adopting an extended warranty under different maintenance policies［J］.International Journal of Production Economics，2012，135（2）：840－849.

［4］Blischke W R，Murthy D N P.Product warranty management-I：a taxonomy for warranty policies［J］.European Journal of Operational Research，1992，62（2）：127－148.

［5］Shafiee M，Chukova S.Maintenance models in warranty：a literature review［J］.European Journal of Operational Research，2013，229（3）：561－572.

［6］Blischke W R.Product warranty handbook［M］.Florida：CRC Press，1995：67－180.

［7］Blischke W R.Warranty management and product manufacture［M］.London：Springer，2006：16－127.

［8］Wang L C.Research on warranty period of new equipment based on preventive warranty policy［D］.Shijiazhuang：Ordnance engineering college，2010.（王祿超.預(yù)防性保修策略下的高新裝備保修期研究［D］.石家莊：軍械工程學(xué)院，2010.）

［9］Blischke W R，Murthy D N P.Warranty cost analysis［M］.Florida：CRC Press，1994：246－312.

［10］Huang Y S，Zhuo Y F.Estimation of future breakdowns to determine optimal warranty policies for products with deterioration［J］.Reliability Engineering ＆System Safety，2004，84（2）：163－168.

［11］Chukova S，Aronold R，Wang D Q.Warranty analysis：an approach to modeling imperfect repairs［J］.International Journal of Production Economics，2004，89（1）：57－68.

［12］Su C，Shen J.Analysis of extended warranty policies with different repair options［J］.Engineering Failure Analysis，2012（25）：49－62.

［13］Bai J，Pham H.Cost analysis on renewable full-service warranties for multi-component system［J］.European Journal of Operational Research，2006，168（2）：492－508.

［14］Park M，Pham H.Altered quasi-renewal concepts for modeling renewable warranty costs with imperfect repairs［J］.Mathematical and Computer Modeling，2010，52（9）：1435－1450.

［15］Wu S，Longhurst P.Optimising age-replacement and extended nonrenewing warranty policies in lifecycle costing［J］.International Journal of Production Economics，2011，130（2）：262－267.

［16］Bai J，Pham H.Repair-limit risk-free warranty policies with imperfect repair［J］.IEEE Trans.on System，Man，and Cybernetics—Part A：System and Humans，2005，35（6）：765－772.

［17］Park M，Pham H.Warranty cost analyses using quasi-renewal processes for multi-component systems［J］.IEEE Trans.on System，Man，and Cybernetics-Part A：System and Humans，2010，40（6）：1329－1340.

［18］Jack N，Iskandar B P，Murthy D N P，A repair-replace strategy based on usage rate for items sold with a two-dimensional warranty［J］.Reliability Engineering ＆System Safety，2009，94（2）：611－617.

［19］Park M，Pham H.A new warranty policy with failure times and warranty servicing times［J］.IEEE Trans.on Reliability，2012，61（3）：822－831.

［20］Chukova S，Johnston M R.Two-dimensional warranty repair strategy based on minimal and complete repairs［J］.Mathemat-ical and Computer Modeling，2006，44（11）：1133－1143.

［21］Chen T，Popova E.Maintenance policies with two-dimensional warranty［J］.Reliability Engineering ＆System Safety，2002，77（1）：61－69.

［22］Varnosafaderani S，Chukova S.A two-dimensional warranty servicing strategy based on reduction in product failure intensity［J］.Computers＆Mathematics with Applications，2012，63（1）：201－213.

［23］Chien Y H.The effect of a pro-rata rebate warranty on the age replacement policy with salvage value consideration［J］.IEEE Trans.on Reliability，2010，59（2）：383－392.

［24］Li X Y，Jia Y X，Han Y C，et al.Study on the warranty mode for the new-tech equipment under the condition of military-civil integration［J］.Journal of Ordnance Engineering College，2014，26（3）：15－20.）（李欣玥，賈云獻，韓玉成，等.軍民融合條件下新型軍械裝備保修模式研究［J］.軍械工程學(xué)院學(xué)報，2014，26（3）：15－20.）

［25］Wang W，Banjevic D，Pecht M.A muti-component and multi-failure mode inspection model based on the delay time concept［J］.Reliability Engineering ＆System Safety，2010，95（8）：912－920.

李欣玥（1987－），通信作者，女，博士研究生，主要研究方向為裝備保障理論與應(yīng)用、裝備維修工程。

E-mail：oeclxy＠hotmail.com

王 鵬（1968－），男，工程師，博士，主要研究方向為可維修系統(tǒng)建模、失效預(yù)測、基于退化的系統(tǒng)可靠性分析。

E-mail：pengwang2005＠yahoo.com

鄒 效（1987－），男，助理工程師，碩士研究生，主要研究方向為裝備保障理論與應(yīng)用、裝備維修工程。

E-mail：zouxiao1987zx＠163.com

Cost prediction of the renewing warranty policy considering multiple failure modes for new equipment

JIA Yun-xian1，LI Xin-yue1，WANG Peng2，ZOU Xiao1
（1.Department of Equipment Command and Management，Ordnance Engineering College，Shijiazhuang 050003，China；2.Reliability department，Pratt ＆Whitney，San Diego 92130，USA）

According to the actual requirements of the army maintenance support，a warranty policy system was formulated.Then，aiming at the difficulty of predicting the renewing warranty cost，a cost model for the one-dimensional renewing free-repair warranty policy is proposed considering the reality of the equipment’s multiple failure modes.Multiple failure modes cost models for series，parallel，compound，and cold-standby systems are developed.Finally，a case study，taking certain cold standby system for example，is shown to prove that the proposed models are effective and practical.The results of this method could provide theoretic guidance and technical support to construct the equipment maintenance support under the condition of military-civil integration.

multiple failure mode；multi-component；renewing warranty；cost model

E 92；F 403.8

A

10.3969／j.issn.1001-506X.2015.08.15

賈云獻（1963－），男，教授，博士，主要研究方向為裝備保障理論與應(yīng)用、裝備維修工程。

E-mail：yunxian＿jia＠hotmail.com

1001－506X201508－1810－08

網(wǎng)址：www.sys－ele.com

2014－10－10；

2015－03－18；網(wǎng)絡(luò)優(yōu)先出版日期：2015－04－27。

網(wǎng)絡(luò)優(yōu)先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150427.1635.002.html

國家自然科學(xué)基金（71401173）；國家社科基金軍事學(xué)項目（12GJ003－135）資助課題