混雜系統粒子濾波混合狀態估計及故障診斷算法

郭健彬，紀丁菲，王 鑫，曾聲奎，趙健宇

（1.北京航空航天大學可靠性與系統工程學院，北京100191；2.可靠性與環境工程技術重點實驗室，北京100191；3.電磁散射重點實驗室，北京100854）

混雜系統粒子濾波混合狀態估計及故障診斷算法

郭健彬1，2，紀丁菲1，王 鑫3，曾聲奎1，2，趙健宇1

（1.北京航空航天大學可靠性與系統工程學院，北京100191；2.可靠性與環境工程技術重點實驗室，北京100191；3.電磁散射重點實驗室，北京100854）

混雜系統同時包含連續動態特性和離散動態特性，并且兩種動態相互作用，使其故障診斷變得更加困難。針對此問題，提出了一種混合系統粒子濾波混合狀態估計及故障診斷算法，提高了現有方法的適用范圍和診斷效率。針對混雜系統受控遷移、自治遷移和隨機遷移等特點，首先利用隨機混雜自動機對系統離散狀態（包括故障）和連續狀態進行統一建模，重點對現有基于擴展卡爾曼粒子濾波的連續估計算法進行改進，支持利用在線監測數據來估計混雜系統各類遷移產生的各種離散和連續狀態，最后根據離散狀態估計結果快速實現故障診斷。通過對典型非線性混雜系統的故障診斷，證明了該方法的有效性。

混雜系統；故障診斷；混合狀態估計；擴展卡爾曼粒子濾波

0 引 言

混雜系統（hybrid system，HS）是由連續變量系統和離散事件系統相互作用而構成的一類動態系統，是控制理論和計算機技術等學科交叉而形成的新興分支［1］。混雜系統的離散狀態和連續狀態相互作用使得系統故障行為更加復雜，給故障建模、檢測和定位研究帶來了新的挑戰。傳統故障診斷技術研究主要針對連續系統或離散系統［2－3］，而混雜系統的故障診斷則必須解決離散動態與連續動態的耦合影響，已成為故障診斷領域的一個熱點研究方向。

對混雜系統故障診斷的研究主要有兩個分支。第一分支是殘差檢測方法，假設系統離散狀態可在線監測，在已知當前離散狀態的前提下，通過跟蹤檢測連續變量的偏差來判斷是否發生故障，通過神經網絡等智能算法來進行故障隔離。文獻［4］提出使用混雜自動機（hybrid automation，HA）來描述混雜系統，通過判斷殘差和閾值的關系來診斷嵌入式系統的故障狀況。文獻［5］針對具有未知模式的混合系統提出一種根據混合差分進化算法來對故障定位的方法。文獻［6］研究了從一系列不精確的殘差中提取合適的數據完成故障診斷。

另一分支是混合狀態估計方法，主要針對連續動態系統，將故障視為連續系統中一類特殊的離散事件，通過估計系統的離散狀態從而直接進行故障隔離［7－8］。文獻［9］提出使用隨機混雜自動機（stochastic hybrid automation，SHA）和卡爾曼濾波器來實現故障診斷和狀態估計。文獻［10］利用動態歷史值改進粒子權重的確定方法來提高故障狀態估計的準確性。文獻［11］在隨機混雜自動機的基礎上應用逐段決定馬爾可夫過程來刻畫混雜系統。文獻［12］利用對數似然比改進粒子濾波算法來實現對自治遷移的混雜動力系統故障初始時刻的診斷。

第一類殘差檢測方法只能用于離散狀態可在線監測的混合系統，在此前提下只需對連續特征進行殘差檢測，回避了離散和連續相互作用的難點。第二類混合估計方法可以直接得到系統的故障狀態，故障隔離簡單，但需要考慮離散和連續的耦合效應進行狀態估計，算法比較復雜；而且現有算法只適用于連續系統，即只考慮故障事件這類隨機遷移，無法估計混雜系統由受控遷移、自治遷移產生的離散狀態。

擴展卡爾曼粒子濾波算法（extended Kalman particle filter，EKPF）和隨機混雜自動機技術，提出適用于混雜系統的混合估計和故障診斷算法，可處理混雜系統自身的受控遷移、自治遷移等，將混合估計的適用范圍由連續系統擴展到混雜系統。

1 問題描述

1.1 基于隨機混雜自動機的故障診斷模型

隨機混雜自動機［13－14］可以用一個六元組〈S，X，Y，T，F，H〉來表示。其中，有限集S表示離散狀態空間，X表示系統連續狀態空間，Y表示系統輸出空間，T是離散狀態之間的遷移函數，F是狀態方程的集合，H是觀測方程的集合。隨機混雜自動機包含系統中各種離散狀態、每一離散狀態的連續動態特性，以及各種離散狀態之間的變遷規則，包括受控遷移、自治遷移和隨機遷移。受控遷移即由控制指令引起的轉變，自治遷移即連續變量的變化導致系統自動的轉變，這兩者都屬于由模型本身引起的切換；隨機遷移即引起系統部件故障等不可預期的行為，它屬于外部行為。

本文用SHA來對混雜系統故障過程進行建模，為后續的混合估計提供支撐。在離散狀態S中既考慮了故障狀態，又考慮了混雜系統的正常運行狀態，在狀態遷移函數T中根據故障率來進行隨機遷移，根據控制指令來進行受控遷移，根據變量的閾值條件來進行自治遷移，并且考慮了過程噪聲和測量噪聲，得到基于隨機混雜自動機的故障診斷模型。其示意圖如圖1所示。

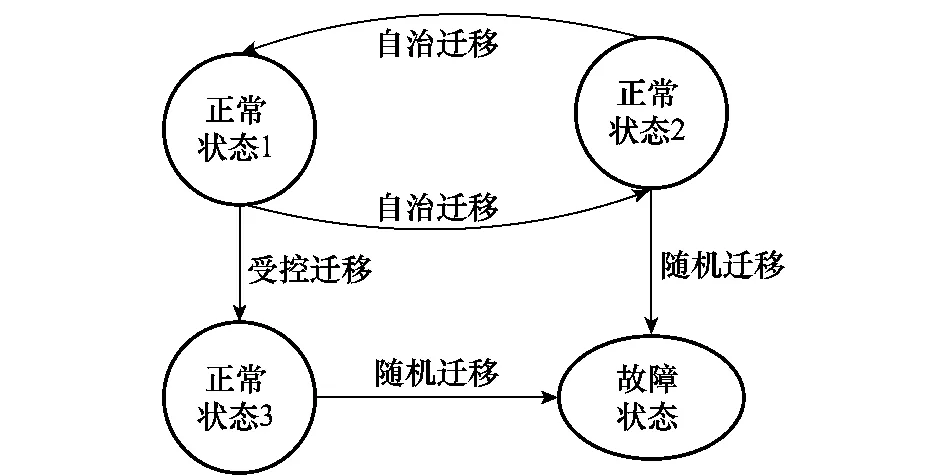
圖1 隨機混雜自動機模型示意圖

當系統處于離散狀態st時，其動態特性可以描述為下面的狀態空間方程

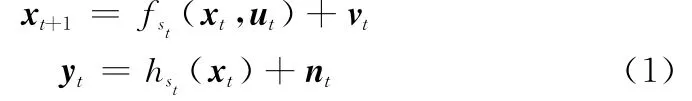
式中，xt是系統的連續狀態向量，st是系統的離散模態，二者合稱為混雜狀態，表示為（st，xt）；yt是連續狀態的觀測值；ut是系統的輸入向量；fst表示離散狀態st對應的系統方程；hst表示相應的觀測方程；vt和nt分別為均值為零、方差為Q和R且相互獨立的過程噪聲和測量噪聲。

1.2 基于混合估計的故障診斷

故障診斷的基本流程如圖2所示：給定初始條件和控制條件，由系統混雜自動機模型得到輸出的觀測值；然后根據觀測值由濾波器進行混合估計，得到連續狀態變量和離散狀態變量的估計值；最后依據離散狀態估計值即可快速推斷出混雜系統發生的故障。

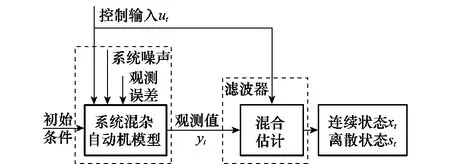
圖2 基于混合估計的故障診斷流程

基于上述隨機混雜自動機模型，將故障診斷轉換成離散狀態估計問題，根據估計得到的離散狀態即可判斷系統是否故障，以及處于哪一種故障狀況下。因此，可以把這類故障診斷問題表述為：在給定混雜系統的模型下，利用觀測序列yt＝（y0，y1，…，yt），以及控制序列ut＝（u0，u1，…，ut），估計不可觀測的離散狀態st＝（s0，s1，…，st）。

但是，混雜系統連續狀態與離散狀態相互作用，要實現系統連續狀態的估計則需要考慮離散狀態，反之，要實現離散狀態估計就需要考慮系統連續狀態。由于兩類信息之間存在動態交互，必須利用混合狀態估計來判斷系統所處的狀態。

2 基于擴展卡爾曼粒子濾波的混合狀態估計算法

粒子濾波算法（particle filter，PF）以蒙特卡羅抽樣為基礎，利用隨機狀態粒子集近似后驗概率分布，通過貝葉斯方法遞推更新。文獻［7－9，16］將其用于狀態估計，但存在算法本身性能上的不足，并且只是針對連續系統。EKPF［17－18］就是用擴展卡爾曼濾波來生成重要密度函數，使得PF的先驗分布保持在高似然區域，從而在一定程度上緩解了粒子退化現象，提高了蒙特卡羅的效率以及算法的估計精度，而且適用于非線性系統。

論文以混雜系統混合估計和診斷為目標，改進現有EKPF算法，提出了擴展卡爾曼粒子濾波混合估計算法，一方面支持同時對連續和離散兩類變量進行濾波估計，并且考慮了混雜系統的受控遷移、自治遷移和隨機遷移；另一方面，利用EKPF算法性能上的優勢，提高對非線性混雜系統的診斷效率。擴展卡爾曼粒子濾波混合估計算法流程如圖3所示。

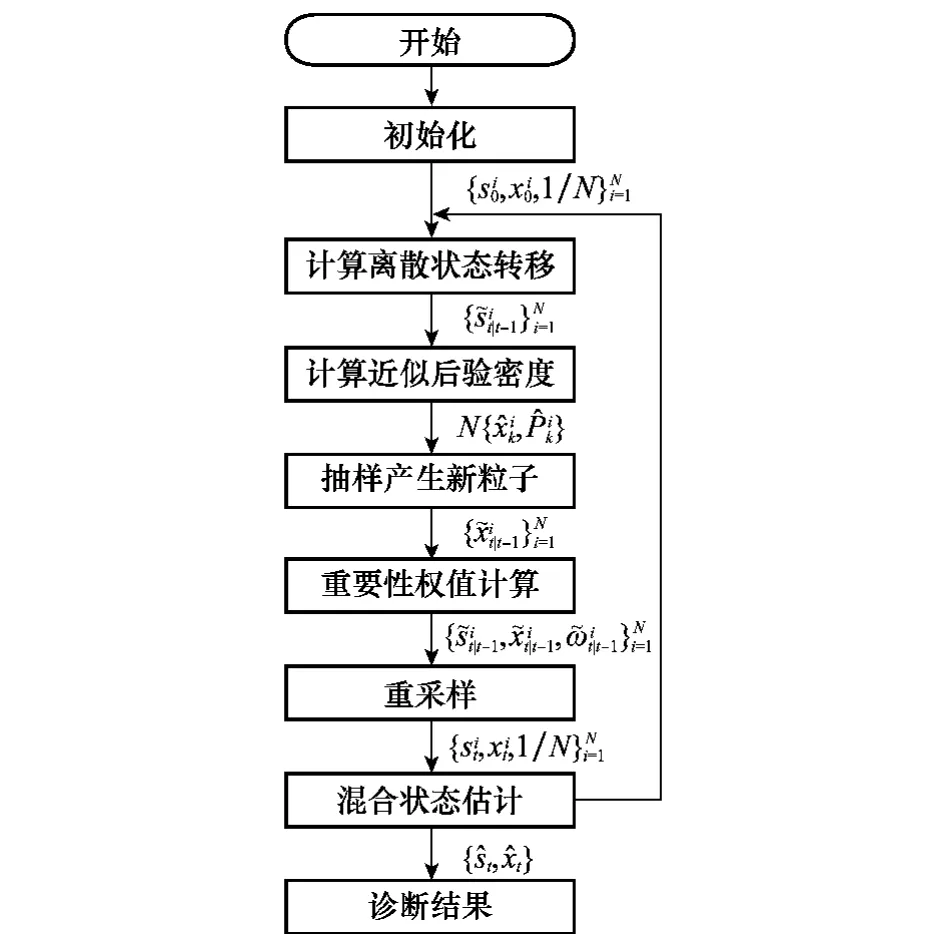
圖3 算法流程示意圖

具體的混合估計和診斷算法如下：

步驟1 初始化

首先利用先驗分布產生一組包含連續狀態和離散狀態的PF初始粒子集合，此集合中每一個樣本具有等加權值。即對于i＝1，2，…，N，從系統的先驗概率p（s0）、p（x0）抽樣等加權樣本集｛si0，xi0，1／N｝Ni＝1，N是粒子個數。

步驟2 計算離散狀態轉移

本文考慮的離散狀態遷移包括3種，一種是收到外界控制指令，即根據u來進行狀態遷移；一種是系統自身的連續狀態達到一定條件自動發生轉移，即變量x達到一定的閾值后發生狀態遷移；一種是用概率描述的故障這種隨機事件，即由故障概率p來進行隨機抽樣決定下一時刻狀態。離散狀態轉移如圖4所示。

步驟3 計算近似后驗密度

結合最新測量信息，通過高斯過程不斷迭代計算更新后驗分布。在PF計算過程中，每個粒子通過EKF更新狀態，就可以得到近似的后驗密度函數［19］。

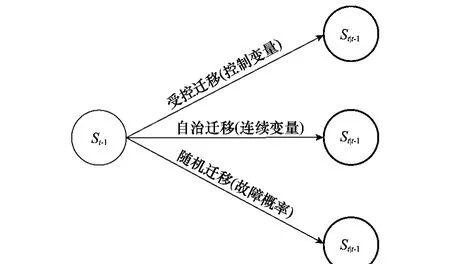
圖4 離散狀態轉移示意圖

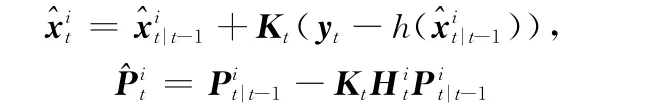
步驟4 抽樣產生新粒子

步驟5 計算重要性權值

根據測量值對樣本進行評估，賦予與之相稱的加權值。

即將測量值與每一樣本的預測比較，根據貝葉斯理論計算加權值得到樣本集并歸一化重要性權值

步驟6 進行重采樣

將上述加權值作為參考進行重采樣，即根據粒子狀態與所觀察信息相符的程度來增減對應的粒子，得到新的等加權值樣本集，作為下一輪迭代的初始樣本集合。從粒子集中根據重要性權值的大小重采樣得到新的N個等加權值粒子，即通過重采樣可以去掉權重較小的粒子，復制權重較大的粒子，提高蒙特卡羅方法的效率。重采樣方法可以采用多項式重采樣、殘差重采樣、最小方差重采樣等［20－21］。

步驟7 混合估計

重復以上遞推過程，粒子集合的近似分布逐漸趨近真實分布。這樣，樣本集中數目最多的離散狀態就作為系統離散狀態估計，同時得到相應的連續狀態估計，從而實現混雜系統的狀態估計和故障診斷。

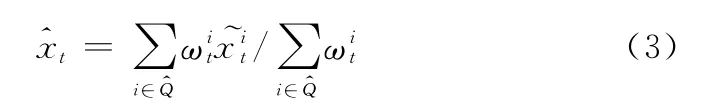
3 案例仿真

3.1 溫度控制系統

溫度控制系統具有多種控制模式和故障狀態，是典型的混雜系統。其離散化后的狀態空間方程如下：

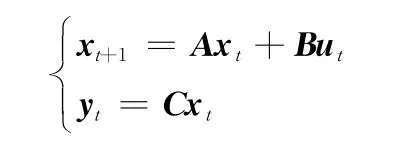
其中

該動態方程表示系統運行的正常狀態。ut≠0時系統處于升溫狀態，離散狀態st＝1；ut＝0時系統處于降溫狀態，離散狀態，st＝2；且當x2＞75時，系統發生自治變遷令ut＝0；升溫由人為控制。故障的發生為隨機變遷。考慮系統的傳感器故障和噪聲后的系統的狀態方程如下：

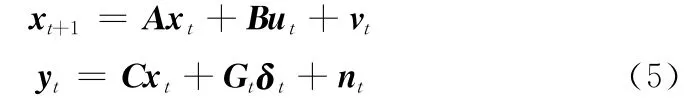
式中，vt為過程噪聲，nt為測量噪聲，它們都是零均值高斯白噪聲，設其協方差均為0.01；δt為傳感器故障函數（恒增益故障），設δt＝［10；100］T；Gt為對角陣，Gt＝［1，0；0，0］T時，表示傳感器1發生故障；Gt＝［0，0；0，1］T時，表示傳感器2發生故障。

該系統的隨機混雜自動機模型如圖5所示。圖中st＝1和st＝2表示系統的兩個正常運行狀態，兩者之間可以相互轉換。其余的4個狀態表示故障狀態。st＝3表示系統在升溫（st＝1）時發生傳感器1故障后的狀態；st＝4表示系統在降溫（st＝2）時發生傳感器1故障后的狀態；以此類推。假設兩個故障發生的概率均為0.002，且發生故障后系統狀態不可逆轉。

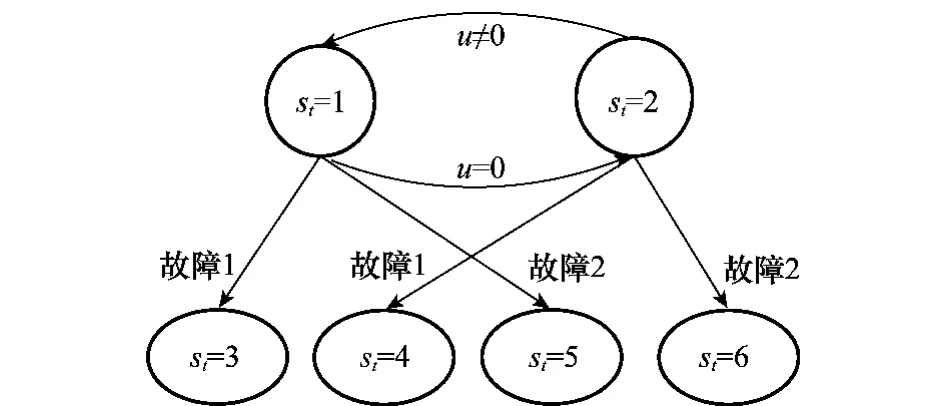
圖5 系統混雜自動機模型示意圖

仿真設定如下：初始離散狀態s0＝1，連續狀態x0＝［1 1 1 1］T；當t＝800k（k為步長）時，系統發生故障1；粒子數為200。仿真結果如圖6和圖7所示。

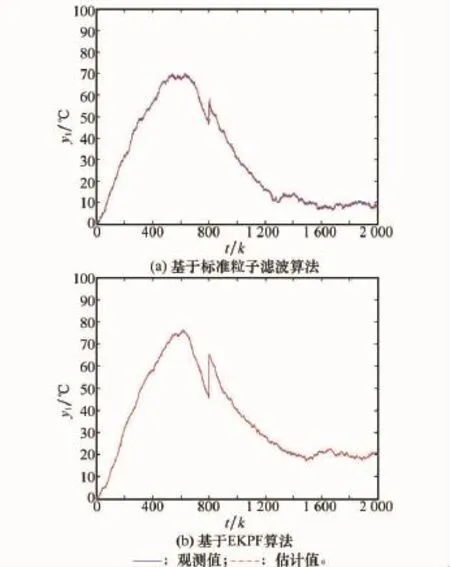
圖6 連續狀態估計結果

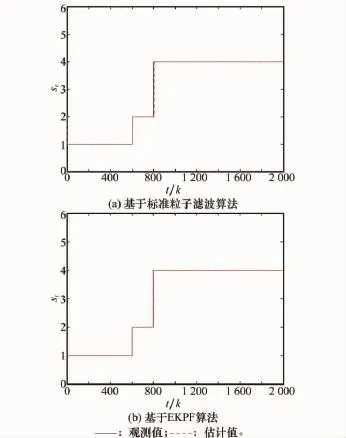
圖7 離散狀態估計結果

由圖6和圖7可以看出，基于EKPF的混合估計算法能對混雜系統的狀態進行實時監控。由圖7的估計值可以判斷出，在t＝809k時系統離散狀態跳變為st＝4，結合圖5系統混雜自動機模型，可以診斷出系統發生了傳感器1故障，即表明該算法能夠實現實時診斷，相比于基于標準粒子濾波的混合估計算法跟蹤性能較好，故障診斷更快速。

3.2 非線性系統

下面采用一個160MW燃油機組的動態模型為對象來驗證算法［22］。該模型的離散方程如下：

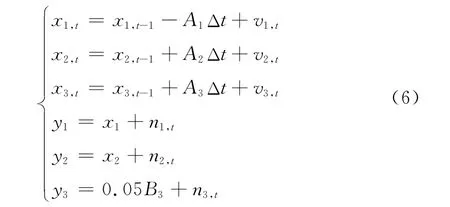
其中，相關量定義如下：

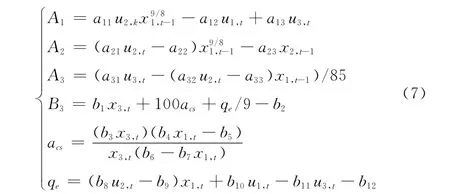
式中，x1為汽包壓力；x2為輸出功率；x3汽包液體密度；u1為燃油調節閥開度；u2為汽輪機調節閥開度；u3為給水調節閥開度；y3汽包水位；vt為過程噪聲，nt為測量噪聲，它們都是零均值高斯白噪聲，設其協方差均為0.01。這個動態方程表示系統運行的正常模式。ut＝［0.3 0.4 0.5］時系統的離散狀態st＝1，ut＝［0.4 0.9 0.5］時系統的離散狀態st＝2。

考慮汽包水位傳感器，假設該系統的傳感器有以下3種故障模式：

（1）恒偏差故障，y3，t＝0.05B3＋2＋n3，t；

（2）恒增益故障，y3，t＝0.1B3＋n3，t；

（3）卡死故障，y3，t＝0＋n3，t。

該系統的隨機混雜自動機模型示意圖如圖8所示。圖中st＝1和st＝2表示系統的兩個正常運行模式，兩者之間可以相互轉換。其余的6個狀態表示故障狀態。st＝3表示系統在st＝1時發生故障1后的狀態；st＝4表示系統在st＝1時發生故障2后的狀態；以此類推。假設3個故障發生的概率均為0.002，且發生故障后系統模式不可逆轉。

仿真設定如下：當1s≤t≤100s時，系統處于狀態1；當100s≤t≤200s時，系統處于狀態2；在t＝200s時注入故障2，當200s≤t≤300s時，系統處于狀態7。設置初始狀態s0＝1，初始狀態x0＝［108 66.65 428］T，離散步長為0.01s，粒子數為500，傳感器采樣頻率為1Hz，其余參數為：a11＝0.001 8，a12＝0.9，a13＝0.15，a21＝0.073，a22＝0.016，a23＝0.1，a31＝141，a32＝1.1，a33＝0.19，b1＝0.131，b2＝0.068，b3＝0.001 54，b4＝0.8，b5＝25.6，b6＝1.039 4，b7＝0.001 23，b8＝0.854，b9＝0.147，b10＝45.59，b11＝2.514，b12＝2.096。

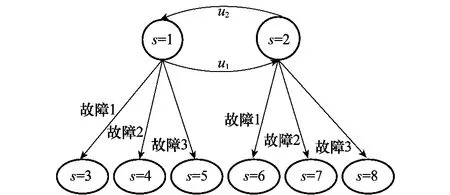
圖8 系統混雜自動機模型示意圖

利用本文所提出的算法，仿真結果如圖9和圖10所示。由輸出估計結果圖9可以看出，基于EKPF的混合估計算法能對混雜系統的狀態進行實時監控。由離散狀態估計結果圖10可以看出，在t＝100s時系統離散狀態跳變為st＝7，結合系統混雜自動機模型，可以診斷出系統發生了故障2。這表明該算法能夠實現實時診斷，且對非線性系統的狀態估計準確，跟蹤效率較高。而標準粒子濾波算法則給出了錯誤的診斷結果。

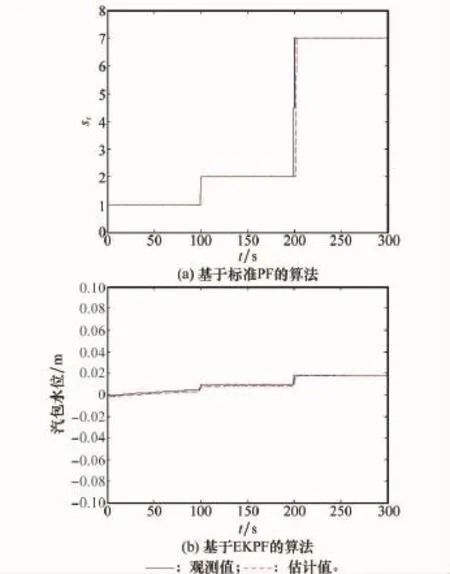
圖9 連續狀態估計結果（本文算法）

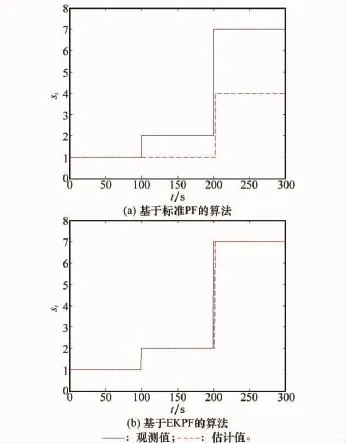
圖10 離散狀態估計結果（本文算法）

4 結束語

傳統混合估計算法只能對連續系統進行故障診斷，并且對非線性系統的診斷效率偏低。本文針對混雜系統具有的受控遷移、自治遷移和隨機遷移，提出了擴展卡爾曼粒子濾波混合估計和診斷算法，通過案例可以證明該方法能夠同時跟蹤非線性混雜系統的離散狀態和連續狀態，并快速給出診斷結果。

案例結果表明，本算法雖然實現過程相對復雜，但診斷快速性和跟蹤性較好，對非線性較強的系統也具有較好的魯棒性。

對于高維混雜系統，由于粒子濾波算法的計算量明顯增大。后續的研究中還需要設計更高效的混合估計算法，如粒子群優化粒子濾波等智能算法。

［1］Arjan V D S，Hans S.An introduction to hybrid dynamical systems［M］.London：Springer，2000：1－9.

［2］Fan S，Chai X D，Li T.Knowledge handling methods in qualitative ＆quantitative fault diagnosis platform［J］.Computer Integrated Manufacturing Systems，2010，16（10）：2166－2173.（范帥，柴旭東，李潭.定性定量故障診斷平臺中的知識處理方法［J］.計算機集成制造系統，2010，16（10）：2166－2173.）

［3］Han G C，Sun S D，Si S B，et al.Research on fault diagnosis simulation based on fuzzy probability Petri nets system［J］.Computer Integrated Manufacturing Systems，2006，12（4）：520－525.（韓光臣，孫樹棟，司書賓，等.基于模糊概率Petri網系統的故障診斷仿真研究［J］.計算機集成制造系統，2006，12（4）：520－525.）

［4］Koutsoukos X，Zhao F，Haussecker H，et al.Fault modeling for monitoring and diagnosis of sensor-rich hybrid systems［C］∥Proc.of the 40th IEEE Conference on Decision and Control，2001：793－801.

［5］Yu M，Wang D W，Huang L.Incipient fault diagnosis and prognosis for hybrid systems with unknown mode changes［C］∥Proc.of the Prognostics ＆System Health Management Conference，2010：1－7.

［6］Mohammadi R，Hashtrudi-Zad S，Khorasani K.Diagnosis of hybrid systems：part 2-residual generator selection and diagnosis in the presence of unreliable residual generators［C］∥Proc.of the IEEE International Conference on Systems，Man，and Cybernetics，2009：3340－3345.

［7］Siamak T，Sun X H.Hybrid system state tracking and fault detection using particle filters［J］.IEEE Trans.on Control Systems Technology，2006，14（6）：1078－1087.

［8］Liu Y T，Jiang J P.Fault diagnosis and prediction of hybrid system based on particle filter algorithm［C］∥Proc.of the IEEE International Conference on Automation and Logistics，2008：1491－1495.

［9］Michael W H，Brian C W.Mode estimation of probabilistic hybrid systems［C］∥Proc.of the Hybrid Systems：Computation and Control，2002：263－266.

［10］Salahshoor K，Samadi M F，Safari E.Particle filtering mode estimation of hybrid systems based on a novel weighted mode activation record approach［C］∥Proc.of the IEEE International Conference on Control and Automation，2009：430－434.

［11］Zhang H，Dufour F，Dutuit Y，et al.Piecewise deterministic Markov processes and dynamic reliability［C］∥Proc.of the Institution of Mechanical Engineers，Part O：Journal of Risk and Reliability，2008，222（4）：545－551.

［12］Cadini F，Zio E，Peloni G.Particle filtering for the detection of fault onset time in hybrid dynamic systems with autonomous transitions［J］.IEEE Trans.on Reliability，2012，61（1）：130－139.

［13］Perez Castaneda G A，Aubry J F，Brinzel N.Stochastic hybrid automata model for dynamic reliability assessment［C］∥Proc.of the Institution of Mechanical Engineers，Part O：Journal of Risk and Reliability，2011：28－41.

［14］Wang X，Guo J B.The method of system reliability modeling based on hybrid theory［C］∥Proc.of the 9th International Conference on Reliability，Maintainability and Safety，2011：199－207.

［15］Guo J B，Du S H，Wang X，et al.Fault hybrid propagation and modeling method for dynamic system［J］.Systems Engineering and Electronics，2015，37（1）：224－228.（郭健彬，杜紹華，王鑫，等.動態系統故障的混雜傳播特征及建模方法［J］.系統工程與電子技術，2015，37（1）：224－228.）

［16］Yu J.A particle filter driven dynamic Gaussian mixture model approach for complex process monitoring and fault diagnosis［J］.Journal of Process Control，2012，22（4）：778－788.

［17］Wu P，Kong J，Bo Y.Modified iterated extended Kalman particle filter for single satellite passive tracking［J］.Turkish Journal of Electrical Engineering ＆Computer Sciences，2013，21（1）：120－130.

［18］Lee S H，West M.Performance comparison of the distributed extended Kalman filter and Markov chain distributed particle filter（MCDPF）［C］∥Proc.of the 2nd IFAC Workshop on Distributed Estimation and Control in Networked Systems，2010：151－156.

［19］Prakash J，Patwardhan S C，Shah S L.On the choice of importance distributions for unconstrained and constrained state estimation using particle filter［J］.Journal of Process Control，2011，21（1）：3－16.

［20］Gustafsson F.Particle filter theory and practice with positioning applications［J］.Aerospace and Electronic Systems Magazine，2010，25（7）：53－82.

［21］Zhao L.Nonlinear system filtering theory［M］.Beijing：National Defense Industry Press，2012：147－148.（趙琳.非線性系統濾波理論［M］.北京：國防工業出版社，2012：147－148.）

［22］Zhu Z Y.The particle filtering algorithm and application［M］.Beijing：Science Press，2010：185－189.（朱志宇.粒子濾波算法及其應用［M］.北京：科學出版社，2010：185－189.）

Hybrid state estimation and fault diagnosis algorithm of hybrid systems using particle filter

GUO Jian-bin1，2，JI Ding-fei1，WANG Xin3，ZENG Sheng-kui1，2，ZHAO Jian-yu1
（1.School of Reliability and Systems Engineering，Beihang University，Beijing 100191，China；2.Science and Technology on Reliability and Environment Engineering Library，Beijing 100191，China；3.Science and Technology on Electromagnetic and Scattering Library，Beijing 100854，China）

Hybrid systems are composed of discrete event dynamic systems and continuous time dynamic systems，which interact with each other.It leads to that the fault diagnosis of hybrid systems is particularly difficult.In order to expand the scope of application and improve the diagnosis efficiency，a hybrid state estimation based hybrid systems fault diagnosis method is proposed.Considering the controlled migration，the autonomous migration and the stochastic migration of hybrid systems，the discrete states（including fault states）and continuous states of the system are modeled based on the stochastic hybrid automaton.The common extended Kalman particle filter based hybrid estimation algorithm is developed so as to be applied in the hybrid estimation of discrete and continuous states produced by the migrations of hybrid systems.Finally，the fault diagnosis can be achieved rapidly according to the estimated result of discrete states.A simulation experiment is employed to conduct the fault diagnosis on a typical nonlinear hybrid system，and the results indicate that this method is effective.

hybrid systems；fault diagnosis；hybrid state estimation；extended Kalman particle filter

TP 206

A

10.3969／j.issn.1001-506X.2015.08.33

郭健彬（1979－），男，講師，博士，主要研究方向為系統可靠性、故障診斷、故障機理、可靠性優化。

E-mail：guojianbin＠buaa.edu.cn

紀丁菲（1987－），女，碩士研究生，主要研究方向為混雜系統故障診斷。

E-mail：wanderfula＠163.com

王 鑫（1985－），男，工程師，碩士，主要研究方向為系統可靠性、混雜系統。

E-mail：w＿xin＿ok＠126.com

曾聲奎（1968－），男，研究員，博士，主要研究方向為系統可靠性、故障機理、可靠性與性能一體化設計。

E-mail：zengshengkui＠buaa.edu.cn

趙健宇（1990－），男，博士研究生，主要研究方向為混雜系統故障診斷。

E-mail：zhaojianyu＠buaa.edu.cn

1001－506X201508－1936－07

網址：www.sys－ele.com

2014－09－03；

2015－01－26；網絡優先出版日期：2015－04－28。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150428.1650.002.html

國家自然科學基金（61304218）；北京市自然科學基金（3153027）資助課題