基于比例失效率退化模型的可靠性評估方法

蔡忠義，陳云翔，張諍敏，項華春

（空軍工程大學裝備管理與安全工程學院，陜西西安710051）

基于比例失效率退化模型的可靠性評估方法

蔡忠義，陳云翔，張諍敏，項華春

（空軍工程大學裝備管理與安全工程學院，陜西西安710051）

針對不假定壽命分布類型的長壽命可靠性評估問題，提出一種不同于傳統基于退化軌跡和退化量分布的退化數據可靠性評估方法。將時間視為類加速因子并作為協變量，通過引入比例風險模型來描述產品壽命與退化量失效率之間的關系，建立比例失效率退化模型；通過考慮分布簇之間的差異度來確定退化量分布類型，求出退化量基準失效函數及比例失效率系數；采用線性回歸模型擬合出類加速模型參數估計，確定已知檢測時刻下的退化量失效率函數，并外推產品在退化失效閾值下的壽命可靠度函數；結合實例分析，驗證方法的實用性和有效性。

退化數據；可靠性評估；比例風險模型；分布差異度；基準失效率

0 引 言

根據產品喪失功能的形式，失效可分為突發失效和退化失效兩類［1－2］。其中，突發失效是指產品在某時刻功能突然喪失的現象，而退化失效是指產品在使用中功能逐漸下降，直至無法滿足規定要求。對高可靠性產品而言，由于難以獲取足夠多的突發失效數據，使得傳統基于突發失效數據的可靠性評估方法不再適用，而基于性能退化數據的可靠性評估方法卻能很好地解決此類問題。

目前，傳統的退化數據可靠性評估方法主要有兩類［3－4］：一是基于退化軌跡曲線［5－6］。這類方法是在已知產品的退化失效物理模型的基礎上，通過擬合性能退化數據隨時間變化的軌跡曲線來估計可靠度，但對于退化軌跡復雜或不明的產品，其失效過程難以用特定的軌跡模型進行擬合，導致其評估誤差較大。二是基于退化量分布［7－8］。這類方法是假設退化量服從某一已知的分布，通過擬合分布參數隨時間變化的曲線來估計可靠度，由于對退化量分布的假定過于主觀且在工程實際中很難確定退化量服從的具體分布模型，使其適用范圍受到限制。

比例風險模型最初由學者Cox D R提出并應用于壽命數據分析，其優勢是估計不需要依賴于所選的壽命分布［9］。學者Eghbali擴展了Cox的比例風險模型，提出一種融合加速退化因子的比例風險退化模型并用于處理加速退化數據［10－11］。基于加速退化數據的比例風險退化模型是一種非參數估計模型，以應力隨時間的變化為協變量，建立比例風險加速退化模型，適用于分布規律未知的退化失效問題［12－13］。文獻［14－15］將比例風險模型推廣應用于非加速條件下性能退化數據的可靠性評估。其中，文獻［14］以退化量為協變量，假定壽命基準失效率為λ0（t）＝abtb－1，實際是默認產品壽命服從威布爾分布，使得方法缺乏一般適用性。

基于上述考慮，本文針對性能退化參數僅有一個的一元退化失效問題，提出了一種不同于傳統方法的非參數形式下退化數據可靠性評估方法，即不假定產品壽命分布類型，通過考慮分布簇之間的差異度來確定退化量分布類型，將不同檢測時刻視為類加速因子并作為協變量，建立比例失效率退化模型。

1 預備知識

1.1 失效率

已知壽命T的可靠度函數為R（t），其密度函數為f（t），則壽命T的失效率函數（或稱危險函數）表示為

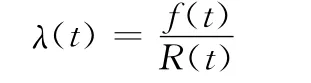
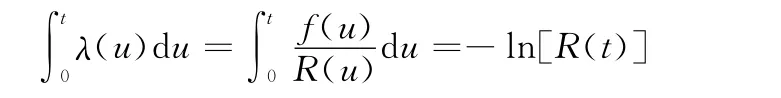
則可靠度與失效率之間的關系式為

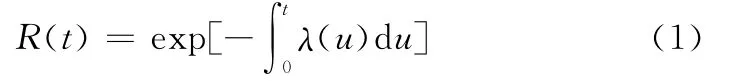
1.2 比例風險模型

已知協變量x下壽命T的可靠度函數為RT（t／x），其密度函數為fT（t／x），則給定x下的壽命T的失效率函數表示為

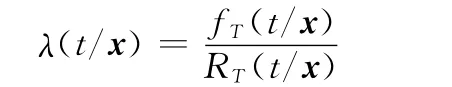
上式兩邊同時對t積分：

若失效率函數具有如下性質：當x1≠x2時，λ（t／x1）／λ（t／x2）與t無關，則認為壽命T與協變量x的關系適用于比例危險模型（proportional hazard model），可表示為

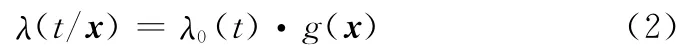
式中，λ0（t）可以理解為g（x）＝1下的基準失效率函數。當g（x）用參數形式表示時，即g（x）＝exp（xβ），則式（2）也稱為COX模型。

2 比例失效率退化建模

2.1 模型假設

（1）產品失效只考慮性能退化失效且性能退化關鍵參數僅有一個，不考慮突發失效，表征產品性能降低的退化量Y（t）是時間t的單調函數。本文假定Y（t）是單調增函數，當退化量大于失效閾值yc時，判定產品失效。

（2）產品性能退化試驗為平衡試驗，即選擇相同的檢測時刻ti（i＝1，2，…，n）對m個試驗產品的退化量進行檢測，共得到n×m個退化數據yij（i＝1，2，…，n；j＝1，2，…，m）。

（3）檢測時刻ti的性能退化數據yi服從于某未知分布，即yi～F（yi，θi）且yiidij～F（yi，θi）（θi為未知參數）。

2.2 退化量分布與壽命分布之間的關系

已知產品的性能退化量為Y（t）＝h（t，θ）（θ為未知參數），則產品達到退化失效閾值yc的壽命T（yc）＝h－1（yc，θ）。記壽命變量T（yc）的分布函數為FT（t／yc），性能退化量Y（t）在t時刻的分布函數為FY（y／t）且Y（t）是t的增函數，可知

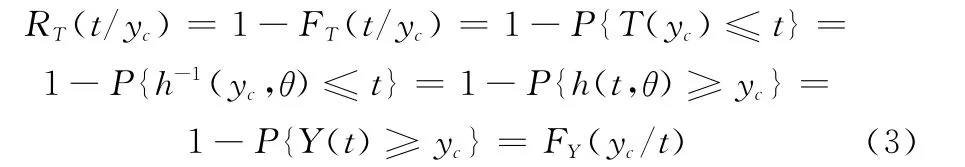
令yc為檢測時刻ti的性能退化值yi（i＝1，2，…，n），則RT（t／yi）＝FY（yi／t）。

2.3 考慮分布差異度的退化量分布確定

對于產品退化量分布模型確定，一般是根據工程實踐經驗，確定其可能服從的某一分布，如正態分布、威布爾分布、對數正態分布、伽瑪分布等。為了充分利用產品性能退化信息，提高退化量分布模型確定的科學性，采用Kullback-Leibler差異來對各可能分布模型之間的差異程度進行度量［8］。

設產品各種可能分布函數組成分布簇Gθ（θ＝（θ1，…，θk）∈Θ）（k為所有可能的分布模型數），確定產品退化量分布函數就是從分布簇Gθ中選擇與其實際退化量分布函數差異最小的分布函數。檢測時刻ti擬選擇的分布函數與該時刻的實際退化量分布函數F（yi，θi）之間的差異程度Δi［Gθ，F（yi，θi）］可表示為

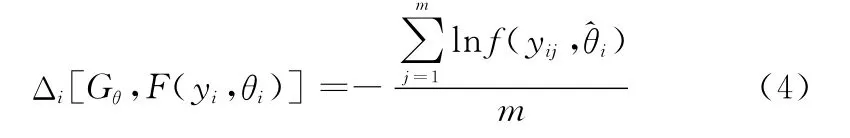
式中，yij為檢測時刻ti上第j個產品退化數據；f（yi，＾θi）為檢測時刻ti上分布模型G＾θ的概率密度函數，＾θi為用檢測時刻ti上的退化數據所得的分布參數估計。

（1）退化數據yi服從正態分布時，其概率密度為

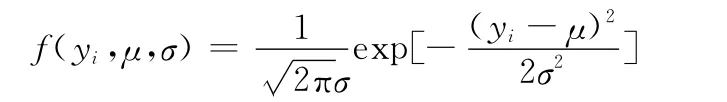
（2）退化數據yi服從對數正態分布時，其概率密度為

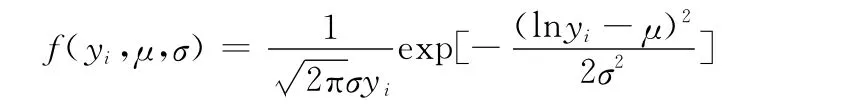
（3）退化數據yi服從威布爾分布（Weibull）時，其概率密度函數為

（4）退化數據yi服從伽瑪分布（Gamma）時，其概率密度函數為

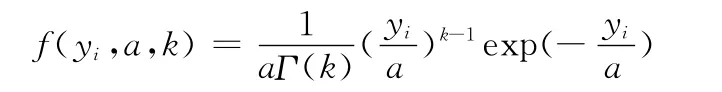
對上述4種分布參數進行估計時，可調用Matlab中的極大似然估計（maximum likelihood estimation，MLE）方法進行求解。計算出檢測時刻ti上各分布模型的差異程度后，選取差異程度最小所對應的分布作為時刻ti的退化量模型，從而求解出各檢測時刻ti上退化量失效率值。

產品在工作一段時間后出現性能退化現象，通常是由多種物理或化學失效模式共同影響的結果，而且退化影響機理會隨著時間的推移而發生變化。因此，不能僅用一種特定的壽命分布（如正態分布）類型來一概表示產品整個退化失效過程，而應該根據不同時刻收集到的性能退化數據進行分布擬合檢驗，選擇分布差異度最小的分布類型來描述該時刻的產品退化失效趨勢，這樣更符合工程實踐和經驗認識。

2.4 比例失效率退化模型

現以檢測時刻為協變量，將產品各檢測時刻上性能退化數據引入比例危險模型，并推廣為比例危險退化模型（proportional hazard degradation model），從而來描述產品壽命與性能退化失效率之間的關系。

設各檢測時刻ti（i＝1，2，…，n）構成給定的單因素協變量t，在協變量t下產品性能退化量的可靠度函數為R（y／t），密度函數為f（y／t），則產品退化量失效率函數可表示為

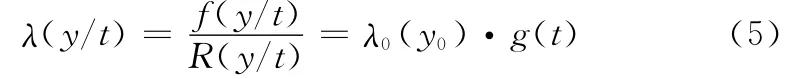
式中，λ0（y0）為選定的基準時刻t0上退化失效率函數；g（t）為與協變量t有關的函數。

由于不同檢測時刻上收集到的性能退化數據類似于突發失效下的加速壽命數據，可將時間t類比為一種加速因子，從而建立比例失效率退化模型，即

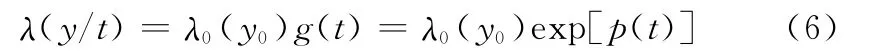
式中，p（t）為類加速模型。

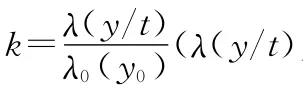
令為時刻t上退化失效率函數），稱k為時刻t相對于基準時刻t0的退化失效比例系數，則p（t）可用時間與退化失效比例系數之間的函數關系表示如下：

經退化數據結構分析，［t，ln k］之間采用線性回歸模型較為適用，則式（7）轉變為

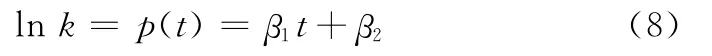
3 壽命可靠度

3.1 壽命可靠度函數

由式（1）和式（6）可得基于比例失效率退化模型的產品退化量可靠度函數為

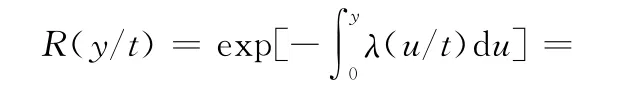
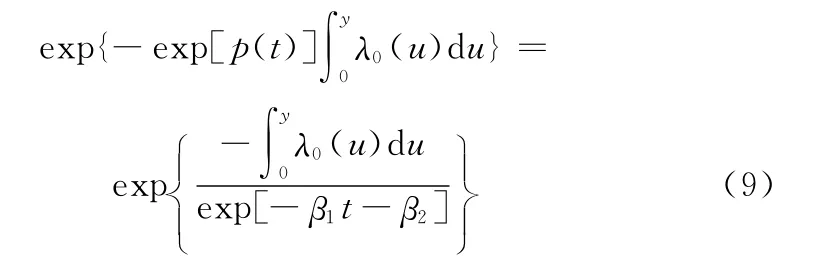
說明：上式成立的必要條件是基準失效率函數λ0（u）是可積函數。若λ0（u）不可積，則可以依據所計算出各時刻上的退化量失效率離散值，繪制出產品退化失效率曲線，采用可積的回歸模型（如二項式）進行擬合，得到的函數表達式~λ0（u）可近似作為基準失效率函數［15］。

令y為退化失效閾值yc，由式（3）可得產品退化失效的壽命可靠度函數為

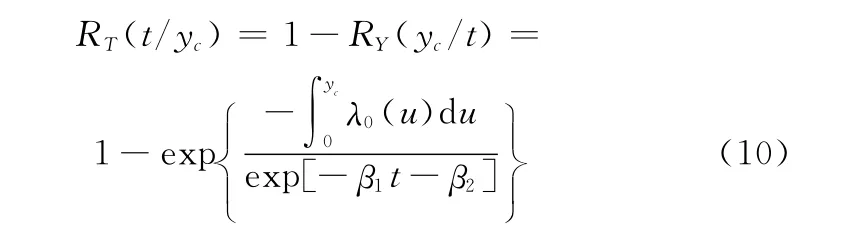
3.2 參數估計

（1）選定基準時刻t0

根據各檢測時刻所確定的分布模型情況，選定同一類分布較為集中的時刻為基準時刻t0，并以該時刻上的退化量失效率函數作為基準失效率函數λ0（y0）。

（2）類加速模型參數β1，β2

確定各檢測時刻產品退化量分布模型后，計算出各檢測時刻ti上第j個產品的退化失效率λ（yij／ti），則檢測時刻ti相對于基準時刻t0的退化失效比例系數ki估計為

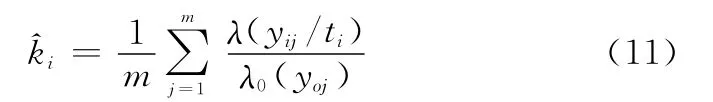
由式（8）知，參數β1，β2估計可由［ti，ln＾ki］擬合求出。

4 實例分析

引用文獻［5］的某型激光器退化數據進行分析處理，每隔500h抽取退化數據構成樣本數據（見表1），并與文獻［6，8，15］采用的方法所得到的結果進行比較分析。當產品電流增加值達到額定值的10%時就認為產品失效，繪制各樣本的性能退化軌跡（見圖1），具體評估過程如下。

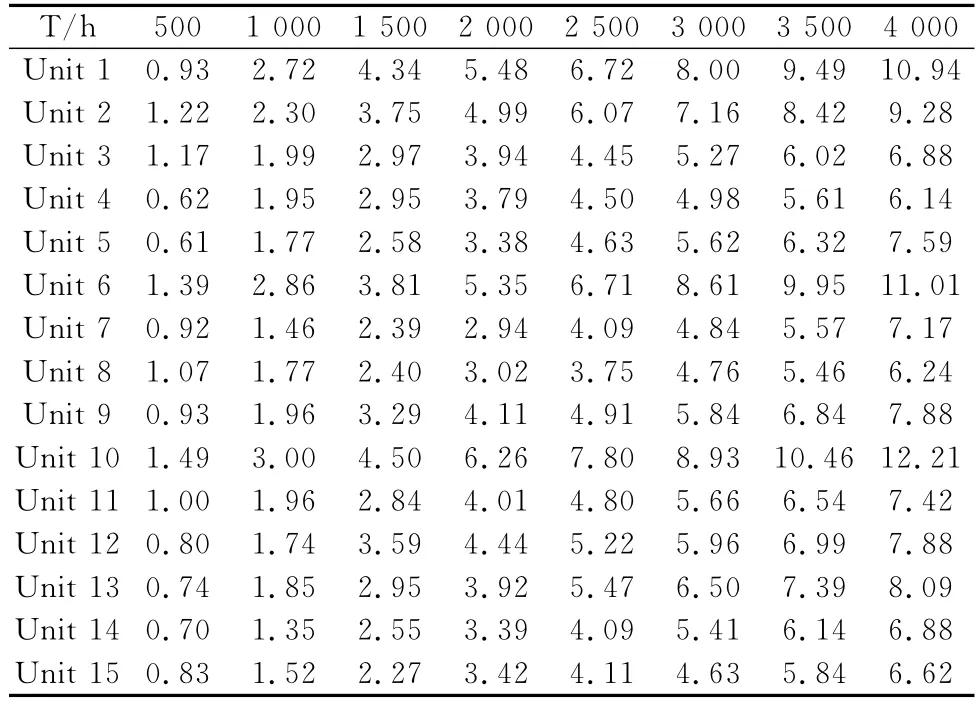
表1 某型激光器性能退化樣本數據

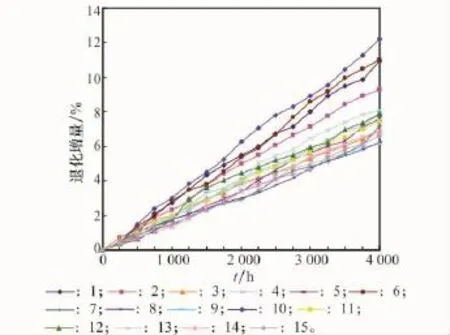
圖1 產品性能退化軌跡

（1）確定各檢測時刻的退化量分布模型。假設可能的退化分布簇包括：正態分布、對數正態分布、威布爾分布和伽瑪分布。根據各檢測時刻上的產品退化數據，運用Matlab軟件計算各時刻可能分布模型之間的差異度（見表2），則500h時刻的退化量分布模型是伽瑪分布，1 000h、1 500h、2 000h、2 500h、3 000h時刻的退化量分布模型是威布爾分布，3 500h、4 000h時刻的退化量分布模型是對數正態分布。

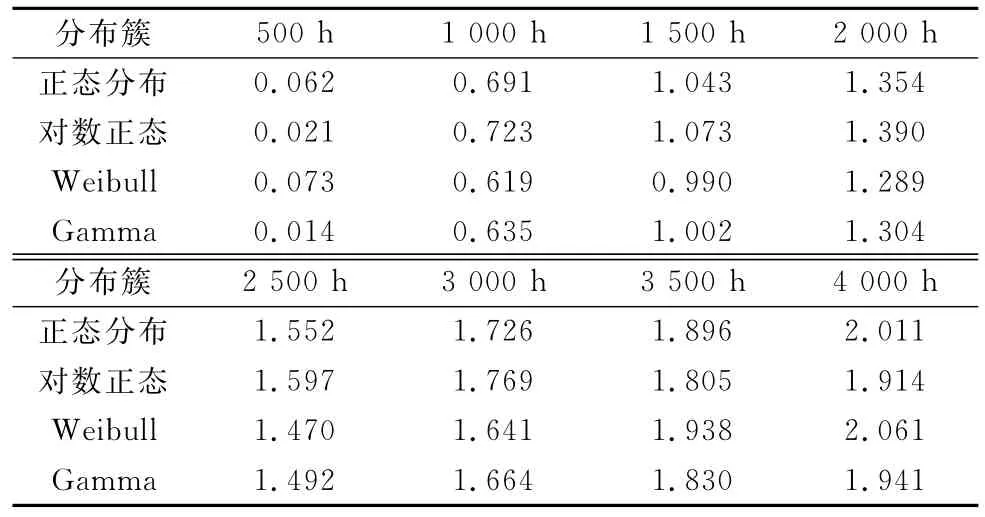
表2 分布簇之間的差異度

（2）根據各檢測時刻上所確定的分布模型，計算出各時刻的樣本退化量失效率的離散值，繪制退化失效率的軌跡曲線（見圖2）。

由圖2可見，各檢測時刻上退化失效率曲線在退化數值上呈現出一定比例關系，且隨著時刻ti的增大，退化失效率曲線的比例（類似斜率）逐漸減小，適用于比例失效率退化模型。

（3）確定基準失效率及比例系數

由于1 000h、1 500h、2 000h、2 500h、3 000h時刻上的退化量分布模型都是威布爾分布，同一類分布較為集中，可選取t0＝3 000h為基準時刻，將其退化失效率函數作為基準失效率函數λ0（y）。由MLE方法可得其參數點估計且此時該函數可積，則λ0（y）可表示為

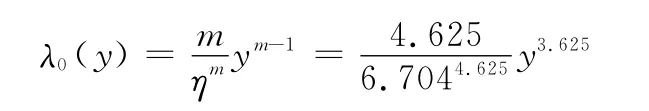
由式（11）計算出，ti＝500h、1 000h、1 500h、2 000h、2 500h、3 500h、4 000h相對于基準時刻t0＝3 000h的比例系數分別為＾ki＝5.162，2.825，2.053，1.465，1.181，0.809 2，0.726 6。

（4）確定產品壽命可靠度

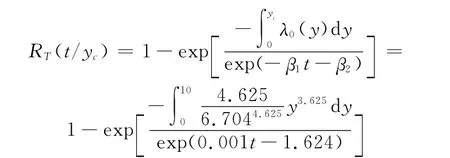
（5）不同方法對比分析

根據產品的壽命可靠度函數以及文獻［6，8，15］中的方法所得到的壽命可靠性函數，繪制各方法下的產品壽命可靠度曲線（見圖3）。

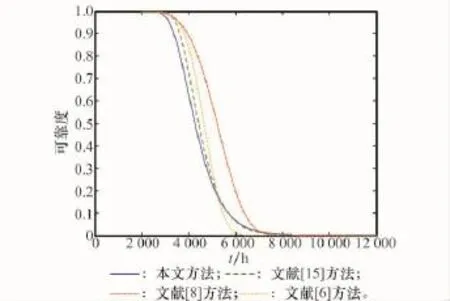
圖3 不同方法下產品可靠度曲線

由圖3可見，本文方法得出的產品可靠度曲線在與文獻［6，15］所得的可靠度曲線在（5 180h、0.187 7）處交匯。在交匯點之前，本文方法所得的可靠度曲線略低于其他曲線，評估結果略顯保守；在交匯點之后，本文方法所得的可靠度曲線與文獻［15］所得的可靠度曲線基本吻合，都處于文獻［6，8］所得曲線之間。對于高可靠性產品而言，工程技術更關注產品在高可靠度下的可靠壽命，本文方法得出略顯保守的可靠度評估結果符合工程上對產品壽命的要求。因此，在處理非加速條件下的性能退化數據時，本文方法具有所需樣本數據少，模型假設條件少，評估結果客觀真實等優點，具有良好的適應能力和工程應用價值。

5 結 論

從退化失效角度進行退化數據可靠性建模，可以有效解決高可靠長壽命產品可靠性評估問題。比例風險模型是一種基于基準失效率函數的建模方法，通過非參數統計法獲取產品的可靠度。本文引入比例風險模型，建立了不同于傳統基于退化軌跡和基于退化量分布的退化數據可靠性評估模型，即不假定產品壽命分布類型，將時間視為類加速因子并作為協變量，建立比例失效率退化模型，通過考慮分布簇之間的差異度來確定退化量分布類型，計算出各時刻退化量失效率，求出基準退化量失效函數，實現了對退化失效數據的可靠性評估。結合實例表明，本方法對求解產品退化量失效率呈比例變化的退化失效問題是科學有效的，具有較好的應用價值。

［1］Zhao J Y，Liu F，Xi W J.Reliability model and evaluation method of products in competing failure modes［J］.Acta Armamentarii，2011，32（8）：1136－1139.（趙建印，劉芳，奚文駿.退化失效與突發失效共存下產品可靠性模型與評估方法研究［J］.兵工學報，2011，32（8）：1136－1139.）

［2］Lu J C，Meeker W Q.Using degradation measures to estimate a time-to-failure distribution［J］.Technometrics，1993，35（2）：161－174.

［3］Crk V.Reliability assessment from degradation data［C］∥Proc.of the Annual Reliability and Maintainability Symposium，2000：155－161.

［4］Chen L，Hu C H.Review of reliability analysis methods based on degradation modeling［J］.Control and Decision，2009，24（9）：1281－1287.（陳亮，胡昌華.基于退化建模的可靠性分析研究現狀［J］.控制與決策，2009，24（9）：1281－1287.）

［5］Deng A M，Chen X，Zhang C H，et al.Reliability assessment based on performance degradation data［J］.Journal of Astronautics，2006，27（3）：546－552.（鄧愛民，陳循，張春華，等.基于性能退化數據的可靠性評估［J］.宇航學報，2006，27（3）：546－552.）

［6］Zhong Q H，Zhang Z H，Wu H S.Research on methods about reliability assessment based on degradation data［J］.Systems Engineering and Electronics，2009，31（9）：2280－2284.（鐘強暉，張志華，吳和聲.基于退化數據的可靠性評估方法探討［J］.系統工程與電子技術，2009，31（9）：2280－2284.）

［7］Chen Z H，Zheng S R.Life distribution based degradation analysis［J］.IEEE Trans.on Reliability，2005，54（1）：3－10.

［8］Zhong Q H，Zhang Z H，Wang L.Approach about degradation data analysis considering model selection［J］.Systems Engineering，2009，27（11）：111－114.（鐘強暉，張志華，王磊.考慮模型選擇的退化數據分析方法［J］.系統工程，2009，27（11）：111－114.）

［9］Cox D R.Regression models and life-tables［J］.Journal of Royal Statistical Society，1972，34（2）：187－220.

［10］Eghbali G.Reliability estimate using accelerated degradation data［D］.USA：The State University of New Jersey，2000.

［11］Huang W，Duane L.An alternative degradation reliability modeling approach using maximum likelihood estimation［J］.IEEE Trans.on Reliability，2005，54（2）：310－317.

［12］Zhao W B，Elsayed E A.An accelerated life testing model involving performance degradation［C］∥Proc.of the Annual Reliability and Maintainability Symposium，2004：324－329.

［13］Mohammed A H，Ebrahem J J H.Non-parametric analysis of a proportional wearout model for accelerated degradation data［J］.Applied Mathematics and Computation，2006，174（1）：365－373.

［14］Zhong Q H，Zhang Z H，Liang S J.Approach for degradation data analysis based on proportional failure rate model［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38（1）：43－47.（鐘強暉，張志華，梁勝杰.基于比例失效率模型的退化數據分析方法［J］.北京航空航天大學學報，2012，38（1）：43－47.）

［15］Su C，Zhang Y，Zhang H.Product reliability assessment based on proportional hazard degradation model［J］.Journal of Southeast University（English Edition），2010，26（3）：480－483.

Method on reliability assessment based on proportional failure rate degradation model

CAI Zhong－yi，CHEN Yun-xiang，ZHANG Zheng-min，XIANG Hua-chun
（Equipment Management ＆Safety Engineering College，Air Force Engineering University，Xi’an 710051，China）

Aiming at the problem of long-lifetime reliability assessment in the assumption of unknown life distribution，a new method on reliability assessment for degradation data is proposed，which is different from the traditional method based on the degradation path and degradation measure distribution.Time is treated as a similar-accelerated factor and used as a covariate.The relationship between the lifetime and the degradation failure rate of the product is described by the proportional hazard model and the proportional rate model is built.The degradation distribution is determined through the divergence of the distribution set，and the degradation basic failure rate function and its proportional rate coefficient are obtained.The linear regression model is used to evaluate the parameters of the similar-accelerated model，and the degradation failure rate function in certain detection time points is determined.The lifetime reliability function of the product under the predetermined degradation failure threshold is obtained.An example is provided to demonstrate the validity of the proposed method.

degradation data；reliability assessment；proportional hazard model；distribution divergence；basic failure rate

TB 114.3

A

10.3969／j.issn.1001-506X.2015.08.34

蔡忠義（1988－），男，博士研究生，主要研究方向為裝備可靠性與系統工程。

E-mail：afeuczy＠163.com

陳云翔（1962－），男，教授，博士，主要研究方向為裝備發展論證、裝備維修保障。

E-mail：cyx87793＠163.com

張諍敏（1964－），女，教授，碩士，主要研究方向為裝備系統工程。

E-mail：646297491＠qq.com

項華春（1980－），男，副教授，博士，主要研究方向為裝備可靠性與系統工程。

E-mail：xhc09260926＠163.com

1001－506X201508－1943－05

網址：www.sys－ele.com

2014－11－03；

2014－12－19；網絡優先出版日期：2015－03－17。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150317.1127.009.html

總裝“十二五”國防預先研究項目資助課題