運用“三法”巧解數學問題

陸曉蘭

解決問題作為綜合與實踐的重要組成部分，在小學數學知識結構中占舉足輕重的地位。它是以一類問題為載體、以學生自主參與為主的學習活動。在教師的適當指導下，學生能夠在面對問題時，有效整合自己已有的知識、技能和經驗，并通過合理的運用和轉化，達到未知目標的過程，在這一過程中，學生的情感、態度、價值觀均得到了發展，數學的意識和創造性思維也有所提高。本文就小學階段的幾道典型數學問題進行探討，以此展示如何創新性巧解問題，希望對一線的教師有所幫助。

一、運用“假設法”巧答定義問題

假設法是數學解題的重要方法之一。通過假設可以使復雜的問題簡單化，使所求的問題明朗化，幫助學生很快地找到解決問題的突破口，從而使問題化難為易。

在小學數學教學中，筆者發現學生在學習除法時，容易產生這樣一個疑問：“為什么在數學運算的過程中，0不能作除數？如果現在回過頭來看乘法和除法，它們之間存在著一個互為逆運算的關系。即若有a×b=c，則有c÷a=b（a≠0）。現在假設a=0時也成立，此時有：

當a×1=0，則0÷a=1；

當a×2=0，則0÷a=2；

當a×3=0，則0÷a=3；

當a×4=0，則0÷a=4；

當a×n=0，則0÷a=n（n為非零自然數）。

顯然，當a×n=0無限進行下去時，此時0÷a的商不唯一，這就與商的唯一性相矛盾。這就解釋了為什么0不能作除數的原因。像數學中的很多重要的定理、定義，都可以采用“假設法”的方式，向學生解釋其邏輯性和嚴密性，從而讓學生知其然，也知其所以然。

二、運用“作圖法”巧解土地問題

作圖法是把應用題的數量關系表示出來，使題意形象具體，一目了然，以便較快地找到解決問題的途徑，它對解答條件隱蔽、復雜疑難的應用題，能起到化難為易的作用。

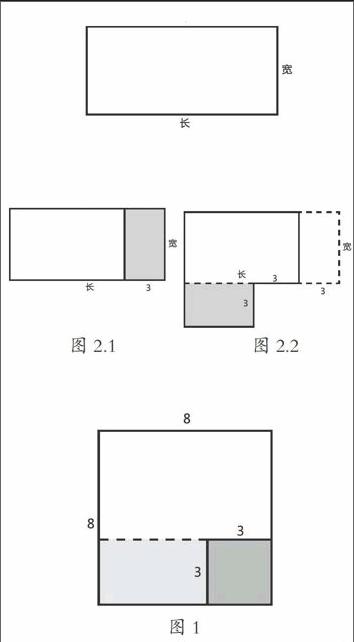
筆者在數學教學過程中，遇到了這樣一個問題：有一塊長方形菜地，面積為55平方米。長比寬多6米。問長和寬分別有多少米？顯然，對于此類問題，以小學階段的數學知識，是無法解決這一問題。但在古巴比倫的數學中，就涉及了通過作圖來解決這一二元一次方程問題：

第一步：按照要求畫一個長比寬多6米的長方形（如圖1）；

第四步：重組的正方形面積為55+9=64（平方米），故邊長為8米。因此原來長方形的長為8+3=11（米），寬為8-3=5（米）。

通過作圖，這道題目立馬顯得簡單明了，可見作圖法的作用非常強大。由于小學生正處在直觀形象思維階段，將抽象的數學與直觀的圖形巧妙的結合在一起，能夠讓學生更直觀地發現數量關系，這不僅有利于提高學生的學習興趣，激發學生的思維，同時也開闊了學生的解題的思路，提高解題能力。

三、運用“轉化法”巧解生活問題

轉化法指將未解決的或待解決的問題，通過某種途徑轉化為已解決的或易解決的問題，最終使原問題獲得解決的一種方法原則。筆者在教學蘇教版四年級數學上冊《整數四則混合運算》中的“求兩積之和（差）的實際問題”時，設計了這樣一道題：一個旅游團去公園游玩，成人18人，兒童14人。成人票每張25元，兒童票半價，旅游團購買門票應付多少元？

本題通常的做法是先明確數量關系：成人總票價+兒童總票價=應付的錢，根據條件分別表示出成人總票價和兒童總票價兩個量即可解答。成人票總價是25×18，但兒童票的單價是以成人票單價的一半出現，那么兒童票單價為25÷2=？顯然四年級學生以現有知識是無法解決這個問題，思考頓時陷入了瓶頸。經過幾分鐘的思考后，學生會發現有以下幾種解決方案：

①把25元化成了250角后再求兒童票單價；

②兒童票是成人票價的一半，故可以把14個兒童轉化看作7個成人。即可以列算式25×（18+14÷2）；

③先把14個兒童看成14個成人，求出票價后再除以2就得到14個兒童的票價了，算式是18×25+14×25÷2。

通過運用轉化的方法，將未知的轉化為已知，并以一題多解的形式，既可以讓學生在多種解法中比較，從中選出最快最好的解法，同時也給了學生今后解題時探尋最優化解題方法做了深透。經常組織學生進行這樣的訓練，有利于學生自主建構知識之間的聯系，發展學生在解題時的思維敏捷性創造，培養學生的發散性思維能力，鼓勵學生積極主動地參與到數學活動中去，讓他們覺得數學簡單有趣。

以上的三類解決問題的方法，是筆者在數學教學學習過程中所接觸到的。在解題的過程中，由于學生已儲備了相關的知識經驗，形成了一定程度上的思維慣性。當學生在調用原有經驗來解決新問題時，發現在計算上出現問題，使得原有的知識系統受到干擾，一時間如果他們無法獨立對新、舊知識進行溝通和整合，就會出現對問題質疑的現象。此時，教師必須就要學會對學生在課堂中發出的聲音“把脈”，做到適時地介入與科學地處置，從而開啟學生思維的盲點，“焊接”學生思維的斷層，有效克服學生的思維慣性，從而提升學生創新能力和解決問題的能力[1]。合理恰當地運用上述方法和技巧來解決數學問題，可以收到良好的效果。

【作者單位： 昆山市陸家中心小學校 江蘇】