有效教學理論下的數學雙基教學和數學變式教學*

南通師范高等專科學校 錢美蘭

1 雙基教學

1.1 “數學雙基”的界定

何為數學雙基？張奠宙先生指出，“數學雙基”指“數學基本知識”和“數學基本技能”，這不因任何歷史階段的改變而改變。田中、徐龍炳、張奠宙認為數學基礎知識主要包括以下三個方面：知識、方法、思想。他們認為數學的基本技能蘊含“在實踐的基礎上”和“有一定的規則或操作程序”這兩點，總結了運算、推理、繪圖三種基本技能的延伸。鄭毓信從認知角度對“數學雙基”提出了“結點說”。他認為，將數學的法則、公式、命題、概念等看成知識網絡或概念網絡中的結點，根據結點連接的廣泛程度看出其重要性，進而產生“數學基礎知識”；根據問題解決時所需要的程序應用的深度和廣度，可以決定“數學基本技能”。

1.2 “數學雙基教學”的主要特征

一直以來，數學教學堅持打好基礎，遵循基礎知識教學和基本技能應用的“雙基”原理具體表述如下：

從課堂組織形式上看，我國數學基本上沿襲“復習—新知識探究—分析實例—實踐整合—課堂教學小結—作業”的教學方法。這種課堂教學組織形式較為固定，包括六個傳統教學環節“復習舊知導入新課—帶著新問題探究新知—分析與講解例題—作業鞏固小結—整節課小結—布置課后作業”，各個環節要求和目的都十分明朗化。

從課堂教學的成效上看，注重效率，避免彎路，直接體現了教學內容的側重點。受應試教育的影響，“雙基教學”被理解為“考試的雙基”，為了幫助學生盡快掌握知識點，提高學習效率，課堂教學中教師主要在新知呈現及例題梳理這些環節上盡快展現數學內容，避免學生走彎路。如特別在介紹定義、原理及相關公式時，為了讓學生能盡快記住定義、定理及公式，許多教師略講定義、原理及公式產生的背景與過程，直接將之呈現出來，讓學生有目的地去記憶。這種方法確實能節約不少時間，將更多的時間投入到解題訓練中去，雖實現了“精講多練”，但最終必導致學生知識的遺忘率也高。

從培養能力的角度上看，注重學生的邏輯思維能力。主要包括概念的辨析、無重復無遺漏的分類、主要公式的記憶、知識點的邏輯關系和掌握數學解題的流程，還有數學解題套路的熟悉，尤其是形式化的邏輯演繹證明。如分類不重復不遺漏, 解題過程前后要等價，分母不能等于零，絕對值不為負值，被開方數不能為負值等等，反復強調、訓練。

從思維訓練上看，注重學生數學思想與方法的培養，反復進行大量解題訓練。例如，分類討論，數形結合，特殊到一般，函數與方程，分析、歸納、綜合、類比、演繹、化歸的概括和應用。

2 變式教學

《論語·述而》記載：“舉一隅，不以三隅反，則不復也”，體現了孔子時期 “變式教學”觀念就已經產生。“數學變式教學”是我國最重要的教學模式之一，也是廣大教師在課堂實踐中使用的最重要的教學方式之一。通過變式教學，學生可憑自己已有的認知結構或感性經驗及相關能力去領會事物的本質并提升自己對問題的新認識。這對訓練學生的思維，使之達到廣闊、深刻與靈活，有著非常重要的意義。

2.1 “數學變式教學”的界定

所謂“數學變式教學”，是在數學教學過程中不改變本質特點，但不斷地改變數學概念的條件，建立各種應用環境，使學生在任何變化過程中都能認清本質的一種教學方法。

2.2 “數學變式教學”的主要特征

數學變式教學主要具備如下兩個特征：

第一，對概念的多角度理解。概念性變式教學通過多概念間及概念的本質特征與非本質特征的區別與聯系來把握概念的本質屬性，從而實現對概念多角度的理解。這樣，有利于學生真正理解概念的本質，從而建立新概念與原有概念的區別與聯系。如代數中復數分類的理解及立體幾何中柱體、錐體與臺體合理的分類等。

第二，展現數學活動經驗的多層次性。這種多層次性主要體現在：幫助學生循序漸進地學習概念的邏輯過程，歷史過程或者心理過程；使學生的間接解決活動具有多個臺階或者多種途徑來解決問題；構成一個多層次的經驗系統促進學生形成認知結構。這種有層次推進的變式使學生原有分散的、零碎的活動經驗成為一個有機整體，這樣可以幫助學生優化知識結構并做到融會貫通。

3 有效教學理論下的雙基教學和變式教學

3.1 有效教學理論下兩種教學的有效性

3.1.1 數學雙基教學模式的有效性

由于我國數學教育狠抓基礎，落實雙基，因此我國學生的數學基礎較扎實，并且他們有的在各屆國際數學比賽中大獲全勝，從這些方面不難看出我國堅持數學雙基教學的正確性和有效性。現從如下三方面評述其有效性：

第一，教學過程中十分重視知識掌握與技能訓練的有效性。無論是概念與原理的提出，課堂練習與應用，教學中總是不斷圍繞以知識為中心，以練習為中心開展教學的。課堂上師生共同歸納出概念與原理，再對概念與原理的理解給出相應的變式理解，目的是進一步理解好基礎知識的本質內涵。接下來是基本技能的訓練。無論是一題多解還是一題多變還是一法多用，目的就是為了進一步將知識點達到理解并靈活運用，基本技能的訓練達到自動化、爐火純青的地步。總之，雙基教學一個最突出的優勢就是打好知識基礎，抓好技能訓練。

第二，教學過程中十分重視發揮教師的主導作用。教師理所當然地成為課堂上的引導者、組織者與管理者，通過嚴謹周密的布置，逐步引導整個課堂教學活動朝著既定的目標發展，課堂時間得到合理而有效的利用。

第三，追求課堂教學效率的教學是非常重要的。正如前面所提到的，為了避免學生走不必要的彎路，在教學過程中關于概念的提出與技能的訓練基本都是由教師掌控。教師先創設合理的情境將新知盡快呈現，經過講解分析，引導學生快速理解新知，接下來再通過一定預設的例題讓學生對新知加以鞏固吸收，再通過一系列的變題，使學生領悟數學的思想和方法，全面吃透新知識的本質。總之，一節課完全在教師的有效掌控之下，按照教師的意愿開展相關活動，極大地提高了教學效率。

3.1.2 數學變式教學模式的有效性

變式教學可以使學生有意識、有目的地辨析同類事物的非本質特征從而增強對事物的本質屬性的認識。數學變式教學能促進學生學習的主觀能動性，可以幫助他們利用所學知識融會貫通，領略數學的魅力，體味數學學習的樂趣。鮑建生等在其系列論文“變式教學研究”中作了系統研究，他們認為：第一，變式教學有利于數學概念的掌握。從具體直觀的變式多角度導入概念與原理，幫助學生掌握概念的內涵及外延。第二，變式教學有利于數學經驗的增長。能促進數學活動的有層次推進，用于概念的形成過程和用于問題解決的教學以及用于取得特定的活動經驗，有利于學生數學活動經驗的增長。

3.2 有效教學理論下兩種教學的局限性

3.2.1 數學雙基教學的局限性

數學雙基教學也有其局限性。數學雙基教學雖然在我國的教育史上具有不可磨滅的作用，但一直以來由于我們過分注重雙基教學，忽視了數學在人的發展過程中其他方面的價值，致使雙基教學出現了異化。概括起來主要表現為：

3.2.1.1 注重教師的主導地位，忽視學生的主體地位

眾所周知，學生是課堂學習的主體。但是在傳統課堂上卻是由教師主導，甚至強行灌輸式教學模式。學生在這種束縛之下，主體地位被抹煞，情感與價值觀得不到體現，需求得不到滿足，想法得不到溝通與理解，上課枯燥無味，課堂沉悶，失去活力。

3.2.1.2 注重解題訓練，忽視數學基本思想方法的培養

教師對題目的講解和示范按照既定套路進行，重點往往是放在如何做和具體的解題方法及技巧上，而對于為何要這樣做，以及如何想到解題思路等問題卻很少涉及。這樣使學生喪失了在熟練掌握解題技能的基礎上進一步對解題思想方法與策略進行升華，使解題能力得到提高的機會。傳統教學中經常碰到一道題目講解多遍，一段時間后拿出來哪怕是稍作變化后，仍不知如何解題，就像楊振寧教授所說的，我國學生知識太多，活的思想太少。

3.2.1.3 注重雙基的夯實，忽視對學生數學的應用意識與創新能力的培養

我們不能局限于僅僅打好基礎。打好基礎的目的是為了進一步創造更輝煌的業績。一個科學的數學教育理論，必須同時研究“基礎”和“創造”兩方面。缺乏基礎的創新是天馬行空，缺乏創新的基礎是機械重復。故培養學生的發展要注重“基礎”與“創造”相結合。

3.2.1.4 注重數學的考試作用而忽視數學文化對人的發展的重要作用

在課堂上，注重教知識、練技能而忽視知識產生的背景及在生活方面的應用的教學屢見不鮮。如“掐頭去尾燒中段”式課堂教學，學生思考、探究、實踐的機會與時間大大缺乏，即使有的討論與合作也是流于形式。在這樣的“雙基教學”活動中，毫無學生的主體性可言，雙基教學成為了低層次的傳授知識或訓練技能的活動，這些都使得雙基教學的育人價值大打折扣，忽視了數學文化在人類發展中的重要作用。

3.2.2 數學變式教學的局限性

許多教師片面地理解變式教學。其實，概念或原理的變式教學過分強調知識本身的結構性、系統性、嚴密性而忽視與其他知識間多角度的相互聯系。解題訓練則過分強調解題速度的自然化、迅速化而忽視解題思想與方法及解題策略的研究。還有人簡單地認為變式訓練就是變式教學，效果好，于是大搞題海戰術。教學中將題目分組，分類，分專題，機械化、套路式地進行訓練，但又從不注重反思總結提升，結果學生前做后忘，知識遷移能力并沒有得到實質性提高，教學毫無效果可言。

4 基于兩種教學下的案例分析

日常教學過程中，教師對公式內容的證明過程常分析不到位，或直接給出公式或稍微帶領學生瀏覽一下書本上的證明過程就完事。這種重知識而輕過程的學習方式極大地阻礙了學生思維的發展。因為公式的形成過程中往往富含許多先進的數學思想與方法，教師對公式的證明過程，對培養學生學習的嚴謹性、科學性與邏輯性，培養學生優秀的思維品質與創新思想舉足輕重。以下以同角三角函數的基本關系為例來說明如何進行公式教學。

4.1 教學內容分析

本節課主要學習內容為理解與掌握同角三角函數的兩個基本關系式，進而是應用公式進行化簡、求值與證明，主要是讓學生體會到同角三角函數值之間的相互聯系。本節課可從兩個角度對關系式進行證明。一是從代數角度——借助三角函數定義來猜想并證明關系式，讓學生認識到事物之間的普遍聯系性；另一方面從幾何形式——三角函數線角度給予數形結合的證明，讓學生更加直觀地認識同角三角函數關系。

4.2 教學重點和難點

（1）教學重點：①同角三角函數基本關系式的推導證明；②應用同角三角函數基本關系式進行化簡、求值和證明。

（2）教學難點：同角三角函數基本關系式的靈活應用及學生思維品質的養成。

4.3 學情分析

①提到函數，在學生頭腦中就是一個“偏、繁、難”的印象，但是這節內容是關于公式的介紹，學生明顯會感覺興趣有所提高，學習的欲望加強。

②借助三角函數的定義、三角函數線等內容作鋪墊，學生能在教師的引導下完成公式的探討。

③高職數學更注重思維訓練，當前學生已具備一定的邏輯思維能力與解題能力，所以這節課重在培養學生的自主學習與應變能力。

4.4 教學過程設計

（1）問題引入

問題1：任意角α的三角函數的定義？

問題2：三角函數值的符號問題？

問題3：通過三角函數的定義，猜想任意角α的三角函數值間所滿足的等量關系，并給出證明？

問題4：如何用三角函數線證明基本關系式？

問題5：你能提出哪些與關系式應用相關的問題？

問題 6：如果僅已知tanα=2，能否求出sinα,cosα的值？

（2）新知探討

通過課前預學，自主學習與小組合作交流，加上教師適當引導點撥，證明同角三角函數基本關系式的兩種方法。

證法一：利用三角函數的定義，通過觀察分析定義中字母間的關系，構造等量關系得出結論。

證明：

證法二：利用單位圓與三角函數線的知識，通過構造直角三角形，利用數形結合思想，直觀形象地得出關系式。（3）例題講解

例1公式辨析：

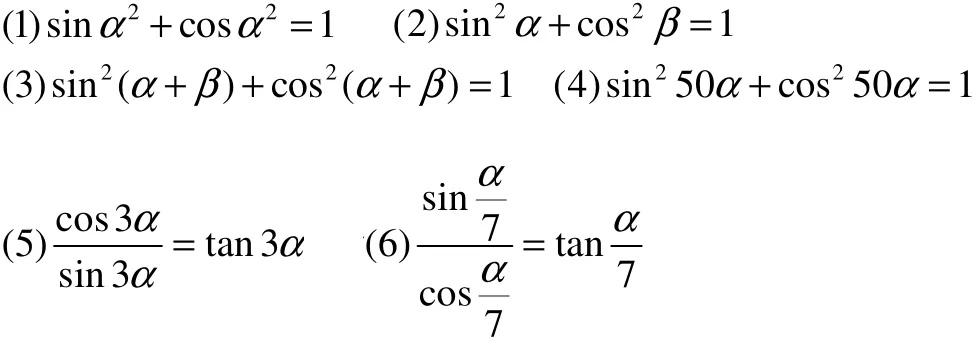
答案:成立的有(3)、(4)、(6)

思考：猜想同角三角函數的基本關系有哪些具體運用？

變式2 已知tanα=2，且α是第一象限角，求sinα,cosα的值.

變式3 已知tanα=2，求sinα,cosα的值.

（4）課堂小結

①已知任意角的某一三角函數值，根據基本關系式能求其余兩個，即“知一求其余”，打好基礎。

②應用基本關系式來計算、化簡及證明簡單的三角函數式，培養遷移與應變能力。

（5）布置作業

習題 4.2 3，4，5，9，10，13，15

（6）課例反思

對該課例進行反思分析，本節課以“巧設問題—合作探究—變式訓練”為主線展開教學。

一切從學生的發展出發是本節課最大的亮點所在。首先從兩個方向證明同角三角函數基本關系式，培養學生多角度看待并思考問題的能力。而接下來的例題研究，如例1的意圖主要是通過對關系式的辨析，讓學生充分理解基本關系式的本質特征。例2是一道基礎題，主要是公式的直接應用，將關系式與三角函數值在各象限的符號結合起來求解問題。與例2相比，變式1中角所在的象限未知，這就要根據題意首先確定出角可能是第幾象限角，這樣自然而然要進行分類討論。故這道變式十分經典，能使學生的思維層次得到明顯上升，有一種云開霧散的感覺。接著的變式2、3，改變了題設和結論，此時卻可采用解方程組的方法求解問題，雖難度逐步加大，但能較好地加強學生對公式的靈活掌握。而最后的變題 4，角度更多更廣，本題至少有三種方法求解。該題雖然思維更活躍，但大部分同學都能至少能用一種方法做出來，而對于其中的“弦化切”思想更要關注。這四條變題的選擇很有思維層次感，它們往往會使學生覺得這道題肯定會做，但解起來又會碰到新的問題而必須駐足徘徊思考。因此它們最大限度地使學生靈活運用公式功不可沒。由于本例題及變題以問題串的形式展開教學，前后問題層層遞進引人入勝，充分體現了問題是獲得一切知識的源泉，問題又是解決一切問題的動力。當然，問題更為促進生生互動及師生對話提供了鮮明的背景。

通過深入分析這節課，筆者認為可以在平時的數學教學活動中適度運用變式教學，通過對概念與原理的一題多變，對練習的多角度求解與變換等，引導學生辨析事物的非本質特征，逐步加強學生對事物的本質認識。本節課就是如此，通過例2進行適當合理的變式，設計過程實施得非常順利，學生自主合作，積極踴躍，努力克服前進路上的困難，教學目標基本達成。這也符合了新課程的改革趨勢，以學定教，以學生為本，極大地調動學生的學習激情。相關例題的教學使學生的思維也得到了極大地鍛煉，學生收獲了一定探索性學習的方法與策略，并最終享受到了成功的喜悅。

[1] 張奠宙.中國數學雙基教學理論框架[J].數學教育學報，2006（3）:1.

[2] 鄭毓信,謝明初.“雙基”與“雙基教學”:認知的觀點[J].中學數學教學參考,2004(6):2.

[3] 紀宏偉. 談中學數學教學中的“五個注重”[J].華夏教師，2014（12）：25.

[4] 張奠宙.話說“數學雙基”[J].湖南教育,2007 (l):5.

[5] 張奠宙，李士锜.數學“雙基教學”研討的學術綜述[J].中學數學教學參考,2003,1～2.

[6] 邵光華,顧泠沅.中國雙基教學的理論研究[J].教育理論與實踐, 2006,26(2):48-52.

[7] 紀宏偉. 例習題教學中的變式教學——以涂色問題為例[J].數學教學研究，2014（5）：61-64.

[8] 紀宏偉. 對一題多解教學的思考[J].中學數學月刊，2014（6）：32-34.

[9] 崔允漷.有效教學:理念與策略(上)[J].人民教育,2001(6):46-48.

[10] 鮑建生，黃榮金，易凌峰，顧泠沅.變式教學研究[J].數學教學，2003（2）：6-10.