滬深300指數期權仿真交易市場的有效性研究

■孫桂平

一、引言

伴隨著全球衍生品的發展，期權類產品也逐步發展，股指期權作為一種金融衍生品市場中成長迅速的投資避險工具，具有對整個衍生品市場的促進和規范作用。目前，美國、德國、法國、韓國、印度、中國香港和中國臺灣等主要國家和地區都推出了自己的股指期權產品。

目前我國也在計劃推出自己的股指期權產品，滬深300指數期權仿真交易于2013年11月在中國金融期權交易所推出，已經運行了一年多時間。股指期權仿真交易推出后，其市場的運行效率問題是學術界、企業界和監管者都共同關心的問題，仿真市場能否有效運行直接關系到期權交易正式推出的時間，以及未來正式期權交易的合約設計和交易規則的制定等一系列問題。

股指期權市場在國外出現后，其市場效率問題一直是研究的熱點。市場效率研究開始采用的方法是利用期權定價模型來檢驗期權市場價格的有效性，該方法的優點是可以直接觀察到期權市場價格和理論價格之間的偏差，但是也存在著很大的缺陷，主要原因在于定價模型本身不準確，模型的許多假設在實際市場中往往不成立。

其后市場效率的研究主要基于無風險套利的角度進行，該方法假定在成熟有效的期權市場上不存在無風險套利的機會。該方法不依賴于具體的期權定價模型，不需要計算市場的波動率，所需的假設很少，國外學者通常采用該方法對國外期權市場的效率進行分析。

再后來，有專家學者運用期權平價關系式，采用事前分析和事后分析的方法，并利用牛市價差條件、蝶式價差條件和盒式價差條件對股指期權的市場內效率問題進行研究。

與國外眾多的研究成果相比，目前國內還沒人對滬深300指數期權仿真交易市場的效率進行過系統的研究，本文將基于無風險套利的角度對我國滬深300指數期權仿真交易市場的效率進行開拓性的研究。考慮到目前股指期權只是仿真交易，其買賣和交割的都是虛假的資產，而股票市場和股指期貨市場是實際進行交易的市場，在目前情況下，跨市場之間的套利在實際操作中并不可行，而股指期權市場借助仿真交易系統有進行套利操作的可行性，因此本文主要將重點放在期權市場自身的有效性檢驗上。

二、模型

基于無風險套利的角度來研究市場效率需要同時涉及幾個不同的正在交易的期權合約。通過具有相同到期日的不同執行價格的看漲或看跌期權價格之間的關系來檢驗期權市場的效率，這種價格之間的關系可以通過構造出價差期權，然后比較價差期權的成本和收益的大小來實現，價差期權是收益有限同時損失也有限的期權組合。

（一）牛市價差條件

牛市價差期權可以通過買入一個具有較低執行價格X1的看漲（跌）期權和賣出一個具有較高執行價格的看漲（跌）期權組成（X1＜X2）。考慮買賣價差和交易成本后，在不存在套利機會的期權市場中，牛市價差期權滿足下列不等式：

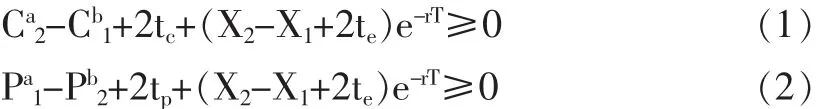
其中下標1和2表示期權的執行價格為X1和X2，C和P表示看漲期權和看跌期權，上標a和b表示期權的賣出價格和買入價格，tc和tp表示看漲期權和看跌期權的交易費用，te表示期權的行權費用，r是無風險利率，T是期權的到期時間。

上述不等式違反則意味著市場是無效的，存在無風險套利機會。違反（1）式的套利策略為買入執行價格為X2的看漲期權，賣出執行價格為X1的看漲期權，其到期無風險收益最小為X1-X2-2te+erT（Cb1-Ca2-2tc），違反（2）式的套利策略為賣出執行價格為X2的看跌期權，買入執行價格為X1的看跌期權，其到期無風險收益最小為X1-X2-2te+erT（Pb2-Pa1-2tp）。

（二）盒式價差條件

盒式價差期權是執行價格為X1和X2的看漲期權所構成的牛市價差與具有相同執行價格的看跌期權所構成的熊市價差的組合（X1＜X2）。考慮買賣價差和交易成本后，在不存在套利機會的期權市場中，盒式價差期權同時滿足下列不等式：

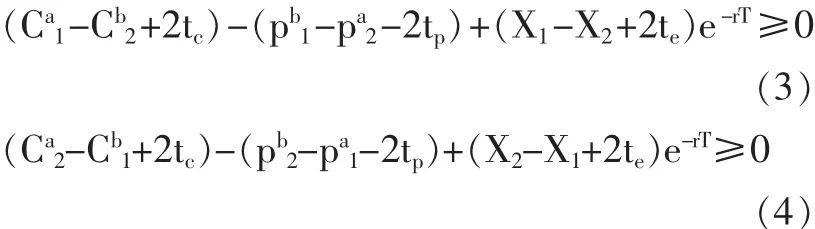
上述不等式違反則意味著市場是無效的，存在無風險套利機會。違反（3）式的套利策略為，買入執行價格為X1的看漲期權和執行價格為X2的看跌期權，賣出執行價格為X1的看跌期權和執行價格為X2的看漲期權，其到期的無風險收益最小為X2-X1-2te+erT（Pb1-2tp+Cb2-2tc-Ca1-pa2）。 違反（4）式的套利策略為，賣出執行價格為X1的看漲期權和執行價格為X2的看跌期權，買入執行價格為X1的看跌期權和執行價格為X2的看漲期權，其到期的無風險收益為X1-X2-2te+erT（pb2-pa1-2tp-Ca2+cb1-2tc）。

（三）蝶式價差條件

蝶式價差期權由3種具有不同執行價格的期權組成，可以分別用看漲期權和看跌期權組成，其構造方式為：買入1個具有較高執行價格看漲（跌）期權和1個具有較低執行價格的看漲（跌）期權，賣出2個具有中間執行價格的看漲（跌）期權。考慮買賣價差和交易成本后，在不存在套利機會的期權市場中，蝶式價差期權滿足下列不等式：

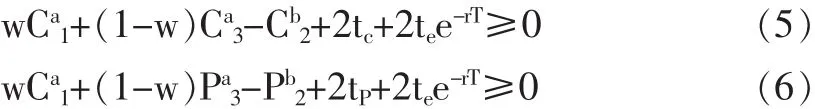
其中 X1＜X2＜X3，w=（X3-X2）/（X3-X1），違反（5）式的套利策略為買入w份執行價格為X1的看漲期權和（1-w）份執行價格為X3的看漲期權，同時賣出執行價格為X2的看漲期權，其到期的無風險收益最小為 erT（Cb2-wCa1-（1-w）Ca3-2te）-2te。 違反（6）式的套利策略為買入w份執行價格為X1的看跌期權和（1-w）份執行價格為X3的看跌期權，同時賣出執行價格為X2的看跌期權，其到期的無風險收益最小為erT（Pb2-wPa1-（1-w）Pa3-2tP）-2te。

三、分析方法

在利用歷史交易數據通過上述（1）到（6）式進行市場效率研究時，一般分為兩種分析方法，一種是事后分析（ex-post），一種是事前分析（ex-ante）。 本文也采用這兩種分析方法進行研究。

事后分析是對期權市場理論上的有效性進行分析，其假定在分析歷史交易數據時，如果無風險套利機會出現，則自發完成無風險套利，將理論上存在套利交易機會完全抓住，套利收益沒有任何風險。本文中為了解決數據的非同步性問題，只在報價時間相同的數據中進行匹配，數據匹配完成后，然后判斷是否存在套利機會。事后分析中采用持有到期策略，即套利組合一直持有到期權到期日，但由于分析所用的期權合約有的未到期，無法準確計算到期后的套利收益情況，為了能統一比較不同到期日股指期權的套利情況，本文計算得到的無風險收益是套利信號出現時，采用持有到期策略在期權到期時可以得到的最小的到期收益，在信號出現時的貼現值，持有到期時的套利收益的貼現值有可能大于上述數值。通過事后分析可以得到期權市場理論上有效性和最大的套利機會。在建立套利組合時，同一期權合約中的報價數據可以用在不同期權合約中，但固定的期權合約之間的報價數據匹配，每個合約的報價數據只能使用一次。

事前分析是對期權市場存在套利機會的套利可行性進行分析，套利信號出現后，與事后分析不同，套利組合的建立不是瞬時完成的，而是要延遲一段時間，這樣使得市場無效時所進行的套利就不再是無風險套利，市場效率的研究就更具有現實意義，如果理論上得到的套利機會在實際中不能利用，說明期權市場實際上還是有效的。事前分析中，考慮兩步進行，第一步是觀測套利的信號，信號的發現過程等同于事后分析部分，如果發現套利的信號，則執行第二步，通過套利策略建立套利組合。實驗中我們設置了套利組合建立的延遲時間，通過延遲時間的設置可以觀察市場效率隨時間的演變情況。本文中延遲時間分為 0～1秒、1～5秒、5～20秒三種情況，在事前分析中，我們假定延遲建立的套利組合的各個組成部分是同時建立，這樣消除套利組合未完全建立時受標的資產價格波動帶來的套利風險，從而可以單一地考察市場效率隨時間的演變情況。

四、數據

在研究期權市場的效率時，采用的數據通常有兩種類型，一類是日間數據，以每日的收盤價格作為判斷市場是否有效的依據，優點在于每日的數據容易得到，但由于時間間隔太大，數據量少，不能對市場的效率有較好的判斷，尤其對日內存在的高頻套利機會缺乏識別能力。在考慮買賣價差對套利的影響時，需要對交易數據進行處理，即在成交價格上加減0.5個買賣價差，得到對應于該成交價格的買賣報價，來消除買賣價差的影響。可見計算得到的買賣報價數據并不是真實的報價數據，可能會錯誤識別無風險套利機會，存在高估或低估套利交易收益的可能性。利用日間數據研究市場效率的學者不是很多。

另一類數據是日內數據，日內數據又可細分為兩種類型，一種是交易數據，如每筆的交易數據或者每分鐘的K線數據，一種是買賣報價數據。采用交易數據可以用來研究日內套利機會的存在性，但交易數據是已經完成交易的數據，套利機會存在時，不能直接用來建立套利組合。因此在利用交易數據進行研究時，在考慮買賣價差對套利的影響時，也需要對數據進行類似上節的處理，導致錯誤識別無風險套利機會，如Fung和Mok（2001）研究顯示高頻交易數據比買賣報價數據會低估套利機會的頻率和大小。

采用買賣報價數據可直接判斷套利機會的存在性，減輕無風險套利機會錯誤識別的可能，如果存在套利機會，可以方便地按照買賣報價建立套利組合，完全是市場真實情況的反映，這也是目前分析市場效率上采用最多的數據形式。

本文采用的數據為2014年8月1日至2014年9月30日，共兩個月每天的股指期權仿真交易的買賣報價數據，2014年8月和9月每天都有交易的滬深300指數期權有三種，到期日分別為2014年10月、12月和2015年3月。上述三種不同到期日期權在數據分析時間段，距離到期時間分別為17～77天、80～140天和171～213天，這樣三個不同到期日的期權將市場劃分為不同的時間段，為了描述方便，我們將上述三個到期日的期權分別稱之為近期、中期和遠期期權。期權買賣報價數據一般有5個價位，分別為買1到買5和賣1到賣5，本文選用的數據為買1和賣1報價數據，在分析時，我們去掉了買價或賣價為零的不合理的報價數據。

五、參數設置

（一）無風險利率的設置

無風險利率在期權市場的套利研究中是一個非常重要的參數，在該參數的選擇上，有的學者采用同業拆借利率，如Draper和Fung（2002）采用倫敦同業拆借利率（LIBOR），Fung 和 Mok（2001）采用香港銀行同行業拆借利率（HIBOR），有的學者采用國庫券收益率，如 Bharadwaj和 Wiggins（2001）利用美國財政部零息債券交易的賣出報價收益率作為無風險利率，Ackert和 Tian（2001）采用美國短期國庫券的收益率作為無風險利率。

與文獻類似，本文無風險利率也取自上海銀行間同業拆放利率（Shibor），Shibor是由信用等級較高的銀行自主報出的人民幣同業拆出利率計算確定的算術平均利率，具有很高的權威性和指導性，在市場化產品定價中得到廣泛運用。2014年8月1日的2個周、1個月、3個月、6個月和9個月的利率分別為4.0470%、4.2100%、4.7149%、4.9000%和4.9558%，為簡便起見，假定上述利率在8月份和9月份保持不變，其他時間的無風險利率通過線性內插得到。在進行套利交易時，根據期權到期日的長短，選用相對應到期日的無風險利率。

（二）其他參數設置

中金所規定，不論看漲期權還是看跌期權，股指期權合約交易手續費標準為每手5元，執行手續費為每手10元，因此tc=tp。參照國外成熟期權市場的經驗，對機構投資者來說，付息債券可以充當交易保證金，因此在本文的分析中，不考慮交易保證金的機會成本。

在（1）～（6）式中，出現的期權的價格和執行價格報價單位均為滬深300指數點，中金所規定合約乘數為每點100元人民幣，而期權的交易費用和執行費用的單位為人民幣，為了與期權的價格保持一致，需要進行折算，折算后每手的交易手續費和執行手續費分別為0.05點和0.1點。

六、結果與分析

（一）事后分析

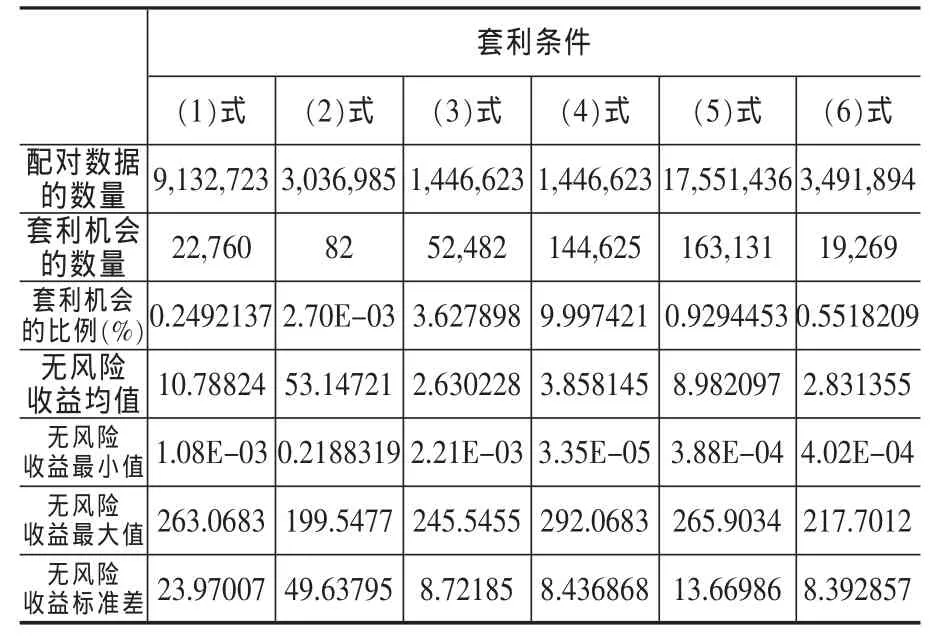
表1 期權市場有效性事后分析結果

從表1中的結果可以看出，我國的滬深300指數期權仿真交易市場確實存在著理論上的套利機會，但該套利機會不是很多。從三大套利條件來看，牛市價差條件套利可能性最少，套利機會的比例為0.25%和0.0027%，其次為蝶式價差條件，套利機會的比例為0.93%和0.55%，套利機會可能性最大的為盒式價差條件，比例為3.63%和10.0%。從套利機會的絕對數量來看，盒式價差和蝶式價差的套利機會數量較多，而牛市價差的套利機會數量較少，尤其是（2）式。

從期權類別來看，對比（1）式和（2）式，以及（5）式和（6）式，可以發現由于在滬深300指數期權仿真市場中，看漲期權的成交更為活躍，因此產生的配對數據數量也遠遠大于看跌期權，而且不管是從套利機會的數量還是從套利機會的比例來看，看漲期權都明顯大于看跌期權，尤其是牛市價差條件，（1）式套利機會的數量和比例是（2）式的上百倍。盒式價差條件同時包含了看漲期權和看跌期權，是一個跨期權類別的套利策略，結果顯示其套利機會的比例遠遠高于單一的看漲期權或看跌期權市場，說明跨期權類別的套利組合具有很大的套利潛力。

期權套利機會出現后，我們根據持有到期的套利策略計算了無風險套利的收益。從無風險收益的大小來看，除了牛市價差（2）式，其他套利條件的無風險收益的最小值變化不大。而無風險收益的最大值則相對變化不大，基本在200～300之間，最大值出現在盒式價差（4）式，最小值出現在牛市價差（2）式。從無風險收益標準差來看，盒式價差條件變動最小，蝶式價差居中，而牛市價差最大。而無風險收益的均值與標準差則相反，盒式價差收益均值最大，蝶式價差收益均值居中，而牛市價差收益均值最小。

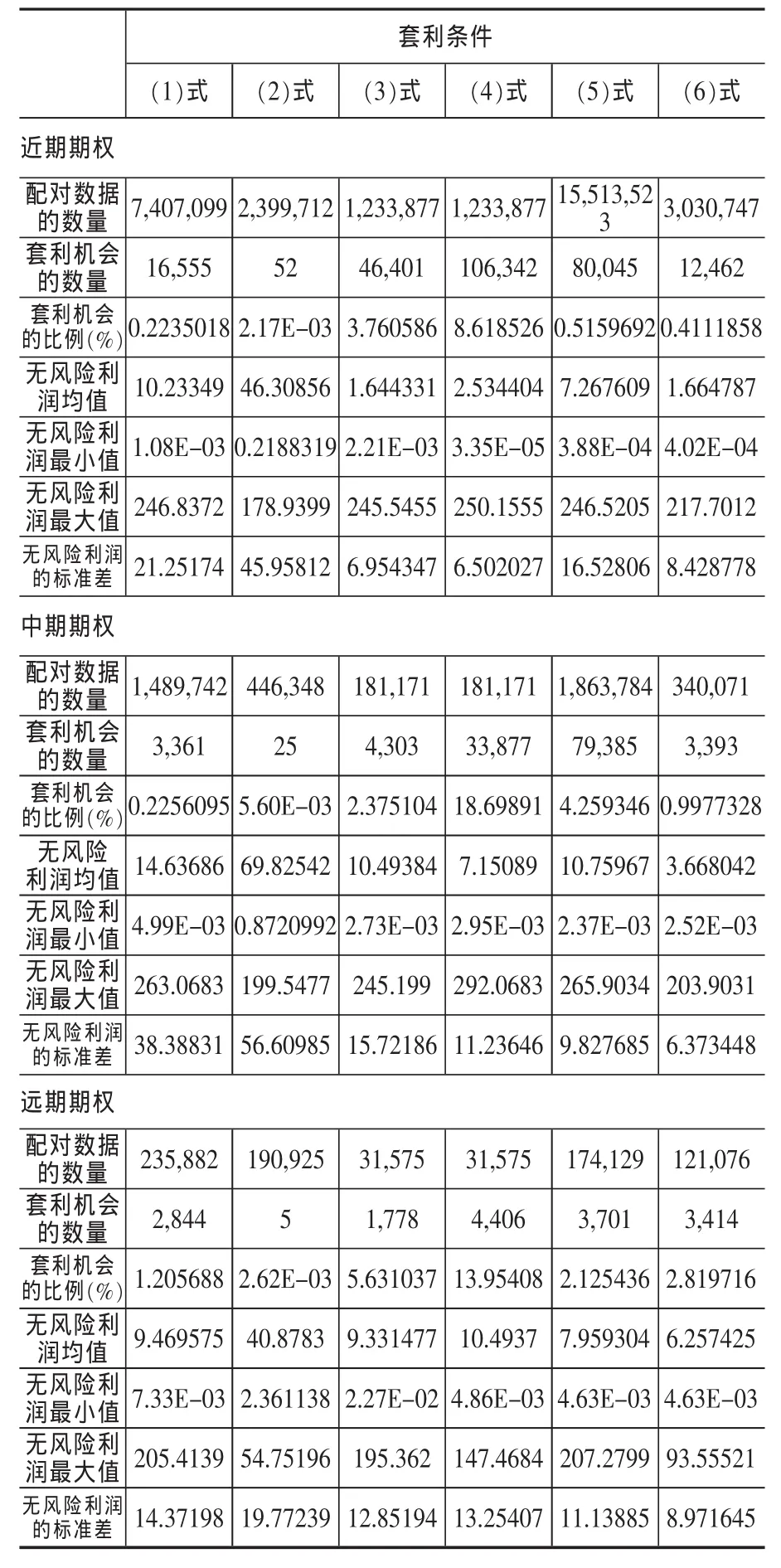
表2 不同到期日期權市場有效性事后分析結果

圖1 不同到期日期權市場的無風險收益標準差和均值散點圖

從表2中可以看出，近期期權的交易最活躍，產生的數據量也最多，遠期期權的交易最不活躍，產生的數據量最少。套利機會的比例盒式價差（4）式在近、中和遠期都遠遠大于其他五個套利條件，盒式價差（4）式在中期的套利機會比例接近20%，最低出現在近期，為8.6%，而其他五個套利條件基本位于0～5%之間。從時間的變化趨勢來看，六個套利條件的共同之處是遠期的套利機會比例都明顯大于近期的，而中期期權套利機會的比例則時高時低。從圖1中可以看出，無風險收益的均值和標準差呈現出一定的線性關系，具有明顯的正相關，收益均值除了牛市價差（2）式外，基本上遠期的大于近期。

（二）事前分析

1.牛市價差條件

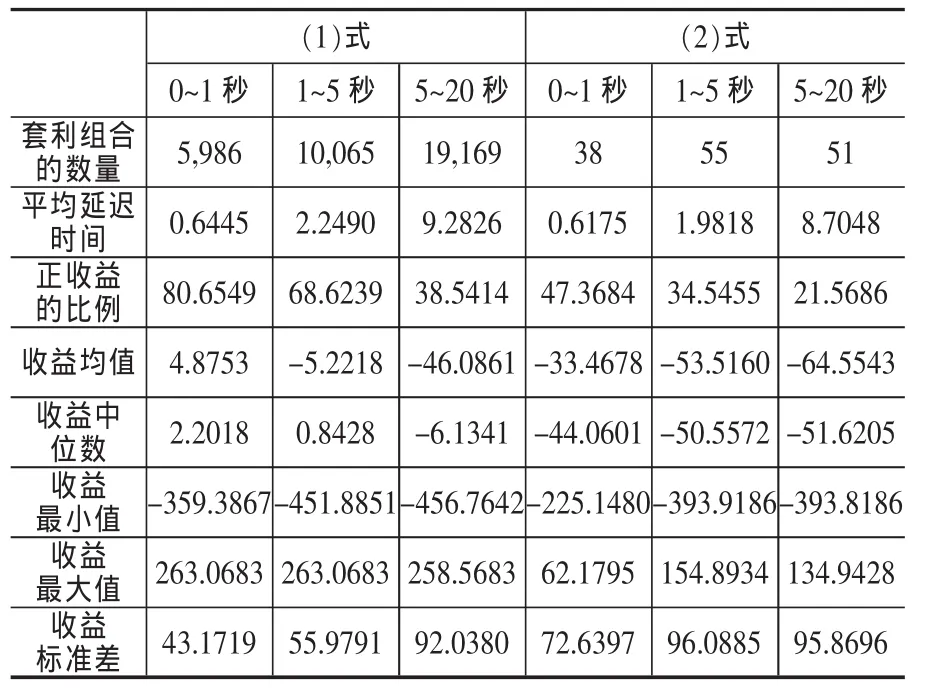
表3 牛市價差的事前套利情況

從表3的結果可以看出，看漲期權的牛市價差條件在延遲時間小于1秒時，可以取得正的套利收益，均值為4.88，正收益的數量幾乎是負收益數量的4倍，此時進行看漲期權的套利交易有利可圖。當延遲時間位于1～5秒內，套利組合建立的平均延遲時間增加到2.25秒時，其正收益的比例下降到70%以下，收益的均值也小于零，只有收益中位數還大于零，此時再進行期權的套利交易已經無利可圖，市場趨于有效。當平均延遲時間繼續增加到9.28秒時，其正收益的比例迅速下降到50%以下，收益均值和中位數都小于零，市場的有效性繼續增加。從收益分布的對稱性來看，在0～1秒內均值大于中位數，呈右偏分布，當時間繼續增加時，收益均值小于中位數，此時呈現左偏分布。總的來看，看漲期權市場在牛市價差條件下的無效性維持的時間很短，市場的無效性可以很快被糾正。

看跌期權的牛市價差套利不管延遲時間的長短，其正收益比例都小于50%，收益均值都小于零，并且隨著延遲時間的增加，其正收益的比例也迅速降低，可見看跌期權市場的牛市價差條件沒有套利機會，市場相對有效。

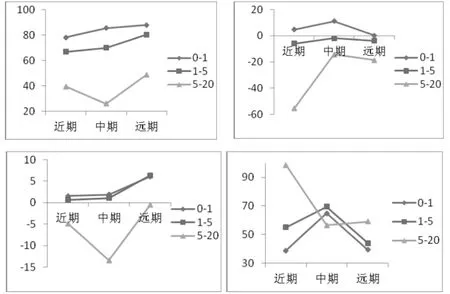
圖2 不同到期日看漲期權牛市價差的事前套利情況

與表3的情況相類似，圖2a中看漲期權市場隨著延遲時間的增加，其牛市價差套利正收益比例迅速下降，0～1秒內隨著期權到期日的增加，正收益的比例也增加，說明交易不活躍的看漲期權市場存在牛市價差套利機會較多，而活躍市場存在的套利機會較少。圖2b收益均值中，只有延遲時間小于1秒的情況下，其利益均值大于零，存在套利機會，其他延遲時間段則不存在套利機會。圖2c中在小于5秒的時間段內，收益中位數大于零，且隨期權到期日增加，說明遠期期權中極端負值出現的概率較大。圖2d中0～1秒和1～5秒收益標準差變化趨勢相同。不同到期日的看跌期權牛市價差樣本數量太少，因此不做具體分析。

2.盒式價差條件

表4 盒式價差的事前套利情況

表4中盒式價差正收益比例相對較高，在5～20秒范圍內，該比例仍然高于68%，在平均執行延遲時間超過6分鐘（300秒～1200秒段內）后，其正收益的比例才下降到50%以下。但收益的均值很小，1～5秒內僅有0.14和0.06，其后隨著延遲時間的增加，迅速小于零，與牛市價差相比，盒式價差的最小值更小，而從收益中位數和收益均值的關系來看，各個時間段內均值都小于中位數，說明收益呈現左偏分布。 從公式（3）式和（4）式對比來看，在 0～1秒和1～5秒內雖然后者的平均延遲時間大于前者，但仍具有較高的正收益比例和收益中位數，由于較大負值出現的頻率太高，導致其收益均值小于前者。

表5結果顯示，在不同到期日期權上，盒式價差的收益正比例隨到期日的增加下降較為緩慢，且近期和中期期權的比例明顯高于遠期，該點與牛市價差完全不同。盒式價差只在近期期權上0～1秒內套利收益均值大于零，隨著到期日的增加，其收益均值逐漸下降，說明近期市場很短的時間內存在一定的套利機會。此外，套利收益標準差也隨著期權到期日的增加而明顯增加，隨著延遲時間的增加而明顯增加。

3.蝶式價差條件

表5 不同到期日期權盒式價差的事前套利情況

從表中的結果可以看出，蝶式價差在看漲期權和看跌期權市場的差別很大，在時間較短的情況下，雖然看漲期權發出的套利信號數量明顯多于看跌期權，但最后形成的套利組合數量卻遠遠小于看跌期權，說明套利機會相對較多，在延遲時間為7.46秒時，其正收益的比例仍大于50%，不同時間段的最大套利收益也遠遠大于看漲期權，與事后分析結果差異較大。正收益比例上的差異導致兩者的收益均值差別很大，但都明顯小于零，說明市場都相對有效，但看漲期權的有效性要高于看跌期權。此外，在收益的標準差上，看漲期權明顯高于看跌期權。兩者的共同之處在于，蝶式價差套利收益的最小值的絕對值明顯大于最大值，與盒式價差相類似。

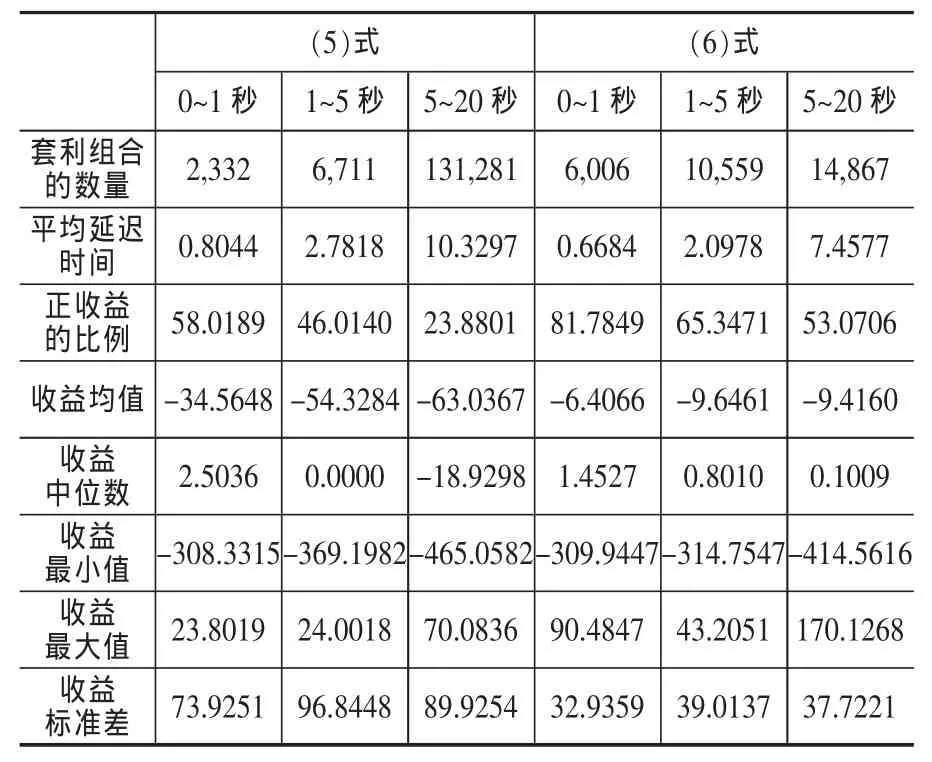
表6 蝶式價差的事前套利情況

與表6結果相似，表7結果顯示，從正收益比例、收益均值、收益中位數和收益標準差來看，蝶式價差在看漲期權和看跌期權市場上差別很大。看漲期權蝶式價差最多的套利機會出現在遠期看漲期權上，此時收益均值也最大，而看跌期權蝶式價差在近期套利機會最多，此時收益均值最大。總的來說，蝶式價差在不同到期日的看跌期權和看漲期權上都不存在套利機會，相對來說，近期期權市場上看跌期權的套利機會多于看漲期權，而在遠期期權上，則恰好相反。

七、結論與展望

本文基于無風險套利的角度，利用2014年8～9月期權交易的買賣報價數據，采用事前和事后分析的方法對我國滬深300指數期權仿真交易市場的效率進行了開創性研究，得到如下結論：

在事后分析中，結果顯示我國的滬深300指數期權仿真交易市場的買賣報價數據中確實存在著理論上的套利機會，但套利機會較小。從套利機會的可能性來看，牛市價差條件套利可能性最小，其次為蝶式價差條件，最大的為盒式價差條件，而無風險收益的順序則相反。從時間的變化趨勢來看，遠期期權的套利機會比例都明顯大于近期的，此外，收益的均值和標準差呈現出具有明顯的正相關性。

事前分析則與事后分析結果不一致，盒式價差條件和看漲期權牛市價差條件在0～1秒內套利收益均值大于零，存在有效的套利機會，而其他套利條件則不存在有效的套利機會，但延遲時間超過1秒后，買賣報價仍維持套利機會的可能性迅速降低，市場逐漸趨向有效。從不同到期日期權市場來看，牛市價差條件在交易不活躍的看漲期權市場存在套利機會較多，在活躍市場存在的套利機會較少，盒式價差條件則相反，在活躍的期權市場中存在的套利機會多，而蝶式價差介于兩者之間，在不活躍的看漲期權市場中套利機會多，在不活躍的看跌期權市場中套利機會少。

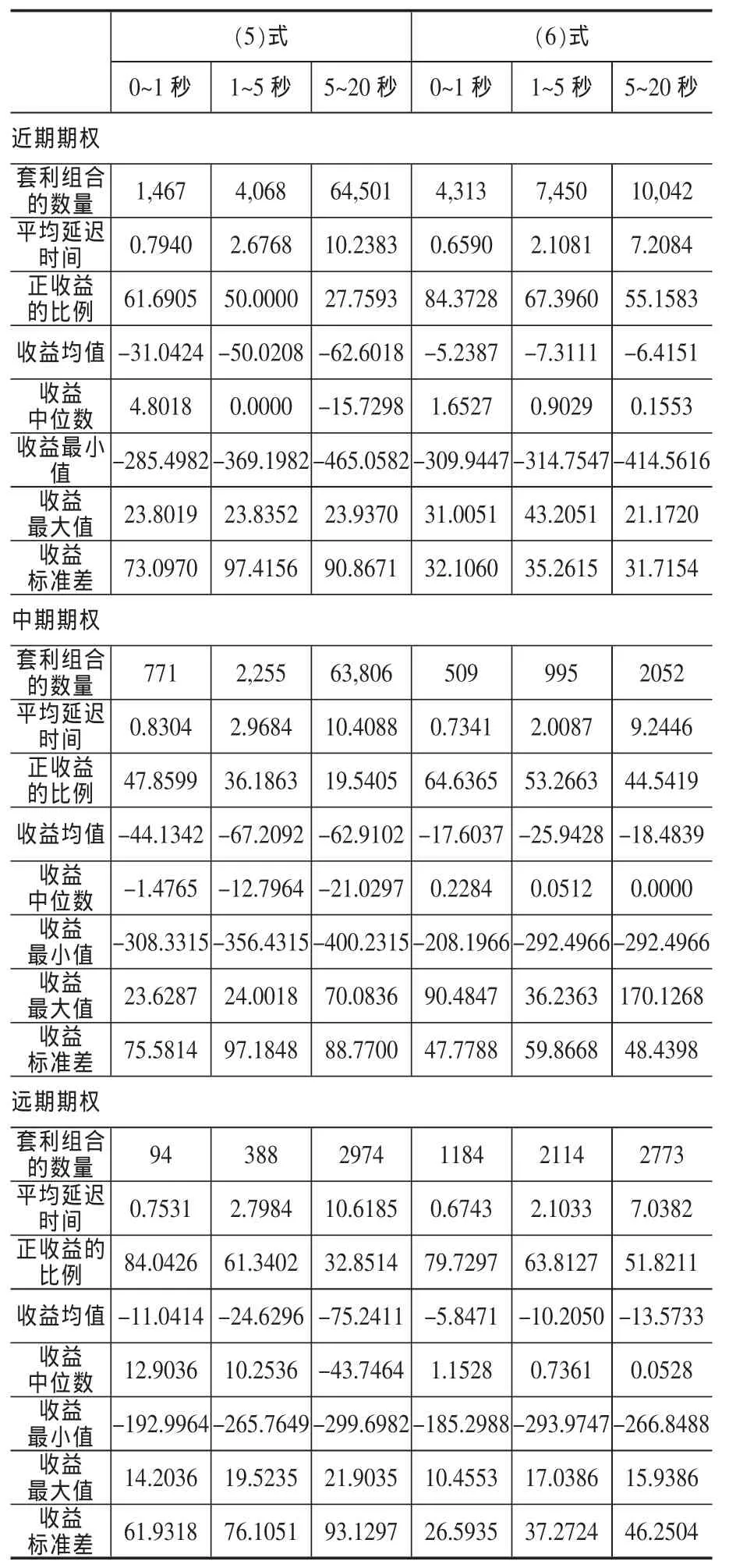
表7 不同到期日期權蝶式價差的事前套利情況

綜上所述，雖然目前的滬深300指數期權為仿真交易，但期權市場已經具有了一定的有效性，說明了目前的仿真期權合約和交易機制的設計是相對合理的。本文提供的股指期權市場效率檢驗的方法和思路同樣可以用在股票期權上，2015年2月9日，上證50ETF期權作為我國第一只股票期權，已在上海證券交易所正式上市交易，以后隨著我國上海交易的股指期權和股票期權數量逐漸增多，可以預見該方法的應用將越來越廣。

[1]Evnine J,Rudd A.Index options:the early evidence[J].The Journal of Finance,1985,40(3):743～756.

[2]Ackert L E,Tian Y S.The introduction of Toronto index participation units and arbitrage opportunities in the Toronto 35 index option market[J].The Journal of Derivatives,1998,5(4):44～53.

[3]Kamara A,Miller T W.Daily and intradaily tests of European put-call parity[J].Journal of Financial and Quantitative Analysis,1995,30(04):519～539.

[4]Brunetti M,Torricelli C.Put–call parity and cross-markets efficiency in the index optionsmarkets:evidence from the Italian market[J].International Review of Financial Analysis,2005,14(5):508～532.

[5]Draper P,Fung J K W.A study of arbitrage efficiency between the FTSE-100 index futures and options contracts[J].Journal of Futures Markets,2002,22(1):31～58.

[6]Fung JKW,Mok H M K.Index options-futures arbitrage:a comparative study with bid/ask and transaction data[J].Financial Review,2001,36(1):71～94.

[7]BrunettiM,Torricelli C.The internal and cross market efficiency in index option markets:an investigation of the Italian market[J].Applied Financial Economics,2007,17(1):25～33.

[8]Vipul.Box-spread arbitrage efficiency of Nifty index options:the Indian evidence[J].Journal of Futures Markets,2009,29(6):544～562.