高中數學解題教學中“通法”與“特技”的探析

☉江蘇省黃橋中學 袁春偉

高中數學解題教學中“通法”與“特技”的探析

☉江蘇省黃橋中學 袁春偉

高中數學解題教學是數學課程教學的重要組成部分，數學解題方法一直是教師和學生關注的焦點，解題方法的優劣某種程度上決定著解題的速度與效率.筆者從事高中數學教育教學多年來，一直注重和加強數學解題中“通法”的訓練，實踐表明：運用“通法”進行解題固然重要，但是解題過程中隱含的“特技”也是值得注意的，在此總結如下.

一、靈活運用“通法”中體現的一般規律，獲取“簡解”之“特技”

處理具體問題的基本策略通常習慣于遇“繁”則去思考“簡”的處理方法，高中數學解題也是同樣的道理.然而，簡解來源于對基本處理方法的調整與深層次的思考，發現簡解、特技的過程也是思維轉換能力提升的過程.

例1函數f（x）=ax2+（2a-1）x+1在上存在最大值3，試求實數a的值.

點評：本題通常的處理手段都是采取分類討論的思想，利用這種通法，正常情況下都要針對系數a的正負進行討論，要探究拋物線的開口方向，同時還要探究對稱軸與題中所給區間之間的關系.如果拋物線開口向上，對稱軸在區間內的情況下，還要分析對稱軸與區間兩端點之間的距離遠近情況，利用這種通法解題，大約有7種情況要討論，求解過程中容易手忙腳亂，出錯率較高.上述呈現的解法來源于在通法討論的過程中，經過細心的觀察發現二次函數在閉區間上一定存在最值，取得最值的點可能是區間的兩端點或者拋物線的對稱軸的頂點處，由此我們不難發現試題背后的一般規律，進行合理思維方向的轉換，利用代入驗證的方法進行解題，結果清晰、易懂.

二、在“通法”中揭示問題的本質，形成“巧解”之“特技”

高中數學解題教學中，對于“通法”的加強是毋庸置疑的，但是過分的強調容易讓學生產生思維定勢，產生負遷移現象，嚴重影響正確解題的效率.

例2證明以下4題.

剖析：數學歸納法可以說是高中數學證明題中常用的一種“通法”，高中學生能夠利用數學歸納法順利完成題1和題2兩道試題的證明.題3與題4其實是題1和題2簡單的演變題而已，但是很多學生難以解決，主要是學生仍然利用數學歸納法即“通法”處理，當n=k+1時不等式左側比n=k時增加一個正項，直接推導無法完成證明，學生的思維受到阻礙.若我們在利用歸納法處理題1的過程中發現：此式是題1中不等式成立的基礎，借助此式可以思考運用“放縮裂項法”尋求到解決題1的簡易方法，進而快速解決題3.學生對題4不知從何處下手的原因是沒有準確把握問題的本質，其實只要認真思考數學歸納法的常規推理過程，不難發現問題的本質是：f（k+1）＜f（k），借助函數的單調性巧妙處理題2，同時可以發現題4的本質為，則存在最小整數t=8，使得

三、在準確挖掘與捕捉隱含信息的過程中，發現“巧解”之“特技”

高中數學多數試題中存在著豐富的隱含信息，對這些隱蔽信息的挖掘和捕捉往往是解題的關鍵因素，特別是在解題過程中能夠有效簡化運算過程，便于學生發現處理難題的“特技”.

解析：根據題意構建如圖1所示的橢圓，由幾何關系可知：橢圓上的點到準線y=1的距離介于最小值|A1M|與最大值|A2M|之間；橢圓上的點P（0，1）距離準線y=1的垂直距離為2，則|A1M|≤2≤ |A2M|，即

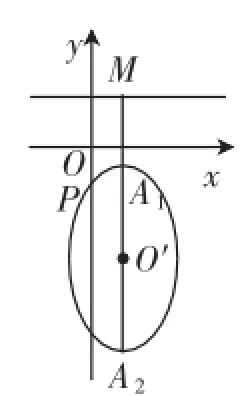
圖1

點評：本題的常規處理手段是將已知點代入橢圓方程，與第二定義的相關知識互相結合進行求解，可謂“通法”，解題過程比較復雜.實際上，如果能有意識地捕捉橢圓中的特定性質這一信息，充分利用點在橢圓上這一幾何條件，完全可以實現上述所呈現的“巧解”，解析中|A1M|≤2≤|A2M|正是深入捕捉信息所得到的結果.

四、在針對數學命題的多途徑等價轉換中，悟出“簡解”之“特技”

高中數學解題過程實質上是不斷地將命題由繁到簡、由難到易、由生到熟的轉化過程.實踐證明，對數學命題進行多途徑的等價轉換，能夠從中悟出“簡解”.

例4已知f（x）=2x+a的反函數的圖像上存在三點A（x+a，y1）、B（x，y2）、C（2+a，y3），僅存在一個實數x，使得y1，y2，y3成等差數列，試求實數a的取值范圍.

剖析：根據題意，反函數的表達式為y=log2（x-a），則y1=log2x，y2=log2（x-a），y3=log22=1，則問題轉化為：2y2=y1+ y3，即方程2log2（x-a）=log2x+1存在唯一解.

如果直接對（Ⅰ）進行討論，結果相當復雜.但是如果仔細觀察不難發現（3）式可以由（1）與（2）得到，則（Ⅰ）可以等價于：（Ⅱ）則原命題中涉及的問題可以有如下幾種簡化途徑.

途徑1：等價轉化為求方程（4）僅有一個大于實數a的解時a的取值范圍；

途徑2：等價轉化為求f（x）=（x-a）2（x＞a）與g（x）=2x的圖像有唯一公共點時實數a的取值范圍.

總而言之，作為一線的高中數學教師，在平時的解題教學中，在強調“通法”解題教學的同時，應該重視引導學生在運用、回顧“通法”的過程中，注意觀察、思考與分析，從中悟出“特技”的處理策略，有效揭開“特技”背后的神秘面紗，不僅激發學生的學習興趣，而且提升學生運用數學知識處理實際問題的能力.A