新課程建構(gòu)模式下的試題講評初探

☉浙江省余姚市第二中學(xué) 楊福來

新課程建構(gòu)模式下的試題講評初探

☉浙江省余姚市第二中學(xué) 楊福來

眾所周知，數(shù)學(xué)教學(xué)是概念教學(xué)—新知教學(xué)—解題教學(xué)—反饋教學(xué)—反思教學(xué)等一系列系統(tǒng)的教學(xué)綜合．對整個高考應(yīng)試而言，學(xué)生更直接領(lǐng)會的是解題教學(xué)的好壞，這就要求教師在解題教學(xué)中準(zhǔn)確實施試題講評．在國內(nèi)著名的數(shù)學(xué)論壇K12或百度貼吧里，筆者常常看到學(xué)生的抱怨：我們的老師講什么都不知道，明明很簡單的問題講的方法又繁又復(fù)雜！老師講的方法我聽懂了，可是我們根本想不到！怎么破？……這就表明了解題教學(xué)中很重要的一個問題：教師在試題講評的時候如何做到以生為本？試題講評如何在新課程理念下讓學(xué)生積極參與？如何在傳統(tǒng)的試題講評基礎(chǔ)上做到螺旋式上升？筆者認(rèn)為，這是教師關(guān)于試題分析教學(xué)部分一個值得全新研究的視角．

課程標(biāo)準(zhǔn)的理念一直致力于學(xué)生的自主探索和積極建構(gòu)，其特別提到了數(shù)學(xué)教學(xué)如何盡可能地去形式化，如何通過對特殊情形的認(rèn)知到達(dá)一般化的歸納，如何滲透主動建構(gòu)知識體系的操作等.從近年的新課程教學(xué)來看，在概念教學(xué)、新知教學(xué)等方面我們做出了很多類似的嘗試和探索，在各種公開課中也聆聽了許多這樣的探求．但是筆者思考：似乎在復(fù)習(xí)課、解題課、試題分析課等環(huán)節(jié)，教師對新課程理念的合理運(yùn)用和滲透并不如新知教學(xué)那么普遍，這一點(diǎn)很多教師都有共識．究其原因，筆者認(rèn)為有三：其一，試題講評、復(fù)習(xí)教學(xué)等課程的設(shè)計不如新知教學(xué)方便，尤其在利用情境手段引導(dǎo)學(xué)生發(fā)現(xiàn)、挖掘情境背后的形式化結(jié)果方面，試題講評、復(fù)習(xí)教學(xué)難度較大，這也是此類課開設(shè)不夠普遍的原因；其二，教師自身的觀念限制和能力限制，我們知道教師在解決問題時存在知識主觀的熟練程度和習(xí)慣不同，造成了其解決問題往往從自身思考角度入手，有時這種思考角度并非是學(xué)生能夠入手的思考方向和著力點(diǎn)，致使試題講評未能緣自學(xué)生的思維發(fā)展區(qū)出發(fā)，有些事半功倍；其三，觀念的更新，新課程一直提倡教師專業(yè)化的成長，而不再是做一個普普通通的教書匠混日子，要有更出色的教學(xué)能力和授課水平，必須在學(xué)生最為重視的試題分析上做到潛心研究，提高自身專業(yè)化的發(fā)展．陜西師大羅增儒教授在關(guān)于如何解題、析題時說：當(dāng)下數(shù)學(xué)教學(xué)的核心依舊是解題教學(xué)，因此試題的分析能力、解決問題的能力是辨別教師水平最直接的體現(xiàn)，我建議要用新的方式、方法去引導(dǎo)中學(xué)生解決數(shù)學(xué)問題，這里的方法可以是一題多解、啟發(fā)式講學(xué)、錯題辨析等多種不同的手段進(jìn)行嘗試．本文鑒于上述緣由和數(shù)學(xué)解題教學(xué)泰斗羅教授的分析，從試題分析多種方式的探索，結(jié)合新課程理念做了一些初探，與大家交流．

一、花出深谷，其香尤濃——學(xué)生思維視角講評

解決某個數(shù)學(xué)問題有很多方法，教師在試題解決過程中首要考慮的是方法的簡便性、運(yùn)算復(fù)雜程度等，有時正是因為考慮上述環(huán)節(jié)過多導(dǎo)致忽視了學(xué)生解決問題的心理機(jī)制.我們常常有這樣的感受：教師將自己的方式、方法在黑板上積極板演，講得頭頭是道，最后學(xué)生往往沒有吸收進(jìn)去，而且其自己的方法也沒有弄明白，這樣的試題講評是低效的、無效的．尊崇新課程理念，筆者認(rèn)為試題講評還需要從學(xué)生的學(xué)情出發(fā)，首先通過批閱查看學(xué)生對解題方法使用的分布率，其次是思考學(xué)生為何會產(chǎn)生如此的想法解決問題，最后是通過學(xué)生思維的視角與學(xué)生一起分析試題、解決試題，這樣的教學(xué)是有生命力的，符合學(xué)生看問題的角度，符合新課程鼓勵學(xué)生探索、積極建構(gòu)方法解決問題的理念．

案例1：如圖1，過x軸上一動點(diǎn)A（a，0）引拋物線y=x2+1的兩條切線AP、AQ，P、Q為切點(diǎn)，設(shè)切線AP、AQ的斜率分別為k1和k2．

（1）求證：k1k2=-4；

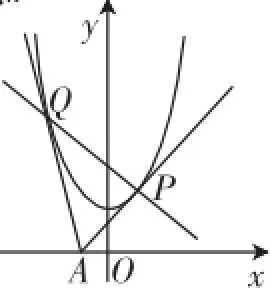
圖1

（2）試問：直線PQ是否經(jīng)過定點(diǎn)？若是，求出該定點(diǎn)的坐標(biāo)；若不是，請說明理由.

說明：本題是解析幾何中直線與拋物線位置關(guān)系的一種典型問題，考查了拋物線的切線、動直線過定點(diǎn)的問題.筆者將本題布置為某次作業(yè)，在批閱過程中發(fā)現(xiàn)學(xué)生解決問題的思維視角與教師的想法有些出入，因此筆者研究學(xué)生對于本問題的解答思路后進(jìn)行了課堂試題的學(xué)生視角講評.

第一問講評如下所示.

本題是研究拋物線的切線，考慮到還未對導(dǎo)數(shù)進(jìn)行授課，因此導(dǎo)數(shù)知識運(yùn)用暫不予考慮.

學(xué)生視角講評1：設(shè)過A（a，0）與拋物線y=x2+1相切的直線的斜率是k，則該切線的方程為：y=k（x-a）.

學(xué)生視角講評2：設(shè)點(diǎn)P（x1，y1）、Q（x2，y2），在這兩點(diǎn)處的切線分別為l1、l2.設(shè)l1：y-y1=k1（x-x1）.由

由題意知l1、l2交于點(diǎn)A（a，0），所以

學(xué)生視角講評3：設(shè)過A（a，0）與拋物線y=x2+1相切的直線的斜率是k，則該切線的方程為：y=k（x-a）.

說明：為何講評第一問的解法呢？筆者發(fā)現(xiàn)：學(xué)生對于相切的認(rèn)知永遠(yuǎn)是最直白的接受和表達(dá)——Δ=0，對根的認(rèn)知也非常直接——求根公式求之，因此講評1是最尊崇學(xué)生思維角度的講評，也是最容易靠攏學(xué)生思維的講評；講評2借鑒了通過導(dǎo)數(shù)求拋物線的切線方程的思想，通過設(shè)切點(diǎn)坐標(biāo)，聯(lián)立方程后的判別式為0，從而得到切線方程的斜率，計算量較大，但是為解決第二問做好了充分的準(zhǔn)備；講評3是僅有的少數(shù)優(yōu)秀學(xué)生的視角，但應(yīng)該是本題最簡化的視角，教師應(yīng)該將這一優(yōu)秀學(xué)生的視角予以呈現(xiàn)，用韋達(dá)定理解之是本問題最簡捷的方向.

第二問講評如下所示.

研究直線過定點(diǎn)是如何實現(xiàn)的？從最基本的知識可以知道，帶有一個參變量的直線方程可以研究其過定點(diǎn)，因此講評的核心是如何將直線PQ表示為關(guān)于變量a的直線.在學(xué)生解決的過程中，筆者整理了三種不同的方式予以講評.

學(xué)生視角講評3：設(shè)P（x1，y1）、Q（x2，y2），故切線AP的方程是，切線AQ的方程是又由于A點(diǎn)在AP、AQ上，則y2=2x2a+2，則直線PQ的方程是y=2ax+2，則直線PQ過定點(diǎn)（0，2）.

說明：通過批閱發(fā)現(xiàn)，學(xué)生解決本題最易想到的視角是利用設(shè)點(diǎn)—求斜率—寫出直線—研究定點(diǎn)，因此視角1與視角2都是按照學(xué)生在閱卷中的想法進(jìn)行的講評，視角3只有少數(shù)優(yōu)秀學(xué)生考慮使用，其合理地借鑒了“過圓外一點(diǎn)作兩條切線，則兩切點(diǎn)連線所在的直線方程”的推導(dǎo)過程進(jìn)行了類比處理，是思維較為高端抽象的一種體現(xiàn)，教師講評視角3是為了提攜學(xué)生站在更為抽象、有高度的角度看問題．

二、探索建構(gòu)，悠然自得——啟發(fā)引導(dǎo)視角講評

在突出學(xué)生解決問題方面，筆者認(rèn)為要加強(qiáng)學(xué)生問題解決的探索能力的培養(yǎng)，在試題講評中引入學(xué)生探索、建構(gòu)、講評，將試題講評交還給學(xué)生，使其真正領(lǐng)悟到講清楚問題比會解問題更容易將知識在自身體系中完善起來．看一個案例.

案例2：設(shè)命題p：方程（m-6）x2+（m+6）y2=1表示雙曲線；命題q：方程x2+y2-2x+4y+m=0表示的曲線是圓．

（1）當(dāng)m=5時，判斷命題“p且q”的真假，并說明理由；

（2）若命題“p或q”為真命題，求實數(shù)m的取值范圍．

說明：本題是筆者給予學(xué)生講評嘗試的一道數(shù)學(xué)問題，主要是請學(xué)生研究了第二問，從邏輯認(rèn)知的角度使其認(rèn)清楚“或”結(jié)構(gòu)的命題是如何講評的，請學(xué)生探索建構(gòu)．

學(xué)生探索建構(gòu)1：我認(rèn)為，若命題p為真命題，則-6＜m＜6，若命題p為假命題，則m≤-6或m≥6；若命題q為真命題，則m＜5，若命題q為假命題，則m≥5.因為命題“p或q”為真命題，所以分p真且q假，或p假且q真，或p真且q真三種情況，即解得m＜6．

學(xué)生探索建構(gòu)2：我認(rèn)為可以從反面認(rèn)知本問題.若命題“p或q”為假命題，則p假且q假，m≥6，所以當(dāng)命題“p或q”為真命題時，m＜6．

學(xué)生探索建構(gòu)3：我想在第一位同學(xué)的解答中簡化就可以，因為命題“p或q”為真命題，所以p和q中至少有一個是真命題，即-6＜m＜6或m＜5，解得m＜6．

說明：第一位同學(xué)的解題思路凸顯了大部分學(xué)生的思路，即將問題分析清楚，分類討論必須不重、不漏，進(jìn)而達(dá)到目的；第二位同學(xué)思維敏捷，考慮到問題的分類比較煩瑣，因此利用哲學(xué)思想“正難則反易”，從反面突破；第三位同學(xué)的認(rèn)知水平要高于前兩位，解決“或”命題何必一定要不重、不漏地分類呢？顯然這位同學(xué)已經(jīng)清晰地認(rèn)知了問題，進(jìn)而簡化了分析和解答．

三、再上層樓，望盡天涯——思想方法視角講評

講評問題的最高境界在于引導(dǎo)學(xué)生從問題中管窺到思想方法的使用，我們知道數(shù)學(xué)思想才是高中數(shù)學(xué)最終給予學(xué)生教學(xué)最高端的層次，有了思想方法，學(xué)生解決問題不再拘泥于技巧，數(shù)學(xué)學(xué)習(xí)的眼界和問題解決的思考都能望盡天涯，再上層樓．

說明：通過簡單的換元思想，結(jié)合數(shù)形結(jié)合思想，將問題轉(zhuǎn)換為二次函數(shù)問題解決，對學(xué)生而言，這種問題的處理在于講評時思想方法的滲透．

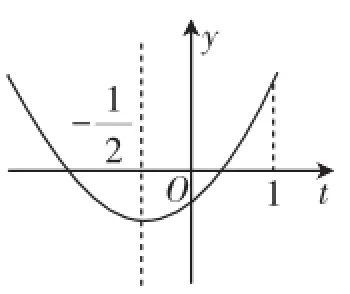
圖2

說明：講評此類含參數(shù)的三角、指數(shù)、對數(shù)等復(fù)雜方程解的問題，通常有兩種處理思路：一是分離參數(shù)構(gòu)建函數(shù)，將方程有解轉(zhuǎn)化為求函數(shù)的值域；二是換元，將復(fù)雜方程轉(zhuǎn)化為熟悉的二次方程，進(jìn)而利用二次方程解的分布情況構(gòu)建不等式或構(gòu)造函數(shù)加以解決．本題正是以典型的問題引導(dǎo)學(xué)生對“有解”型問題的處理，增加其解決問題的經(jīng)驗．?dāng)?shù)學(xué)思想方法的學(xué)習(xí)和運(yùn)用是一個潛移默化的過程，是在多次領(lǐng)悟、反復(fù)應(yīng)用的基礎(chǔ)上形成的．作為教師，應(yīng)盡可能多地為學(xué)生創(chuàng)造條件讓學(xué)生實踐運(yùn)用數(shù)學(xué)思想方法來解題，通過實踐活動中主體（學(xué)生）對客體（問題）的認(rèn)知結(jié)構(gòu)不斷的構(gòu)建過程，促進(jìn)學(xué)生數(shù)學(xué)思想的發(fā)展．試題講評是很好的總結(jié)、回顧、強(qiáng)化，在運(yùn)用數(shù)學(xué)思想方法上肯定能得到“升華”．

總之，試題講評有了新時代的發(fā)展，不同于以往將問題隨隨便便解答即可的地步．本文從三個層面做了一定的闡述，限于水平有限，懇請讀者提出批評指正，共同研究和深化．

1.朱永祥.再談數(shù)學(xué)思想方法的挖掘和應(yīng)用［J］.中學(xué)數(shù)學(xué)（上），2008（2）.

2.羅先禮.數(shù)學(xué)教學(xué)的實踐與思考［J］.中小學(xué)數(shù)學(xué)（高中版），2008（12）.

3.展國培.有效教學(xué)，從關(guān)注學(xué)生開始［J］.中小學(xué)數(shù)學(xué)（高中），2013（1）.A