數學課堂中的“逆勢而為”

謝家文

一、在“逆例（型）”中導入，培養逆向思維意識

大部分數學知識有著一定的生活原型，教師喜歡在新授教學的導入環節尋找生活原型，創設有明顯生活原型的教學情境，喚醒學生已有的生活體驗，試圖拉近知識與學生的距離，讓學生學得輕松而精彩。其實有不少生活原型，學生本來很熟悉了，課堂上還利用它們，學生容易熟視無睹，不但提不起興趣，也難以引發他們對生活原型的真正思考。如果此時能逆著生活原型創設情境，就會產生認知沖突，吸引他們往深層次思考。

例如，“軸對稱圖形”一課的教學。一位教師并沒有戴著生活中兩邊大小一樣的眼鏡進入課堂，而是一大一小，與生活原型不同。全班一片笑聲，笑聲過后，教師問道：“為什么笑？”學生說：“兩邊大小不一樣，很滑稽。”教師追問：“怎么知道不一樣？你能用什么方法證明嗎？”學生反饋：“把眼鏡對折。”教師又步步緊逼：“如果眼鏡不能對折呢？”經過學生的討論，最終得出：“把它們放在紙上描畫出來，就可以對折。”教師順勢引出概念：“如果一個圖形沿著一條直線對折后兩部分完全重合，這樣的圖形就叫作軸對稱圖形。”軸對稱圖形的產生過程就這樣一步步地呈現出來。這里得益于教師創造了一個不對稱的生活實例，引發學生認知沖突，從而很自然地抽象出軸對稱圖形的本質特征，形成概念。在數學教學中多一些逆向的生活實例引入新課，不但能引發認知沖突，深化認知，還能培養學生對生活中習以為常的生活現象、生活例子多一些逆向的眼光，從而培養逆向思維意識。

二、在逆思中新授，培養逆向思維意識

先入為主——先聽進的話或先獲得的印象，往往在頭腦中占主導地位。此話映射在教學上就是——教師新授時的思維方向對學生的思維意識起著舉足輕重的作用。為此，在新授時，筆者會思索例題教學思路的互逆性，時常會引導學生逆向思考例題的解題思路，以訓練學生的逆向思維意識。

例如，在教學習題：“成人票24元，兒童票半價。星期天，爸爸媽媽帶著玲玲去‘冰雪天地游玩。購門票需要花多少錢？”常用的正向思維是：“爸爸的票錢+媽媽的票錢+玲玲的票錢=一共要的錢”，這也是例題中兩種常規解法的思路依據。當這兩種解法學生都明白了，筆者追問學生：“如果反過來用減法可以嗎？”學生在討論與思考中得出：“看作三個成年人的錢-玲玲少用的錢=一共要的錢。”逆向思路也解出來了，學生感到很興奮，也感受到了成功的喜悅。多幾次對例題解法的逆向追問、逆向思考與逆向探索，學生的逆向思維意識就能得到培養。

三、在“逆練”中練習，培養逆向思維意識

在例題教授環節完成后，不少教師喜歡變換條件去訓練學生，不斷強化例子所傳遞出的解題方法，只要學生熟練了，就立刻停止采用這種方式訓練學生：一方面，學生很容易僵化，易養成按部就班的惰性思維——“唯書論”，學生的創新求異思維不易發展；另一方面，很多學生會練得很枯燥，不利其積極情感態度的形成。其實，還可以進行一些逆思維練習，打破學生對常用解法的慣性認識。常用的“逆”練習有兩種形式：一是逆著教材的格式進行練習。這就是一種最簡單的逆向思維練習，在低年級教學中可以經常使用。

例如，“20以內數的認識”一課。學生能熟練地從1數到20后，教師不能僅局限于此，還要求學生會從20倒著數到1，會填一些倒著數的數格練習。在教學“10以內的加法”后，教師不但要讓學生練“3+4=？”這樣正向形式的練習，還要讓他們練習“7=□+□”這種逆向形式的練習，能滿足學習層次不同的學生的學習需要。二是逆著教例的解題方法去練。例如，“乘數是兩位數的小數乘法”，例題的方法是被乘數先乘乘數的個位再乘十位（即從低位開始乘的方法）。練習時，當學生會用這種方法計算，且比較熟練后，教師說：“是不是一定要從乘數的低位開始乘起呢？我們能不能反過來從乘數的高位開始乘起呢？”學生的探究熱情高漲，經過嘗試，發現完全可以。為了印證這種方法的可行性，教師道出了市場上很多菜農不借助計算器，卻很快算出總價的奧秘。

這樣“逆”著練，不但豐富了解法，適應不同層次學生的發展需要，更重要的是能打破學生的常規思維，開拓求異思維，從而發展學生的逆向思維意識。

四、在“逆追”中歸納，培養逆向思維意識

知識自成體系，但它散落在各冊教材或各個課時中，學完一部分知識后，教師都要組織學生進行歸納，促使知識系統的形成，常用的方法是順著知識的推進過程進行歸納，這種方式有一個缺點：學生憑著知識學習先后順序的自然感覺去歸納，沒有真正去思考為什么這樣構網成絡，缺乏對知識之間內在邏輯聯系的思考。在教學時，筆者常逆著知識的進程進行歸納。

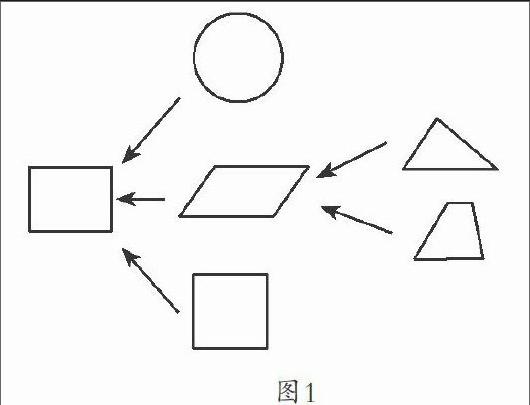
例如，在學習“圓面積計算”一課，小學階段平面圖形部分的認識也結束了。為構建知識系統，筆者進行了總結。總結時，筆者不是順著圖形的先后學習順序及內在聯系去歸類總結，而是從最后學的圓形逆過來去追尋知識系統，直接提問：“我們學了許多平面圖形，今天來構建知識樹，如果從剛學的圓逆推回去，你認為圓的上一層平面圖形是什么？為什么？”于是學生就從已學過的平面圖形（長方形、正方形、平行四邊形、三角形、梯形）中去尋找，通過分析它們之間的內在“機理”，發現圓可以轉化成長方形，得出圓的上一層知識點是長方形。針對在分析中學生知道了梯形和三角形不是圓的上一層知識點，筆者追問道：“既然梯形不是圓的上一層知識點，那么梯形的上一層知識點是什么呢？”學生構建出“梯形→平行四邊形”的知識聯結，接著放手讓學生運用逆推思維和平行思維去尋找各種平面圖形的關系，最終形成這樣的知識樹（如圖1），學生在追溯過程中，找到了小學階段的平面圖形知識的根是長方形，同時理清了各種圖形之間的邏輯關系，使這些散亂的知識，變成了一串有序、緊密聯系的知識鏈。教學中，多一些這種尋根溯源的逆向歸納總結，學生不但能深入分析知識間內在的邏輯關系，形成深刻的知識鏈，而且在逆向尋“根”中，培養了學生的逆向思維意識。

（作者單位：福建省長汀縣城關中區小學 責任編輯：王彬）endprint