徑向激勵作用下有限長雙層圓柱殼聲振傳遞特性研究

楊曉剛，林立，白振國，李兵

（1中國艦船研究院，北京100192；2中國船舶科學研究中心，江蘇無錫214082）

徑向激勵作用下有限長雙層圓柱殼聲振傳遞特性研究

楊曉剛1，林立1，白振國2，李兵1

（1中國艦船研究院，北京100192；2中國船舶科學研究中心，江蘇無錫214082）

文章利用Donnel殼體方程描述雙層圓柱殼振動，以附加阻抗的形式表示環肋、實肋板以及水介質等對殼體的力作用，結合內外殼振動位移模態展開形式，建立了雙層圓柱殼內外殼之間的聲振傳遞矩陣。同時開展了雙層圓柱殼外殼均方速度響應仿真分析，驗證了雙層圓柱殼內外殼振動響應之間存在固定的傳遞關系，不受激勵源特性影響，為雙層圓柱殼輻射噪聲預估提供了一定的理論指導。

聲振傳遞；傳遞矩陣；雙層圓柱殼

0 引言

機械噪聲是水下航行器低速工況下的主要噪聲源，因此機械設備激勵引起的結構振動和聲輻射問題一直備受關注。水下航行器在航行過程中，機械設備通過隔振系統激勵基座，并沿基座傳遞到內殼上，或者通過管路系統激起內殼振動；然后部分振動能量經雙層殼體之間的水介質以及實肋板等支撐結構傳遞到外殼體，并向外場輻射噪聲。

目前針對水下航行器輻射噪聲預報，中低頻段主要采用有限元法和邊界元法，中高頻段主要采用統計能量法，這些方法主要以設備激勵力或輸入功率為初始輸入參數，但是目前缺乏客觀合理的設備激勵力或其它有效的激勵輸入參數等[1]，難以由設備激勵或基座響應準確預報輻射噪聲。同時，由于外場水介質作用，外殼表面難以布置大量振動傳感器[2]直接由外殼振動數據預報輻射噪聲。因此基于振動能量傳遞過程，利用內殼振動數據預估外殼振動響應，進而預估輻射噪聲成為比較有效的途徑，雙層圓柱殼聲振傳遞特性研究對輻射噪聲預估具有重要的意義。

國內外學者針對雙層圓柱殼聲振傳遞特性開展了大量研究，主要是通過解析法和數值法建立雙層圓柱殼聲振耦合模型，獲取內外殼聲振傳遞關系。白振國[3]利用模態展開法，建立了有限長雙層加肋圓柱殼聲振耦合模型，詳細分析了實肋板、環肋以及激勵特性等參數對雙層殼間聲振耦合特性的影響；陳美霞等[4-6]利用Flügge殼體理論，把環肋、縱骨、托板或實肋板視為動反力作用在殼體上，建立了雙殼體結構—聲—流體耦合方程，對比了連接形式等對雙層圓柱殼聲振特性的影響；金廣文[2]基于頻響函數求逆法，建立了內外殼體之間的振動傳遞矩陣，該傳遞矩陣受激勵源、邊界條件等影響；文獻[7]利用有限元法和邊界元法建立了雙層殼體流固耦合數值模型，并對雙層圓柱殼的水下受激振動和聲輻射進行了數值分析。

考慮到實際水下航行器的復雜性，難以建立解析和數值簡化模型，同時存在計算量過大和精度不理想的問題。因此根據工程實際，可以利用模型或實際結構的振動和噪聲測試數據，回歸獲取內外殼體的聲振耦合傳遞關系，此技術途徑存在的一個關鍵性問題是首先要驗證內外殼振動傳遞和聲場耦合是否存在與激勵源無關的傳遞關系，這樣才能以此為基礎，針對不同激勵力工況，由內殼振動預估外殼振動，進一步預估輻射噪聲。為此，本文以有限長雙層圓柱殼為例，理論推導建立了內殼振動到外殼振動的聲振傳遞矩陣，并數值仿真分析了激勵源特性對內外殼聲振傳遞特性的影響。

1 雙層圓柱殼聲振傳遞理論

本文研究的模型為有限長雙層圓柱殼：內殼體表面環向分布周期性環肋；內外殼之間由實肋板連接并且充滿水介質；外殼外部為無限大理想水介質。雙層圓柱殼物理模型如圖1所示。且假設雙層圓柱殼兩端簡支，并有無限大圓柱形聲障板；殼間實肋板為聲透明，不影響殼間聲傳播。

雙層圓柱殼振動采用Donnel殼體理論描述。

圖1 有限長雙層圓柱殼模型Fig.1 Model of double finite length cylindrical shells

其中：ui、vi、wi分別為內外殼的軸向、周向和徑向位移；ai、hi、分別為內外殼半徑、厚度以及厚徑比；cp為殼體縱波聲速；E、μ分別為殼體材料楊氏模量和泊松比分別為環肋對內外殼作用力分別為殼間實肋板對內外殼作用力；分別為殼間以及外場水介質對內外殼的作用力為作用在圓柱殼上的激勵力。

僅考慮徑向對稱激勵，則雙層圓柱殼軸向、周向和徑向位移可表示為：

將方程式（2）代入到雙層圓柱殼振動方程（1）中，可獲得雙層圓柱殼振動矩陣方程，同時將環肋、實肋板等結構對內外殼體作用視為離散的反作用力，結合邊界條件，推導殼體附加阻抗的表達式，進而組裝形成雙層圓柱殼聲振耦合方程組（3）式。

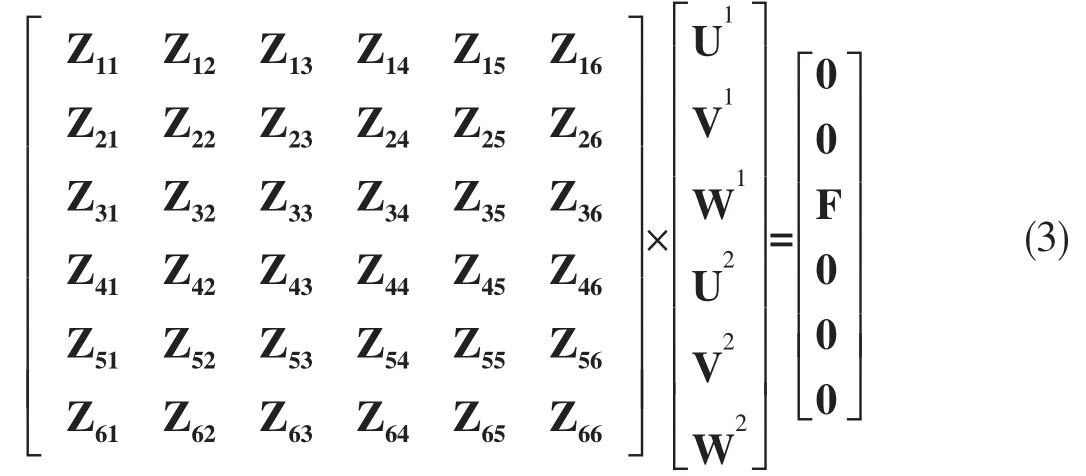
其中雙層圓柱殼模態阻抗矩陣中子矩陣元素Zij以及環肋、實肋板、水介質等的附加作用阻抗詳細求解過程參見文獻[3]，F為徑向模態作用力。

水下航行器上機械設備等產生的激勵力主要為徑向作用力，且殼體聲輻射也主要由徑向振動激發，因此本文僅考慮雙層圓柱殼內外殼體徑向聲振耦合特性，為了便于分析，移動（3）式模態阻抗矩陣中Z31行元素至Z51行元素之后，同時相應調整（3）式中模態分量矩陣和模態作用力矩陣中元素的位置，將內外殼體的軸向模態分量U1、U2和周向模態分量V1、V2組合為一個新變量M，得到雙層圓柱殼模態運動方程，如（4）式所示。

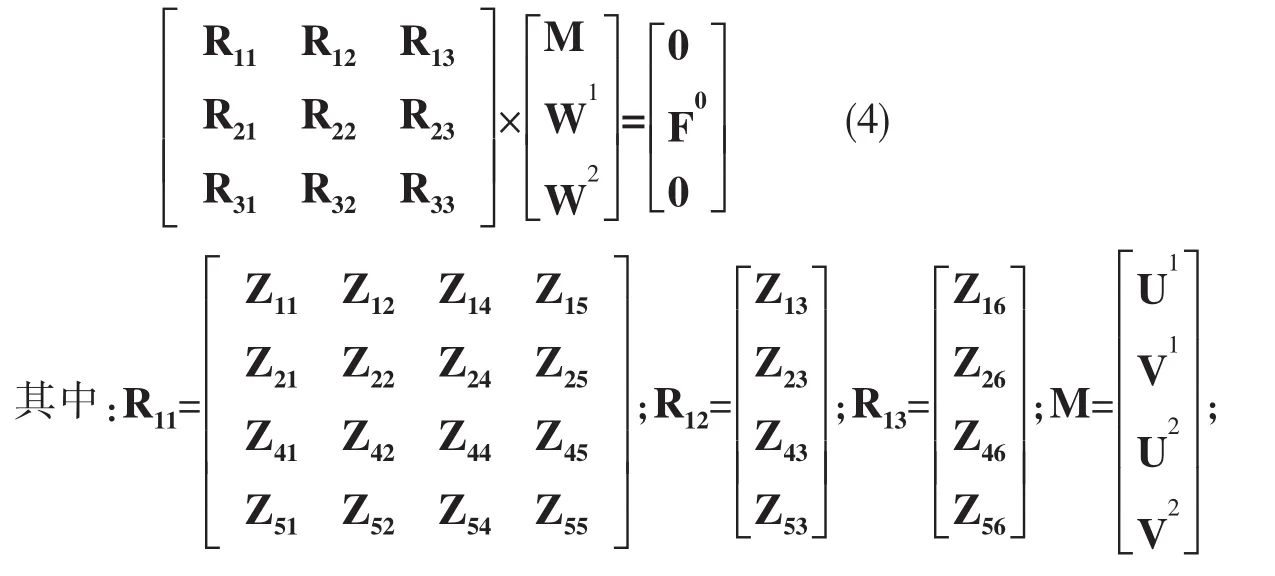
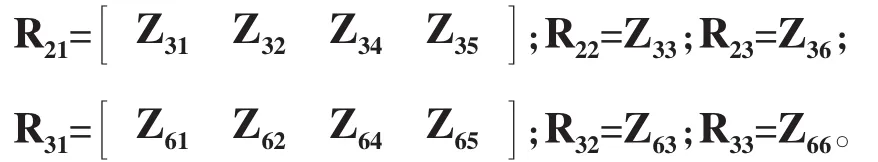
為了研究內殼和外殼徑向聲振傳遞特性，需要建立內殼的徑向位移模態分量W1和外殼的徑向位移模態分量W2之間關系，將方程組（4）分解，可得：

由（5）式可得：

進而將（6）式代入（2）式，利用內殼的徑向模態分量W1表示外殼的徑向振動位移w2，可得：

將（8）式代入（7）式中，可以獲得內外殼體聲振傳遞關系：

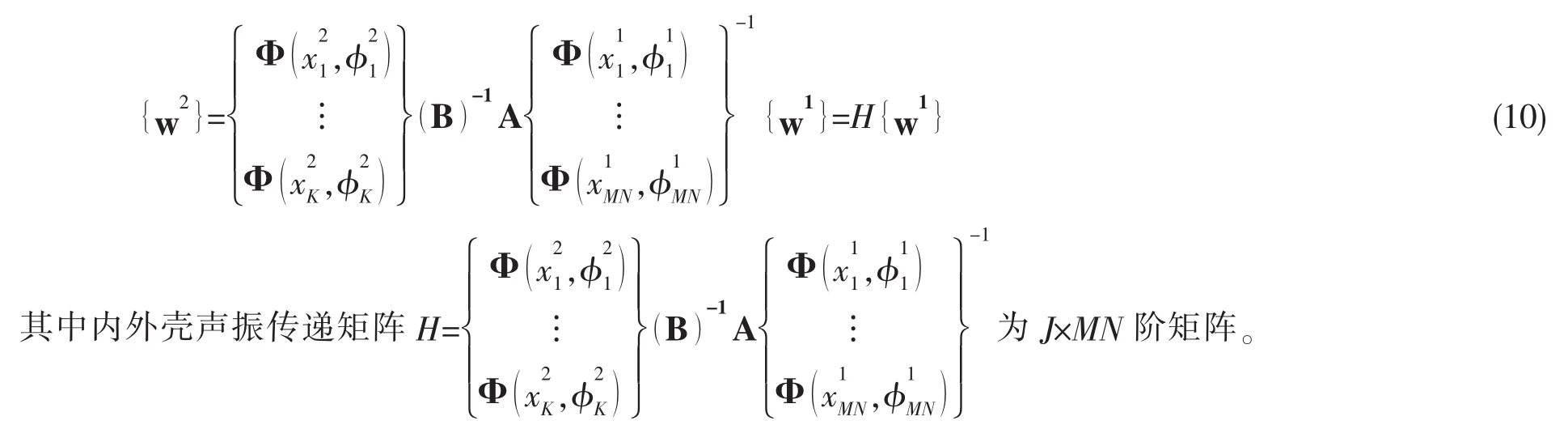
根據內外殼聲振傳遞矩陣表達式可知，聲振傳遞矩陣僅與雙層圓柱殼模態阻抗、內外殼振動測點位置及數量相關，與激勵源特性無關，而模態阻抗由雙層圓柱殼結構決定，即雙層圓柱殼結構和振動測點位置固定時，內外殼之間存在固定的聲振傳遞矩陣。后文對雙層圓柱殼內外殼振動響應進行了數值仿真，分別從激勵源數量、位置和形式三個方面研究激勵源特性對內外殼聲振傳遞關系影響，以驗證內外殼聲振傳遞關系與激勵源特性無關。

2 仿真計算和分析

本節選用的有限長雙層圓柱殼模型參數：內殼半徑a1=3.5 m，外殼半徑a2=4.3 m，內殼厚度h1=28 mm，外殼厚度h2=10 mm，殼體長度L=9.6 m，內殼上均布4個T型環肋，內外殼之間由3個實肋板連接，實肋板厚度5 mm，殼體材料為鋼，楊氏模量E=2.1×1011N/m2，泊松比μ=0.3，內外殼之間以及外殼外部充滿理想水介質。

經雙層圓柱殼聲振耦合理論收斂性驗證，周向波數N=41，軸向波數M=60時，雙層圓柱殼輻射噪聲有效計算頻段可達1-500 Hz。由雙層圓柱殼內外殼聲振傳遞矩陣理論推導過程可知，內殼應布置M×N個振動測點，因此本文內殼上周向均布41個測點，軸向均布60環測點，同時為有效反映外殼振動狀態，外殼軸向和周向各均布11個測點，從而建立雙層圓柱殼內外殼聲振傳遞矩陣。

本文根據（3）式可求解出雙層圓柱殼內外殼徑向振動位移模態分量，進而由（2）式可直接計算出內外殼振動響應；同時利用計算得到的內殼振動響應和內外殼聲振傳遞矩陣，由（13）式可間接求解外殼振動響應，分別對比激勵源數量、位置、形式發生變化時外殼均方速度響應間接求解和直接求解結果，分析激勵源特性對內外殼聲振傳遞關系的影響。振動速度級基準為：v0=1×10-6m/s。

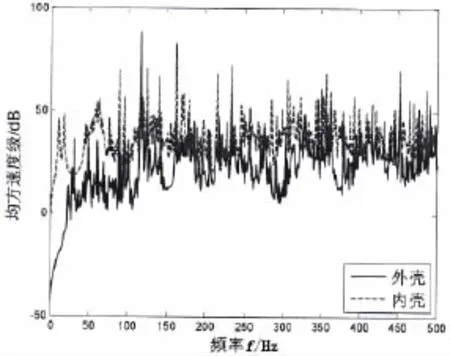
圖2 內外殼均方速度級Fig.2 Comparison of mean square velocity level both the inner and outer shell

2.1 激勵數量對雙層圓柱殼聲振傳遞關系影響

圖3和圖4分別給出了單位點激勵力作用下外殼均方速度響應和外殼測點1振動響應。激勵作用位置1：外殼測點1位置：xw1=4.7 m，φw1=0。圖5為雙層圓柱殼軸向均布10個、20個單位激勵作用下外殼均方速度響應。

圖3和圖4可知，單位激勵力作用下，外殼速度響應的直接求解結果和間接求解結果完全吻合，即利用內外殼聲振傳遞關系可準確預估點激勵作用下外殼響應。

由圖5可知，增加激勵源數量，雙層圓柱殼外殼均方速度響應變大，即雙層圓柱殼振動特性發生變化，但利用內殼振動響應和聲振傳遞矩陣間接求解的外殼振動響應與直接求解結果完全吻合，這表明雙層圓柱殼聲振傳遞關系不受激勵源數量影響。

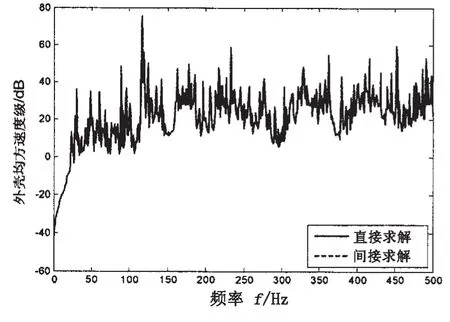
圖3 單位激勵作用下外殼均方速度級Fig.3 Mean square velocity level of the outer shell under unite force excitation

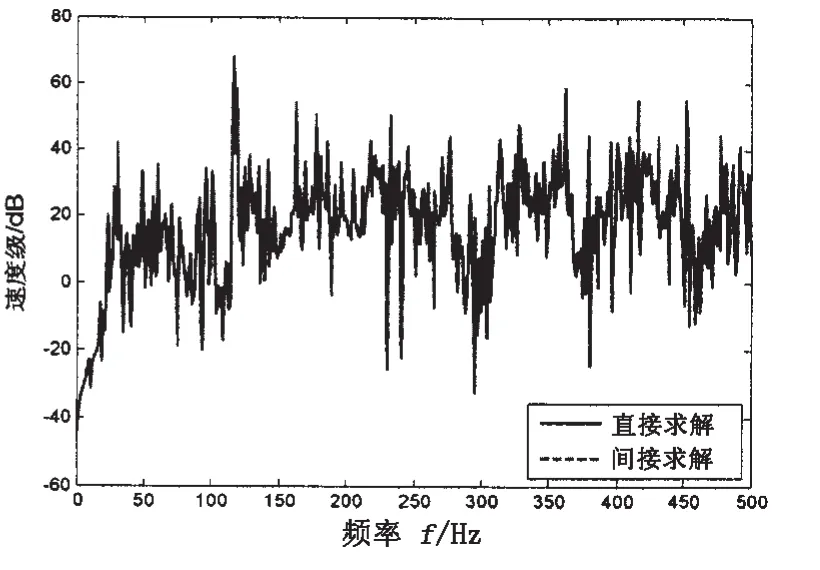
圖4 單位激勵作用下測點1速度級Fig.4 The velocity level of measured point 1 under unite force excitation

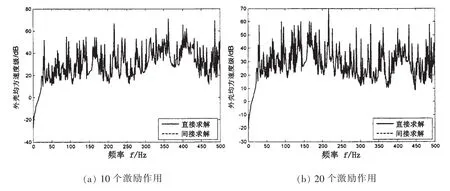
圖5 不同數量激勵作用下外殼均方速度級Fig.5 Mean square velocity level of the outer shell under different amount of force excitations

2.2 激勵位置對雙層圓柱殼聲振傳遞關系影響

圖6給出了點激勵作用于不同位置處外殼均方速度響應。激勵作用位置2：激勵位置3：兩激勵位置關于（2.1）中激勵作用位置1對稱。

由圖6可知，在1-500 Hz頻段內，利用文中直接求解方法獲得的外殼平均振動響應和利用雙層圓柱殼聲振傳遞矩陣間接獲得的外殼平均振動響應曲線完全吻合，這表明激勵源位置不會對雙層圓柱殼內外殼聲振傳遞關系產生影響。

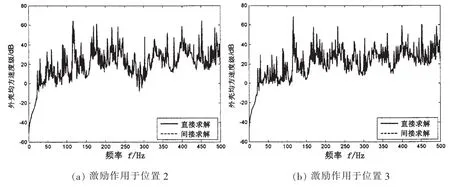
圖6 激勵作用于不同位置時外殼均方速度級Fig.6 Mean square velocity level of the outer shell under force excitation to different position

2.3激勵形式對雙層圓柱殼聲振傳遞關系影響

圖7為周向線激勵力、軸向線激勵力作用下外殼均方速度響應。軸向和周向線激勵力都以（2.1）中激勵作用位置1為中心，作用長度為2 m，各個力與單位點激勵力在積分意義上相等。

由圖7可知，將點激勵更換為線激勵，激勵源形式發生變化，但外殼平均速度響應的直接求解結果和間接求解結果仍完全吻合，即改變激勵力的形式，雙層圓柱殼內外殼之間依然存在固定的聲振傳遞關系。

圖8為長方形面激勵、環形面激勵作用下外殼均方速度響應。兩種形式面力都以為中心，長方形面激勵軸向長度為9.6 m，周向寬度為0.2 m；環形面激勵寬度為0.2 m，兩個面力與單位點激勵力在積分意義上相等。

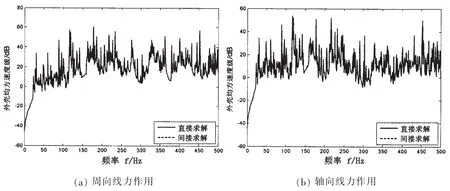
圖7 線力作用下外殼均方速度級Fig.7 Mean square velocity level of the outer shell under different line force excitation

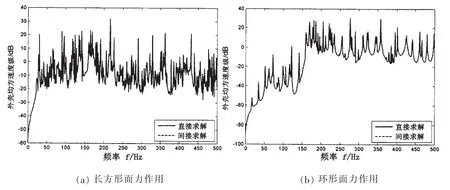
圖8 面力作用下外殼均方速度級Fig.8 Mean square velocity level of the outer shell under different surface force excitation

由圖8可知，兩種不同形式面激勵作用下，外殼振動響應發生變化，尤其是200 Hz以下中低頻段，環形面力作用下，外殼振動響應小于長方形面力作用下外殼振動響應，但是利用內殼響應和內外殼聲振傳遞矩陣依然能夠準確預估外殼響應，進一步表明文中獲得的聲振傳遞矩陣與激勵源形式無關。

2.4 內殼測點位置偏差對外殼響應預估的影響

考慮到實際水下航行器結構復雜，難以獲得內殼振動傳感器的精確位置，從而導致實際傳感器布置位置與聲振傳遞矩陣求解過程使用的內殼測點位置有一定的偏差。因此，本節在前文研究基礎上，在一定范圍內改變內殼測點位置，利用單位激勵下，測點位置變化后內殼振動數據和前文建立的聲振傳遞矩陣預估外殼振動響應，并與利用測點位置未發生變化時內殼振動數據預估的外殼響應結果對比，從而分析內殼測點位置偏差對外殼響應預估精度的影響。圖9為單位激勵下，內殼測點位置在軸向、周向以及在軸向和周向都發生偏差前后利用內外殼聲振傳遞矩陣間接求解的外殼均方速度響應對比曲線，測點位置軸向和周向的偏差范圍為5 cm。

由圖9可知，內殼測點位置在軸向發生偏差時，40 Hz以下，150 Hz以上頻段內殼測點位置發生偏差前后外殼響應預估結果基本一致，40-150 Hz頻段內內殼測點位置發生偏差前后外殼響應預估結果趨勢相同，幅值差別比較大；內殼測點位置在周向發生偏差時，利用準確的內殼測點位置和利用發生偏差的內殼位置處振動數據預估的外殼響應曲線基本吻合，表明外殼響應預估結果準確性主要受軸向位置偏差影響，這是由于雙層圓柱殼實肋板和環肋周向連續分布，軸向離散分布導致的。

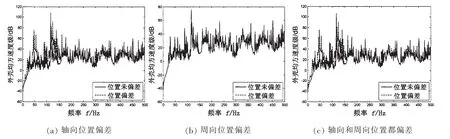
圖9 內殼測點位置偏差時外殼均方速度級Fig.9 Mean square velocity level of the outer shell during measuring point position of the inner shell changed (a)Position deviation in circumference;(b)Position deviation in axis;(c)Position deviation both in axis and circumference

3 結論

本文對有限長雙層圓柱殼內外殼之間聲振傳遞關系進行了研究，基于聲振耦合機理，理論推導出內外殼之間的聲振傳遞矩陣僅與雙層圓柱殼結構、測點位置和數量相關，與激勵源特性無關。雙層圓柱殼外殼響應仿真計算證實激勵源數量、位置、形式等特性的改變不會對內外殼振動傳遞特性產生響應，仿真結果同時表明利用內外殼聲振傳遞關系預估外殼振動響應時，內殼測點軸向位置偏差影響大于周向位置偏差影響。該結論可為后續利用水下航行器實測振動數據，回歸內外殼體聲振耦合傳遞關系，實現基于內殼振動響應預估外殼振動響應提供理論支撐。

[1]趙智偉.有限長圓柱殼聲與振動的快速預報方法研究[D].哈爾濱:哈爾濱工程大學,2007. Zhao Zhiwei.Research on fast predicting method of sound and vibration from a finite cylindrical shell[D].Harbin:Harbin Engineering University,2007.(in Chinese)

[2]金廣文,何琳,姜榮俊.基于速度場重構的雙層圓柱殼振動傳遞特性試驗研究[J].振動與沖擊,2007,10(26):180-183. Jin Guangwen,He Lin,Jiang Rongjun.Vibration of transmissibility of a ribbed cylindrical double-shell based on reconstructing velocity field[J].Journal of Vibration and Shock,2007,26(10):180-183.(in Chinese)

[3]白振國.雙層圓柱殼舷間聲振耦合特性及控制技術[D].無錫:中國船舶科學研究中心,2104. Bai Zhenguo.Vibration and sound coupling behavior and control method of double-layer cylindrical shells[D].Wuxi:China Ship Scientific Research Center,2014.(in Chinese)

[4]陳美霞,金家坤,彭旭等.內、外殼對水下雙層圓柱殼聲振性能影響分析[J].船舶力學,2009,4(13):628-634.Chen Meixia,Jin Jiakun,Peng Xu,et al.Influence by the inner shell and the outer shell on sound-vibration characteristics from double cylindrical shells in water[J].Journal of Ship Mechanics,2009,13(4):628-634.(in Chinese)

[5]高菊,陳美霞,陳清坤等.不同流場中雙層圓柱殼層間聲振傳遞特性研究[J].中國艦船研究,2010,5(10):34-39. Gao Ju,Chen Meixia,Chen Qingkun,et al.Sound and vibration transmission characteristics between inner and outer double cylindrical shells in different flow fields[J].Chinese Journal of Ship Research,2010,5(10):34-39.(in Chinese)

[6]夏齊強,陳志堅.殼間聲橋剛度對雙層圓柱殼聲振耦合特性的影響[J].海軍工程大學學報,2013,1(25):90-95. Xia Qiqiang,Chen Zhijian.Effect of stiffness of sound bridge between shells on vibro-acoustic coupling characteri-sticcs of double cylindrical shell[J].Journal of Naval University of Engineering,2013,1(25):90-95.(in Chinese)

[7]商德江,何祚鏞.加肋雙層圓柱殼振動聲輻射數值計算分析[J].聲學學報,2001,26(3):193-201. Shang Dejiang,He Zuoyong.The numerical analysis of sound and vibration from a ring-stiffened cylindrical double shell by FEM and BEM[J].Chinese Journal of Acoustics,2001,6(3):193-201.(in Chinese)

Sound and vibration transmission characteristic of finite length double cylindrical shells under radial excitation

YANG Xiao-gang1,LIN Li1,BAI Zhen-guo2,LI Bing1
(1.China Ship Research Development Academy,Beijing 100192,China;2.China Ship Scientific Research Center, Wuxi 214082,China)

The Donnell equation of thin shell was applied to describe double cylindrical shells motion.The effect of the rings,annular pales and the fluid was treated as forces and moments on shells,which were presented in terms of the additional impedance.By using the mode expanding expression of shell’s displacement,the sound and vibration transfer matrix between the inner and outer shell was constituted.The numerical analysis of mean square velocity of the outer shell was carried out.The result verified that the transfer matrix of the inner and outer shell was fixed,which was not influenced by excitation property.It offers the theoretical basis to predict the noise of double cylindrical shells.

sound and vibration transmission;transfer matrix;double cylindrical shell

TB532

A

10.3969/j.issn.1007-7294.2015.05.015

1007-7294（2015）05-0600-09

2015-03-05

楊曉剛（1989-），男，碩士研究生，E-mail：yxg2008300@126.com；

林立（1965-），女，研究員。