基于Copula理論和非參數(shù)極值估計在上下游水位的相關(guān)性分析應(yīng)用

趙凱鴿，袁永生，吳清嬌

(河海大學(xué)理學(xué)院，江蘇南京210098)

自從Sklar教授于1959年提出Copula函數(shù)的概念以來，經(jīng)過諸多學(xué)者的深入研究，形成了Copula函數(shù)的基本理論，并且在各個領(lǐng)域得到了廣泛應(yīng)用，取得了豐富的研究成果。Copula不僅將經(jīng)典統(tǒng)計學(xué)中的線性相關(guān)系數(shù)及其他相關(guān)系數(shù)與Copula函數(shù)聯(lián)系起來，推導(dǎo)出Copula函數(shù)與相關(guān)系數(shù)的關(guān)系式，并且能有效地解決一些非線性、非對稱的復(fù)雜相關(guān)性問題。Copula函數(shù)理論的核心是Sklar定理，其重要意義在于將聯(lián)合分布函數(shù)與其邊緣分布函數(shù)聯(lián)系起來，并提供了一種由一元邊緣分布構(gòu)造多元聯(lián)合分布函數(shù)的途徑和方法，其推論給出了利用連續(xù)分布函數(shù)的偽逆函數(shù)和聯(lián)合分布函數(shù)求出其相應(yīng)Copula函數(shù)的方法。Copula理論是一種定性與定量分析相結(jié)合的統(tǒng)計分析方法。

由Copula導(dǎo)出的相關(guān)性度量不僅可以描述變量間的非線性、非對稱相關(guān)關(guān)系，而且還可以刻畫尾部的相關(guān)性。把Copula與時變相結(jié)合，構(gòu)建了t-Copula模型，這一模型將Copula中的參數(shù)看成時間的某個確定函數(shù)來進(jìn)行建模，這樣將會減小模型假定錯誤所帶來的偏差。由于相關(guān)結(jié)構(gòu)具有相當(dāng)?shù)牟淮_定性和復(fù)雜性，Copula參數(shù)的時變結(jié)構(gòu)根本就是未知的，很多文獻(xiàn)采用半?yún)?shù)模型和非參數(shù)模型，更實用、更有效、更有意義。

事實上，很多模型的邊際分布是無法準(zhǔn)確定位的，因而傳統(tǒng)的參數(shù)估計存在一定的局限性。由于非參數(shù)估計是不需要事先知道模型的邊際分布，基于此，文中運用非參數(shù)技術(shù)來估計Copula函數(shù)中的參數(shù)，從而克服了傳統(tǒng)參數(shù)估計的不足。

在國外，F(xiàn)ermaniam［1］認(rèn)為高維數(shù)據(jù)進(jìn)行Rosenblatt變換比較困難，直接利用基于樣本數(shù)據(jù)的多變量核密度估計的密度函數(shù)與均勻密度函數(shù)相比較;Werker［2］利用秩相關(guān)函數(shù)τ的演化方程確立的時變Copula模型來研究波動溢出的問題;Genest［3］利用數(shù)據(jù)的概率積分變換來估計其相應(yīng)的密度模型，從而確定最優(yōu)的Copula函數(shù);Gordon和Johan對任意維下的極值Copula進(jìn)行非參數(shù)估計;Gudendorf G，Segers J［4］從理論上研究了任意維數(shù)的極值Copula函數(shù)的非參數(shù)估計。

在國內(nèi)，學(xué)者張堯庭［5］從理論上探討了Copula在金融上應(yīng)用的可行性;韋艷華、張世英［6］等用Copula-ARCh模型研究了上海證券市場中幾個板塊間的相關(guān)性;史道濟(jì)，張明恒［7］等也應(yīng)用Copula函數(shù)對金融市場的相關(guān)性作過一些探討;趙麗琴、籍艷麗［8］采用對邊際分布不作具體假設(shè)的非參數(shù)核密度估計Archimedean Copula的參數(shù)，并用實際說明其方法的有效性。

文中對現(xiàn)有的非參數(shù)估計量進(jìn)行改進(jìn)，克服了現(xiàn)有估計量的譜測度H的限制，并引進(jìn)新的非參數(shù)極值估計Z—L方法，以涇流從1975年到1996年上游和下游在不同時間的水位、流量和含沙為例，給出非參數(shù)估計的具體實現(xiàn)過程。

1 Copula理論簡介

Copula理論是由Sklar在1959年提出的。Sklar指出，可以將任意一個n維聯(lián)合累積分布函數(shù)分解為n個邊緣累積分布函數(shù)和一個Copula函數(shù)，其中邊緣分布函數(shù)描述的是變量的分布，Copula函數(shù)描述的是變量之間的相關(guān)性。也就是說，Copula函數(shù)實際上是一類將變量聯(lián)合累積分布函數(shù)同變量邊緣分布函數(shù)連接起來的紐帶函數(shù)，因此也有人稱其為“連接函數(shù)”。

1.1 Copu la函數(shù)的定義及Sk lar定理

定義1 n維Copula函數(shù)［9］(或稱為n－Copula)是一個函數(shù)C，具有如下性質(zhì):

1)定義域為 In，即［0，1］n;

2)對于任意 t=(t1，t2，…，tn)∈［0，1］n，若至少有一個tk=0，則C(t)=0;

3)C有零基面(grounded)，且是n維遞增的，即對于定義域中的任意真子集

B= ［a1，b1］× ［a2，b2］× …［an，bn］有

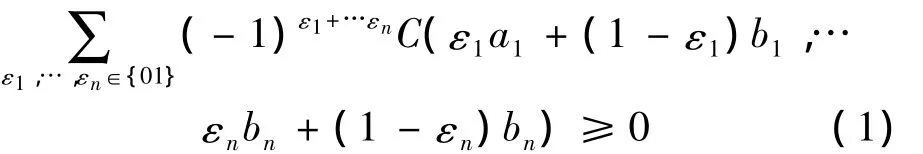
4)對于任意u∈［0，1］，C的邊緣函數(shù)Ck滿足

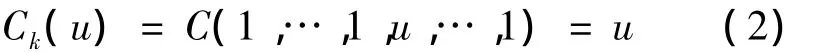
定理2(Sklar定理)Sklar定理［10］是 Copula函數(shù)理論的核心，也是基礎(chǔ)，在統(tǒng)計學(xué)中的應(yīng)用最為廣泛，其闡明了多元分布函數(shù)與其邊緣分布函數(shù)的關(guān)系。

令F是d維聯(lián)合分布函數(shù)，其邊緣分布F1，…，F(xiàn)d，一定存在一個 d－Copula函數(shù)C，對于任意向量x=(x1，…，xd)∈ Rd，則有

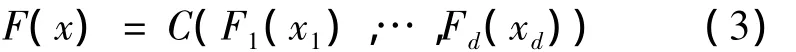
如果F1，…，F(xiàn)d都是連續(xù)的，則C是唯一的;否則C在Ran F1×…×Ran Fd上是唯一的。相反，如果C是一個d－Copula且F1，…，F(xiàn)d是邊緣分布函數(shù)，則由式(3)確定的函數(shù)是邊緣分布為F1，…，F(xiàn)d的d維聯(lián)合分布函數(shù)。

對于有連續(xù)的邊緣分布情況，對于所有的u∈［0，1］d，均有

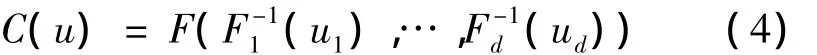
1.2 隨機(jī)變量間的相關(guān)性度量

任何變量之間如果不是相互獨立的，那么一定會存在一定的相關(guān)關(guān)系。幾種常用的刻畫多個隨機(jī)變量之間的相關(guān)性度量，有線性相關(guān)系數(shù)、Kendall秩相依系數(shù)、Spearman秩相依系數(shù)、尾部相關(guān)系數(shù)等，其中Kendall秩相依系數(shù)和Spearman秩相依系數(shù)是刻畫一致性的，而尾部相關(guān)系數(shù)是一個極值理論的測度，用來表示當(dāng)一個觀測變量的實現(xiàn)值為極值時，另一個變量也出現(xiàn)極值的概率。

相關(guān)性一直是人們關(guān)注的一個焦點問題。Nelsen指出，若對變量作單調(diào)增的變換，相應(yīng)的Copula函數(shù)不變，因而由Copula函數(shù)導(dǎo)出的一致性和相關(guān)性測度的值也不會改變。

1.2.1 線性相關(guān)系數(shù)(Linear Correlation)(x，

y)T為一個具有非零有限方差的隨機(jī)向量，則基于兩個隨機(jī)向量(x，y)T的線性相關(guān)系數(shù)被定義為

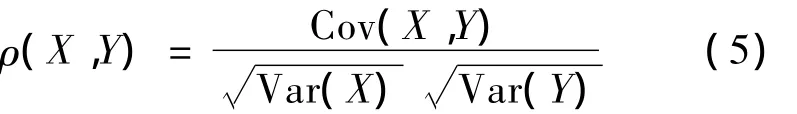
如果兩個隨機(jī)變量是獨立的，它們的線性相關(guān)系數(shù)ρ(x，y)=0;但是反過來卻并不成立。如果 |ρ(x，y)|=1，那么兩個隨機(jī)變量完全相關(guān)。在嚴(yán)格的單調(diào)遞增線性變換中，線性相關(guān)系數(shù)是不變的;但在嚴(yán)格的單調(diào)遞增的非線性變換中，相關(guān)系數(shù)卻是改變的。

1.2.2 Kendall秩相依系數(shù)

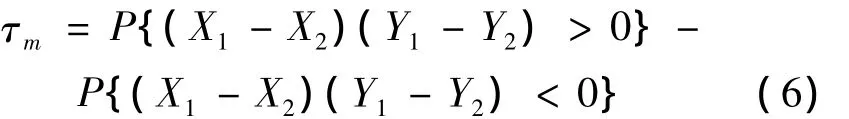
因此，Kendall秩相依系數(shù) τm［3］可以用來反應(yīng)隨機(jī)向量變化一致性的程度。特別地，當(dāng)τm=1、τm=－1和τm=0時，分布表示X和Y變化完全一致正相關(guān)、完全一致負(fù)相關(guān)和不能確定是否相關(guān)。

1.2.3 Spearman 秩相依系數(shù)

1.2.4 尾部相關(guān)系數(shù)

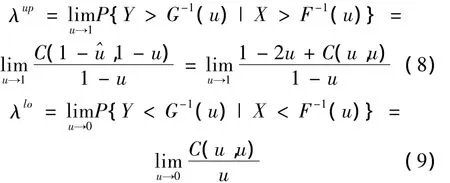
其中

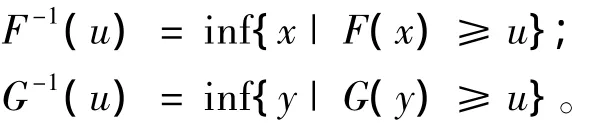
若尾部相關(guān)系數(shù)［6］λup或 λlo∈ (0，1］，則隨機(jī)變量X，Y上尾或下尾相關(guān);若λup或λlo=0，則隨機(jī)變量X，Y上尾或下尾漸進(jìn)獨立。

在實際生活中，數(shù)據(jù)多呈現(xiàn)出尖峰后尾性，對尾部相關(guān)關(guān)系的分析是掌握波動變化規(guī)律以及有效控制風(fēng)險的一個關(guān)鍵問題。而基于Copula函數(shù)的尾部相關(guān)系數(shù)包含了尾部相關(guān)的全部信息，就可以更全面、更深入地描述變量之間的相關(guān)關(guān)系。

1.3 極值Copula及其改進(jìn)

在實踐生活中，與極值分布函數(shù)［11］相對應(yīng)的是重要的極值Copula函數(shù)簇，而對于樣本最大值的廣義極值分布的邊緣

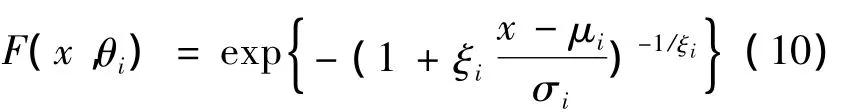
這里

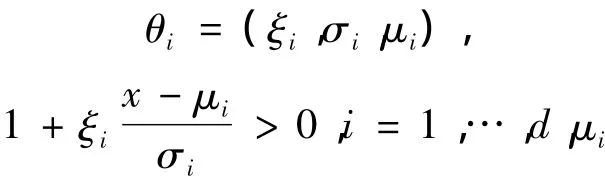
是一個位置參數(shù)，σi＞0是一個尺度參數(shù)，ξi∈R是一個形狀參數(shù)，它是極值指標(biāo)。

假定 Sij= － ln Fj(xij)，1≤i≤n，1≤j≤ d，并且是標(biāo)準(zhǔn)的指數(shù)自由變量對于 ω ∈ Δd－1，有

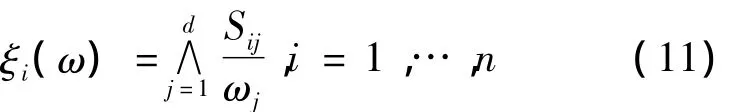
冪型方程:g(x)=xa，a ＞ 0，有

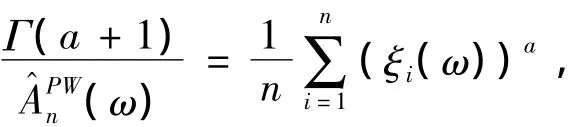
當(dāng)a=1時剛好是基本的Pickands型估計量。

對數(shù)方程:g(x)=ln x，有

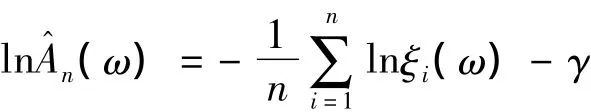
它剛好是CFG估計量。

上面兩個方程滿足頂點約束:A(ei)=1，…，d

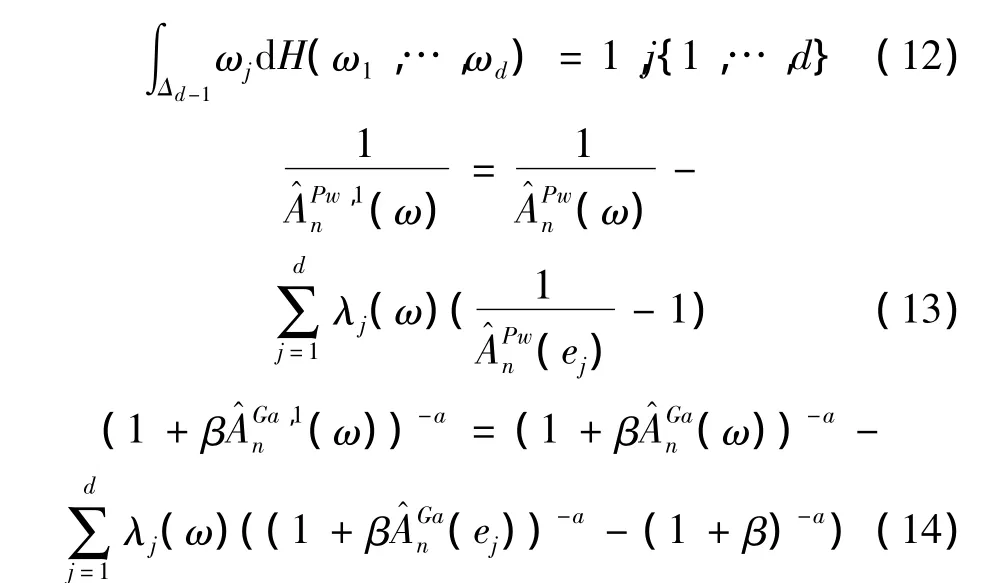
其中λj(ω):Δd－1→R上驗證λj(ek)= δjk，k=1，…，d是連續(xù)函數(shù)(δjk是克羅內(nèi)克δ方程)。所以有

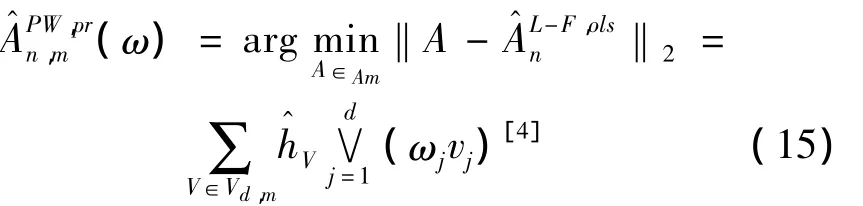
2 非參數(shù)核密度估計簡介

由于上下游水位高低分布出現(xiàn)的“尖峰”、“厚尾”現(xiàn)象，很多情況下不滿足正態(tài)分布。有文獻(xiàn)采用t－GARCH來描述，還有文獻(xiàn)采用經(jīng)驗分布來表述。這些方法都有合理的一面，但也有其不合理的一面。比如說，t－GARCH假設(shè)本身就是一種局限，而經(jīng)驗分布一般不連續(xù)，光滑性不夠，用來表述上下游水位高低的分布所產(chǎn)生的誤差較大，介于這些不利因素，現(xiàn)應(yīng)用非參數(shù)核密度估計技術(shù)來處理上下游水位的邊緣分布。

下面的結(jié)論仍然成立。

2.1 非參數(shù)核密度估計的定義及基本統(tǒng)計性質(zhì)

設(shè)K(·)為R1上一個給定的概率密度函數(shù)，hn＞0是一個與有關(guān)的常數(shù)，滿足當(dāng)n→∞，hn→0，則

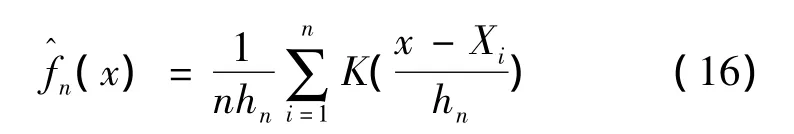
為f(x)的一個核估計，其中K(·)稱為核函數(shù)，hn為窗寬或光滑參數(shù)。

定理3 若(rA，rB)在點分布函數(shù)值的估計分別為

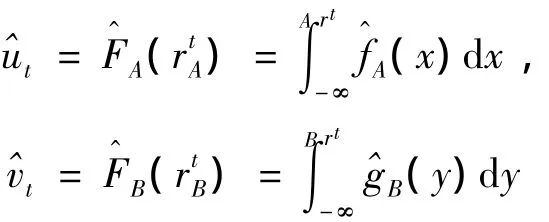
則當(dāng)核函數(shù)選取為正態(tài)核，上面兩式可以表示為

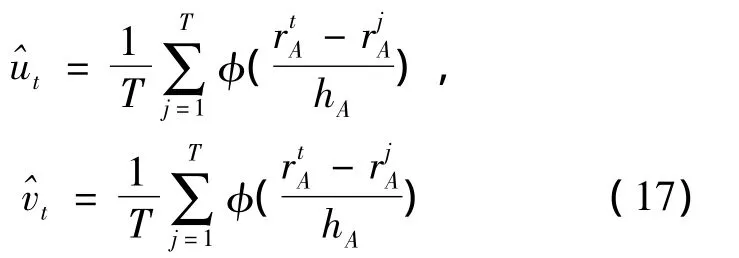
在進(jìn)行非參數(shù)核密度估計時，要解決的問題是如何選擇恰當(dāng)?shù)暮撕瘮?shù)及如何確定最優(yōu)的光滑參數(shù)。

2.2 核函數(shù)的選擇

核函數(shù)的選擇［13］可以有很多種，但是在一般情況下，核函數(shù)的選擇往往取決于根據(jù)距離分配各個樣本點對密度貢獻(xiàn)的不同。通常選擇什么樣的核函數(shù)并不是密度估計中最關(guān)鍵的因素，因為選用的任何核函數(shù)都能保證密度估計具有穩(wěn)定相合性。最重要的是光滑參數(shù)對估計分布的光滑程度影響很大，所以選擇什么樣的光滑參數(shù)是很重要的。

2.3 光滑參數(shù)的選取

由式(17)可知，核密度估計的應(yīng)用需要決定光滑參數(shù)hn，而分布密度函數(shù)是連續(xù)的，所以由的均方誤差(MISE)，即MISE的最小來確定hn。由極值定理，解

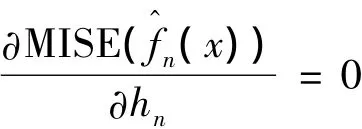
可得到hn的一個最使?jié)M意的解:

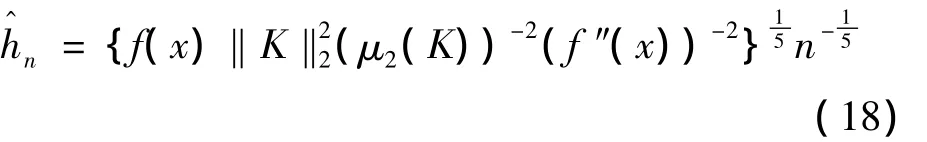
其中

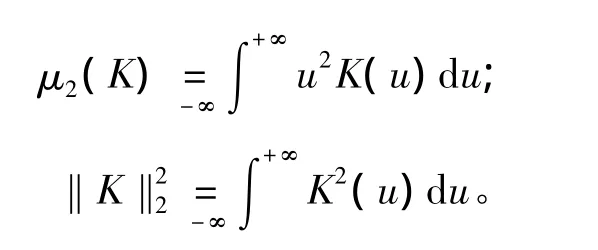
通常使用經(jīng)驗法則決定光滑參數(shù)，假設(shè)f(x)為正態(tài)概率密度N(0，σ2)，若核函數(shù)選取為正態(tài)核，則有

3 時變Copula模型的非參數(shù)極值估Z－L計算法

設(shè)有時間序列{(Xi，Yi)，t=1，2，…，T}，單變量隨機(jī)時間序列{Xi}和{Yi}都是平穩(wěn)的，現(xiàn)對{Xi}和{Yi}之間的聯(lián)合分布或相關(guān)結(jié)構(gòu)進(jìn)行建模，根據(jù)時變Copula模型的非參數(shù)估計思路，得出算法:

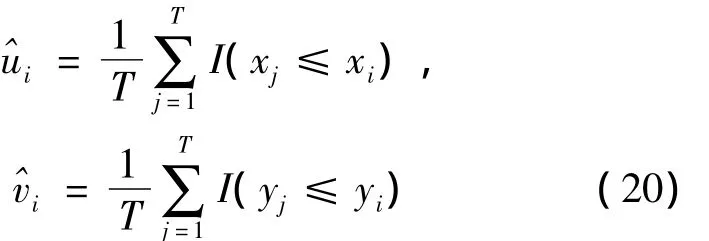
其中I(·)是示性函數(shù)。

其次，確定最佳光滑參數(shù)［14］，也就是給定光滑參數(shù)的可能取值集合，比如{h1，h2，…，hm};然后對光滑參數(shù)的每一個可能取值 hi，i=1，2，…，m，在偽樣本觀測條件下根據(jù)下式:

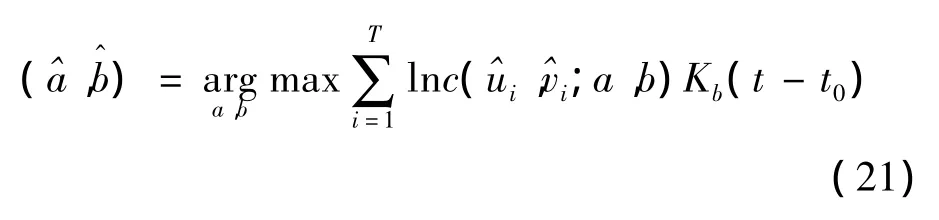
其中核函數(shù)選取

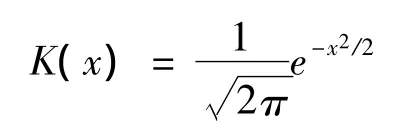
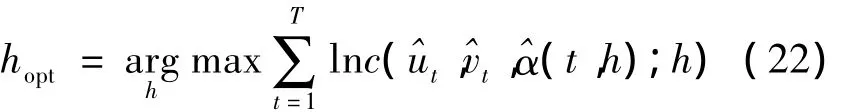
最后，時變Copula模型的非參數(shù)極值Z－L估計:

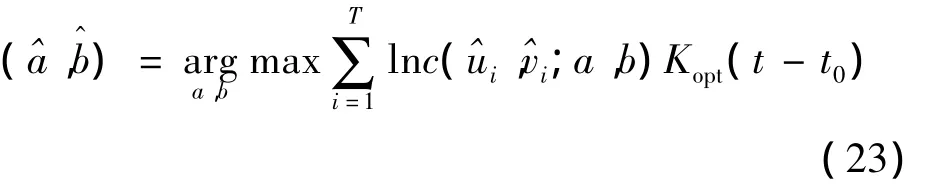
由式(23)就可以得到時變Copula模型的時間點t0的參數(shù)估計量(t0)=，再將此過程對每一個時間點進(jìn)行循環(huán)，就得到時變Copula模型參數(shù)估計量的時變軌跡。

4 徑流上下游水位的相關(guān)性

文中數(shù)據(jù)包括1975年至1996年夾河灘水位和高村水位，共計497個調(diào)查數(shù)據(jù)。首先用核方法來估計密度函數(shù)，核估計主要是由核密度函數(shù)和窗寬構(gòu)成。水位的變化率定義為:Xt=10(ln Pt－ lnt－1)，再選取高斯核函數(shù)

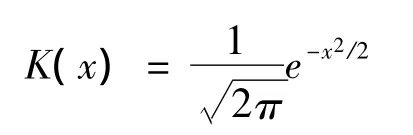
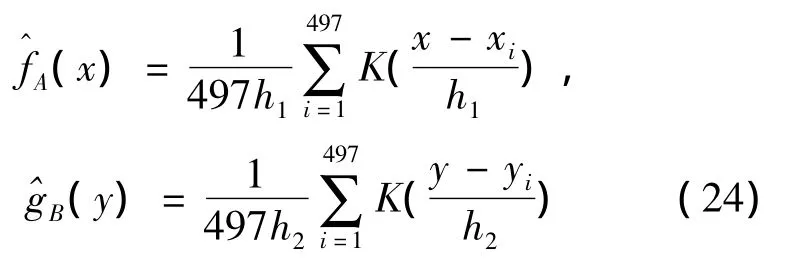
從圖1a，b可以看出，整個分布略顯左偏，表現(xiàn)出一定的間峰程度。夾河灘和高村的水位變化具有很強(qiáng)的厚尾性，且兩者間的變化存在一定的相關(guān)性，這和實際生活中的情況是一致的。下面觀察水位變化率序列的統(tǒng)計特征，其結(jié)果如表1所示。

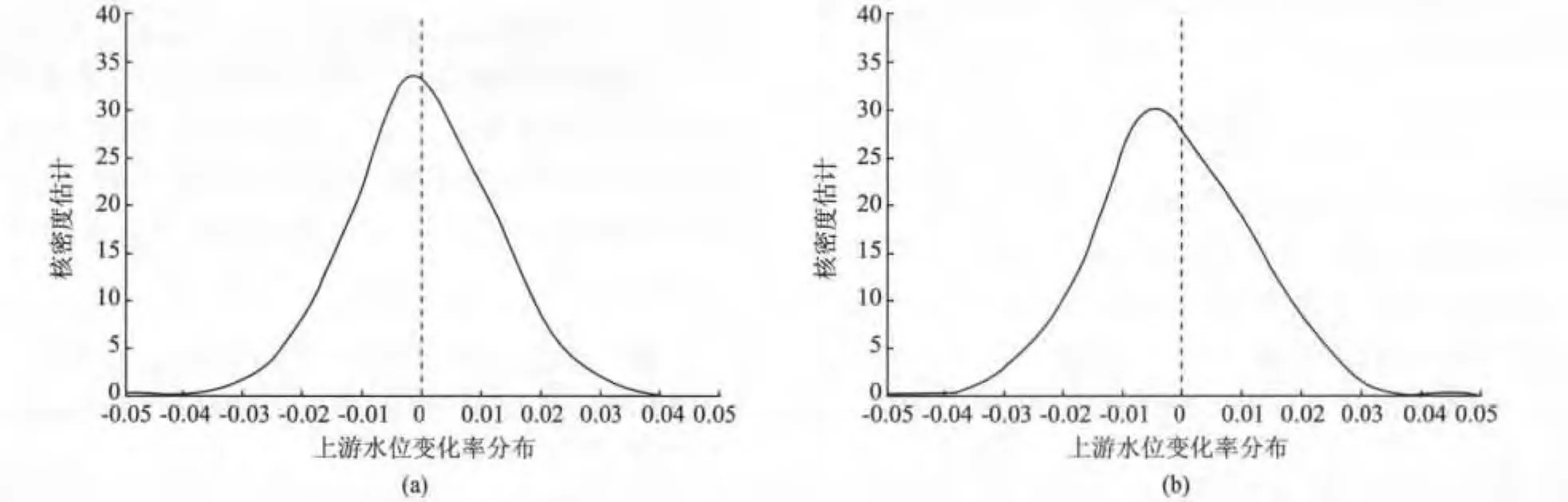
圖1 夾河灘和高村水位的邊際密度的核估計Fig.1 Nuclear estimate of the C lip quay’s and the High village’smarginal density

表1 上游、下游水位序列的基本統(tǒng)計Tab.1 Basic statistics of upstream and downstream’s water level sequences

由表1數(shù)據(jù)可以知道，上游和下游水位的均值和標(biāo)準(zhǔn)差都大于0，高村的峰度比較大，這即是經(jīng)常說的尖峰厚尾特征。負(fù)的偏度表明在整個調(diào)查期間，水位下降的天數(shù)少于上升的天數(shù)，每天上升的平均幅度高于每天下降的幅度。高的峰度表明水位以更大的概率出現(xiàn)在各自的均值附近。

圖2a，b分別給出上游夾河灘和下游高村的水位變化率的時間序列。可以看出，它們之間的波動有一定的相似性，這說明上游、下游水位的變化有一定的聯(lián)系。

還求得相應(yīng)的相關(guān)系數(shù)如下:Linear Correlation 0.735 36;Kendallτm0.914 83;Spearman ρk0.907 35;尾部相關(guān)系數(shù)0.886 21。數(shù)據(jù)說明上游夾河灘和下游高村的水位存在著較強(qiáng)的相關(guān)性，且ρk和τm比經(jīng)典的相關(guān)系數(shù)大，可見運用非參數(shù)核密度估計得到的Copula函數(shù)參數(shù)值是非常準(zhǔn)確的。

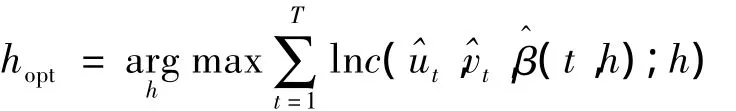
通過公式計算得到夾河灘、高村水位樣本的Kendalls秩相關(guān)系數(shù)，其值非常接近1，說明夾河灘和高村的水位具有極高的正相關(guān)性，與實際情況相符。同時也說明文中所估計的Copula是合理的，非參數(shù)極值估計Z－L算法在Copula函數(shù)的估計問題上是可行的。

表2 參數(shù)估計Tab.2 Parameter estimation

因此，非參數(shù)估計Copula密度函數(shù)在其度量模型相關(guān)方面是有意義的，并且在研究實際問題時，利用非參數(shù)估計相依模型間的聯(lián)系是很有效的，它也能夠避免由于失當(dāng)?shù)哪Ｐ突騾?shù)的選擇所產(chǎn)生的誤差。

致謝:東南大學(xué)數(shù)學(xué)系林金官教授所作關(guān)于《鏈接函數(shù)的非參數(shù)極值估計》的報告，對本文幫助很大，僅此致謝!

［1］Jean-David Fermanian J.Goodness-of-fit tests for Copulas［J］.Journal of Multivariate Analysis，2005，95(1):119-152.

［2］Rob W J，van den Goorbergh，Christian Genest，et al.Bivariate option pricing using dynamic copula models［J］.Insurance:Mathematicsand Economics，2005，37:101-114.

［3］Genest C J，Quessy F，Remillard B.Goodness-of-fit procedures for copulamodels based on the probability integral transform［J］.Scandinavian Journal of Statistics，2006，33(2):337-366.

［4］Gudendorf G，Segers J.Nonparametric estimation of an extreme-value copula in arbitrary dimensions［J］.Journal of Multivariate Analysis，2011，102(1):37-47.

［5］張堯庭.連接函數(shù)(Copula)技術(shù)與金融風(fēng)險分析［J］.統(tǒng)計研究，2002(4):48-51.ZHANG Tingyao.Copula technique and risk analysis［J］.Journal of Northwest Statistical Research，2002(4):48-51.(in Chinese)

［6］韋艷華，張世英，孟利峰.Copula理論在金融上的應(yīng)用［J］.西北農(nóng)林科技大學(xué)學(xué)報:社會科學(xué)版，2003，3(5):97-101.WEIYanhua，ZHANG Shiying，MENG Lifeng.The application of Copula in the financial［J］.Journal of Northwest Sci-Tech University of Agriculture and Forestry:Social Science Edition，2003，3(5):97-101.(in Chinese)

［7］張明恒.多金融資產(chǎn)風(fēng)險價值的Copula計量方法研究［J］.數(shù)量經(jīng)濟(jì)技術(shù)經(jīng)濟(jì)研究，2004(4):29-32.ZHANG Lingheng.Many financial assets value at risk of copulasmeasurementmethod research［J］.Quantitative and Technica Economics，2004(4):29-32.(in Chinese)

［8］趙麗琴，籍艷麗.Copula函數(shù)的非參數(shù)核密度估計［J］.統(tǒng)計與決策，2009(9):29-32.ZHAO Liqin，JI Yanli.Copula and nonparametric kernel density estimation［J］.Statistics and Decision，2009(9):29-32.(in Chinese)

［9］Nelsen R B.An Introduction to Copulas［M］.2nd ed.New York:Springer Science Business Media，2006:7-19，157-215.

［10］Capéraà P，F(xiàn)ougères A L，Genest C.A nonparametric estimation procedure for bivariate extreme value copulas［J］.Biometrika，1997，84(3):567-577.

［11］Bücher A，Dette H，Volgushev S.New estimators of the Pickands dependence function and a test for extreme-value dependence［J］.The Annals of Statistics，2011，39(4):1963-2006.

［12］Prakasa Rao B L S.Nonparametric Function Estimation［M］.London:Academic Press Inc，1983.

［13］ ZHANG D，Wells M T，PENG L.Nonparametric estimation of the dependence function for a multivariate extreme evalue distributions［J］.Journal of Multivariate Analysis，2008，99(4):577-588.

［14］龔金國，史代敏.時變Copula模型非參數(shù)估計的大樣本性質(zhì)［J］.浙江大學(xué)學(xué)報:理學(xué)版，2012，39(6):630-642.GONG Jinguo，SHIDaimin.Large sample properties of nonparametric estimation in time-varying Copula model［J］.Journal of Zhejiang University:Science Edition，2012，39(6):630-642.(in Chinese)

［15］龔金國.Copula與非參數(shù)核密度估計［D］.成都:四川大學(xué)，2005.