一類非局部邊值條件拋物型方程組解的性質

吳春晨

(福州大學至誠學院，福建 福州350002)

文中考慮以下非線性拋物型方程組

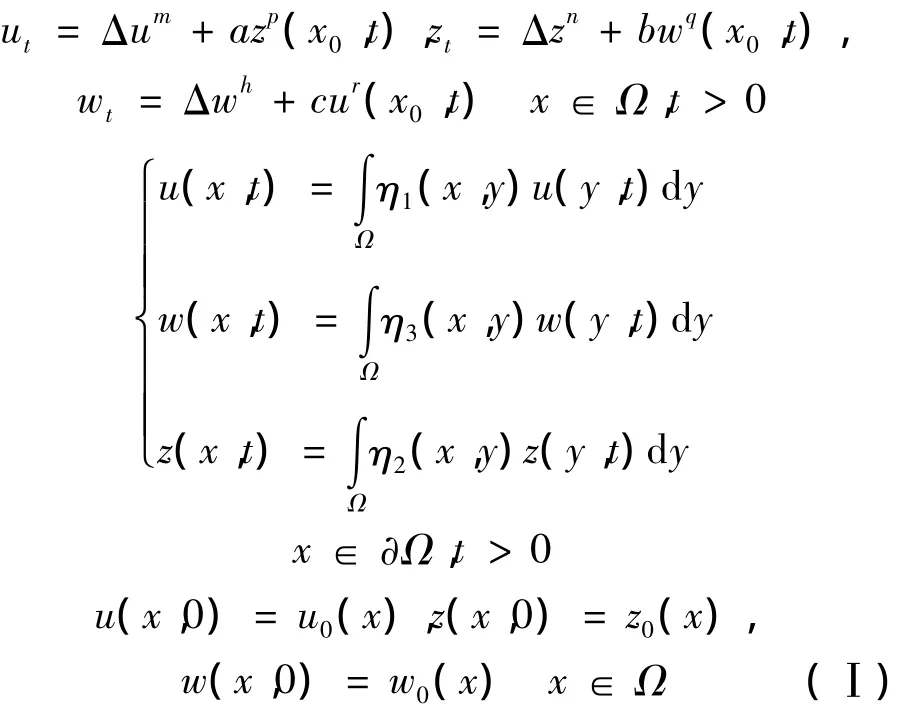
其中，m，n，h ＞ 1，a，b，c，p，q，r ＞ 0 為常數，Ω 為RN(N≥1)中的有界區域，具有光滑的邊界?Ω，η1(x，y)，η2(x，y)，η3(x，y)≠0 是對于定義在 x∈?Ω，y∈上的非負連續函數，其中(u0，z0，w0)為正的連續函數并滿足以下相容性條件:

其中，x∈ ?Ω。

近些年來，許多研究者都致力于探討帶非線性邊界條件的方程組解的性質，在熱彈性力學理論中許多重要的物理現象在模型上可以由非線性耦合的拋物型方程組描述［1－3］。Yongsheng MI等［3］討論了方程組

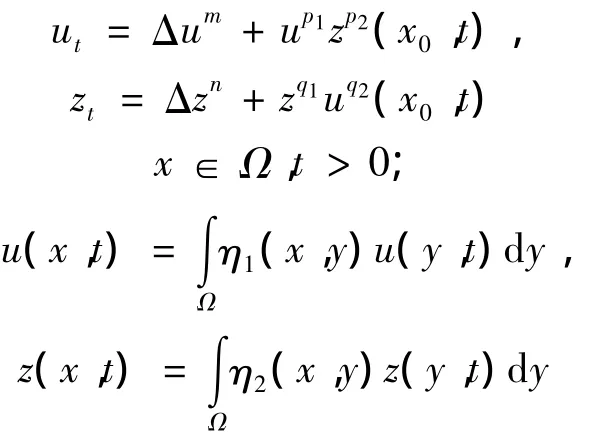
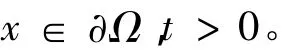
受此啟發，文中在與其相同的邊界條件與初始條件下，改變動力項，并把方程擴展為3個，即為(Ⅰ)，關于相同的動力項筆者已做系列研究［4－6］，文中，式(Ⅰ)的解(u，z，w)表示3種混合材料的溫度。

1 預備知識和定理

記 QT= Ω × (0，T)，

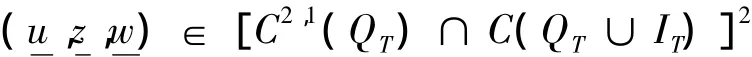
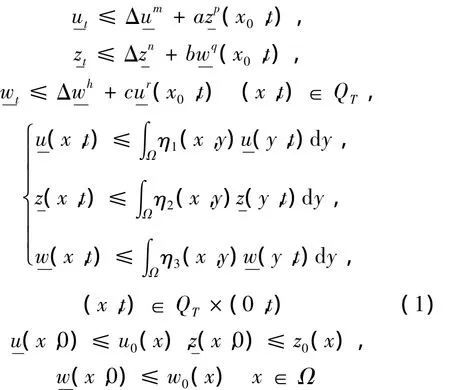
滿足如果將式(1)中的“＜”全部改為“＞”，則可得到式(Ⅰ)的一個上解的定義。比較原理 若為式(Ⅰ)在x∈中的一個非負上解和非負下解，且

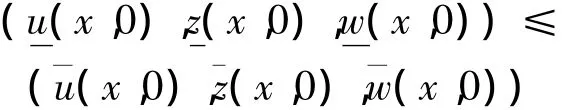
則在QT中，如果

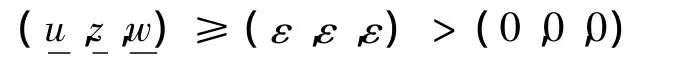
或

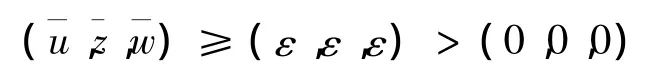
證明方法與文獻［7］相同，故略。主要結論為

定理1 設

則當pqr≤1，式(Ⅰ)存在整體解;當 pqr＞1，式(Ⅰ)的解在有限時刻爆破。

定理2 設

1)如果pqr＜mnh，則式(Ⅰ)存在整體解;

2)如果 pqr=mnh，則當 a，b，c充分小時，式(Ⅰ)存在整體解;

3)如果p，q，r ＞ 1并且pqr ＞ mnh，則當(u0，z0，w0)或者a，b，c充分小時，式(Ⅰ)存在整體解，如果(u0，z0，w0)足夠大，式(Ⅰ)的解會在有限時刻爆破。

2 整體存在性和爆破的證明

定理1證明 令(f，g，j)是以下常微分方程組的唯一解:

眾所周知，當且僅當pqr≤1，對某些正的初值(f0，g0，j0)，(f，g，j)會整體存在。如果取

則(f0，g0，j0)為式(Ⅰ)的一個上解，由于

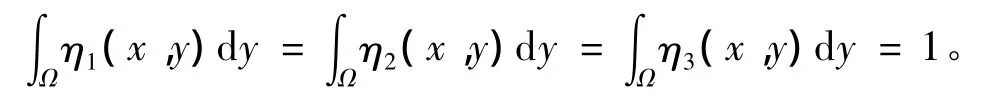
注意到

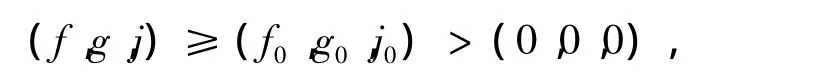
由比較原理知

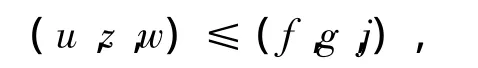
于是，當 pqr≤ 1，(u，z，w)整體存在。另外，如果取

則(f，g，j)為式(Ⅰ)的一個下解，且

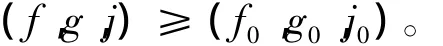
由比較原理，有

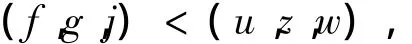
則對pqr＞ 1，(u，z，w)在有限時刻爆破，證畢。

定理2證明 令V(x)是在線性橢圓問題下唯一的正解:

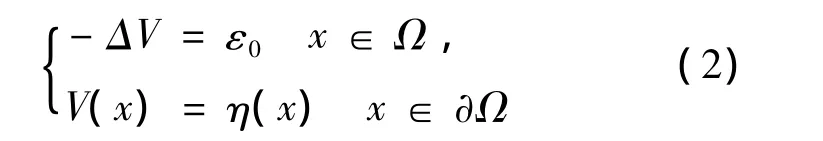
其中

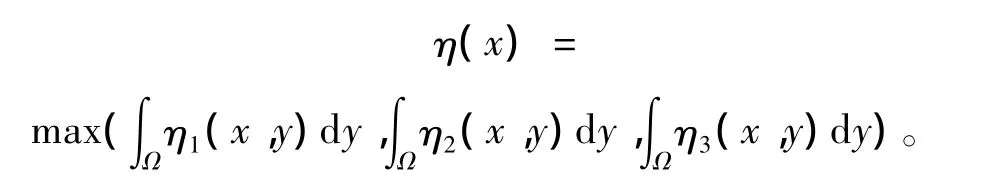
選取

使得

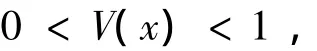
由于0＜η(x)＜1，這樣的ε0會存在。令

定義向量值函數

其中，E，l1，l2，l3＞ 0 待定，則有

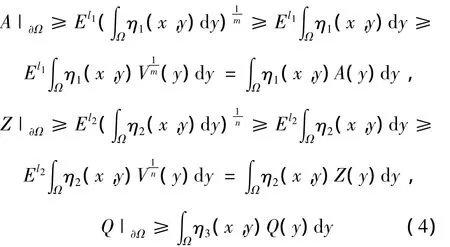
另一方面，

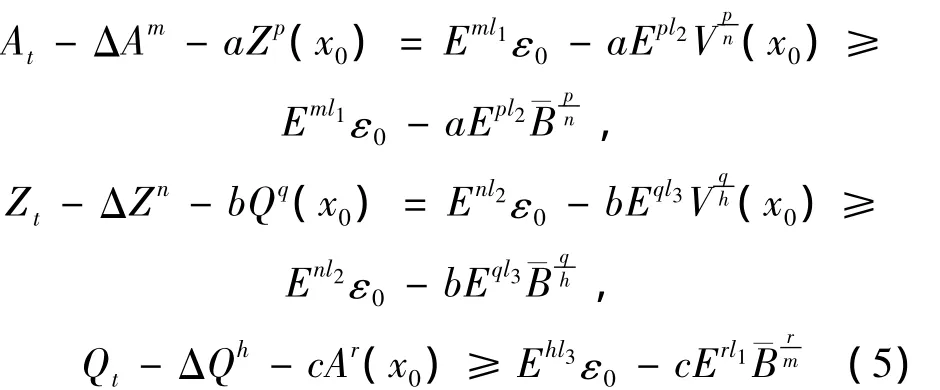
1)對于pqr＜mnh的情況，選取l1，l2＞0，l3＞0，使得

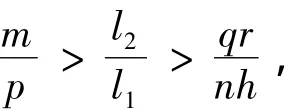
且

聯立式(4)和式(5)，取

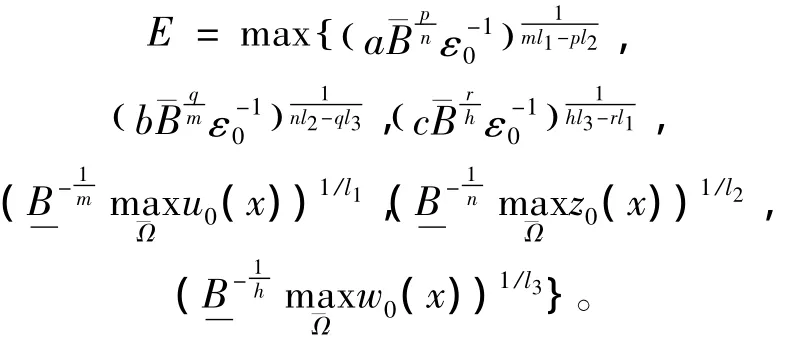
則定義在式(3)的(A，Q，Z)是式(Ⅰ)的一個上解，并且

由比較原理知，(u，z，w)≤ (A，Z，Q)，因此(u，z，w)整體存在。

2)對于pqr=mnh的情況，選取l1，l2＞ 0，l3＞0，使得

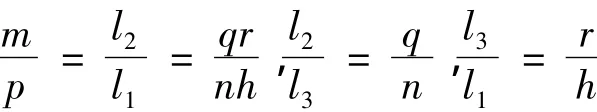
則對于任意給定的(u0，z0，w0)，選取充分大的E ＞0，使得

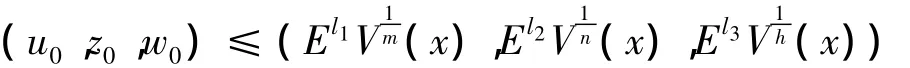
設

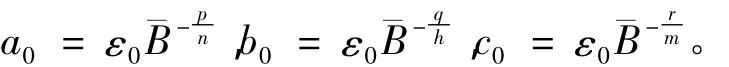
易于驗證，在 a ≤ a0，b≤ b0，c≤ c0時，(A，Q，Z)是式(Ⅰ)的一個上解。因此，由比較原理得(u，z，w)整體存在。

3)就pqr＞mnh而言，對于不同的初始值有兩種不同的結果。對于整體存在部分，相似于1)和2)的證明，首先，選取 l1，l2＞ 0，l3＞ 0，使得

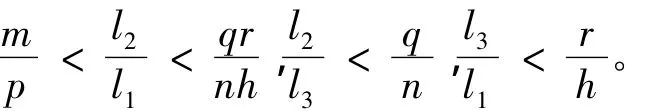
對于任意 a，b，c ＞ 0，

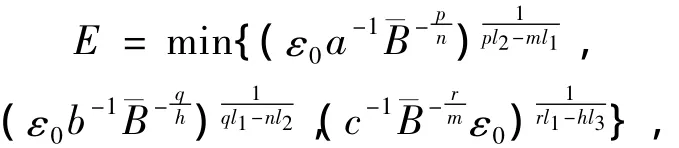
則當

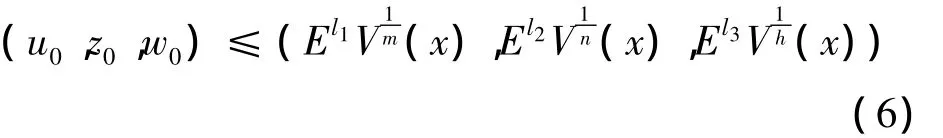
時，(A，Q，Z)是式(Ⅰ)的一個上解，由比較原理知，對于(u0，z0，w0)滿足式(6)，(u，z，w)整體存在。

另一方面，對于任意給定的初始值(u0，z0，w0)，存在適當大的常數E＞0，使得

對于這樣的一個固定的E，設

則在 a≤ a0，b≤ b0，c≤ c0時，(A，Q，Z)是式(Ⅰ)的一個上解。由比較原理知，(u，z，w)整體存在。

為了證明爆破部分，考慮以下多孔介質問題:

定理2證畢。

［1］LIHuiling.The blow-up property of positive solutions for a nonlinear parabolic equation［J］.Science in China(Series A):2007，37(3):257-273.

［2］陳玉娟.非局部退化擬線性拋物型方程組解的爆破和整體存在性［J］.數學物理學報，2011，30A(2):386-396.CHEN Yujuan.Blow-up and global existence for a nonlocal degenerate quasilinear parabolic system［J］.Acta Mathematica Scientia，2010，30A(2):386-396.(in Chinese)

［3］MIYongsheng，MU Chunlai.A degenerate parabolic system with localized sources and nonlocal boundary condition［J］.Front Math China，2012，7(1):97-116.

［4］吳春晨.一類非線性拋物型方程組正解的爆破［J］.山西大同大學學報:自然科學版，2012，23(3):5-7.WU Chunchen.The blow-up property of positive solutions for a nonlinear parabolic system［J］.Journal of Shanxi Datong University:Natural Science Edition，2012，23(3):5-7.(in Chinese)

［5］吳春晨.一類交叉耦合拋物型方程組正解的爆破性質［J］.福建工程學院學報，2012，10(6):7-10.WU Chunchen.The blow-up property of positive solutions to a class of nonlinear parabolic equations with cross-coupling［J］.Journal of FuJian University of Technology，2012，10(6):7-10.(in Chinese)

［6］WU Chunchen.Blow-up and global existence for a quasilinear parabolic system［J］.Discrete Dynamics in Nature and Society，2014，2014:1-4.

［7］Anderson JR.Local existence and uniqueness of degenerate parabolic equations［J］.Comm Partial Differetial Equations，1996，16:105-143.

［8］DU L L.Blow-up for a degenerate reaction-diffusion system with nonlinear localized sources［J］.JMath Anal Appl，2006，324:304-320.