基于擬蒙特卡羅方法的Copula-GARCH類模型在外匯風險計算中的應用
王夢媛 鄒玉梅
(山東科技大學統計與金融系,山東 青島 266590)
隨著我國外匯市場不斷發展與完善,外匯市場投資已成為繼股票市場投資后的第二大投資市場[1],因此外匯風險管理有其重要意義。為了更好的把握金融市場各外匯的風險,需運用適當的方法來刻畫金融歷史數據與波動的相關結構,同時還需在風險估計方法上加以改進。高江[2]選擇了不同類別的Pair-Copula函數構建藤Copula,運用蒙特卡羅模擬方法計算多資產投資組合的VaR,并與傳統方差-協方差風險管理方法做比較顯示更優。Niederreiter[3]系統地介紹了擬蒙特卡羅方法和偽隨機數,Levy[4]在積分計算中對比擬隨機序列與偽隨機序列并提出擬隨機序列在風險評估領域是更有效的工具。羅付巖等[5]將低差異性數列應用于金融計算中,通過數值實驗表明低維時擬蒙特卡羅方法比蒙特卡羅方法精度更高、速度快。
1 擬蒙特卡羅方法
蒙特卡羅方法產生的隨機數為偽隨機數,具有聚集性的特點,同時也有收斂速度慢、計算量大等缺陷[5]。擬蒙特卡羅方法也稱低差異序列法,它類似于蒙特卡羅方法,但它采用確定性的低差異性序列代替偽隨機數序列。擬蒙特卡羅方法避免了隨機數的聚集特性,并加快了收斂速度。由于低偏差序列所產生的點能較均勻的分布在積分區域內,從而避免了偽隨機數的聚集性。因此擬蒙特卡羅方法能很好地應用于模擬計算中[6]。本文考慮的低差異序列是Halton序列。
Halton序列的產生需要首先選出一個數M作為基底。若生成維度為i的序列,則在質數集合中取第i個質數為基底。每個自然數n都可唯一分解成下式:
其中 0≤di<M,再將上式各項系數代入式(1):
轉換后得到的Halton序列中的隨機數。
2 Copula-GARCH類模型
Copula理論的是由Sklar在1959年提出的,可以將任意一個n維聯合累積分布函數分解為n個邊緣累積分布和一個Copula函數。邊緣分布描述的是變量的分布,Copula函數描述的是變量之間的相關性[7]。
2.1 二元Copula函數的定義
二元Copula函數是具有以下性質的函數C(·,·)[8]:
(1)定義域為:I2,即[0,1]2;
(2)C(·,·)有零基面(grounded)且是二維遞增(2-increasing)的;
(3)對任意變量 u,v∈[0,1],滿足:C(u,1)=u 和 C(1,v)=v。
Sklar定理[9]:令 H(·,·)為具有邊緣分布 F(·)和 G(·)的聯合分布函數,那么存在一個 Copula 函數 C(·,·)滿足:
若 F(·),G(·)連續,則 C(·,·)唯一確定;反之 F(·),G(·)為一元分布函數,C(·,·)為相應的 Copula 函數,那么式(3)定義的函數 H(·,·)是具有邊緣分布 F(·),G(·)的聯合分布函數。
有多種方法可用于選擇適當的Copula函數族來擬合不同的相關結構,如利用λ函數、AIC準則、Kendall秩相關系數、擬合優度檢驗以及平面等高線圖等途徑。Brechmann指出對于二元Copula函數,以AIC準則作為選擇標準是可靠的[10],故本文以AIC準則作為選擇Copula函數的標準。先利用λ函數選定待選Copula函數的種類,由極大似然法估計參數后,再分別查看這些Copula函數擬合之后的AIC值,選擇其中AIC值最小的作為最終模型。
2.2 GARCH 類模型
GARCH類模型能比較好的描述金融收益率波動的動態變化特征,捕捉叢集效應和非對稱性效應[11]。GARCH(p,q)模型的一般表達式為:
式(4)、式(5)中,p≥0,q>0;ω>0,αi≥0,i=1,2,…,p,βi≥0,i=1,2,…,q.
GARCH(p,q)模型描述的收益率波動是完全對稱的,但有時收益率會呈現出一種非對稱性的特征。EGARCH模型是描述波動的非對稱效應常用模型之一。
EGARCH(p,q)模型方差方程表達式為:
式(6)中只要γ≠0就存在非對稱效應。
3 實證研究
取每日人民幣對美元、人民幣對英鎊外匯匯率中間價為樣本數據,采用對數收益率,時間范圍為2010年11月1日至2014年5月27日,共864組數據。數據來源于國家外匯管理局網站。
3.1 Copula-GARCH類模型擬合收益率分布的估計結果
由表1中J-B統計量的伴隨概率可知,在置信水平為5%時,兩種外匯收益率序列均不服從正態分布,序列表現出不同程度的尖峰厚尾性和非對稱性,且檢驗具有ARCH效應,對兩種外匯收益率序列分布進行GARCH(1,1)和EGARCH(1,1)建模。
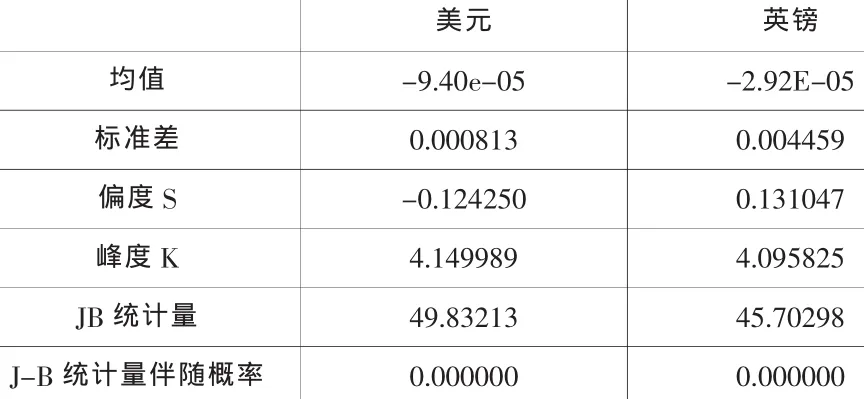
表1 外匯收益率序列的統計特性
利用GARCH類模型提取相應的標準化殘差,并對其概率積分變換后得到的序列進行K-S檢驗。從表2中可知,在5%的顯著水平下,本文所建立的GARCH類模型很好地擬合了兩種外匯收益率序列的分布。
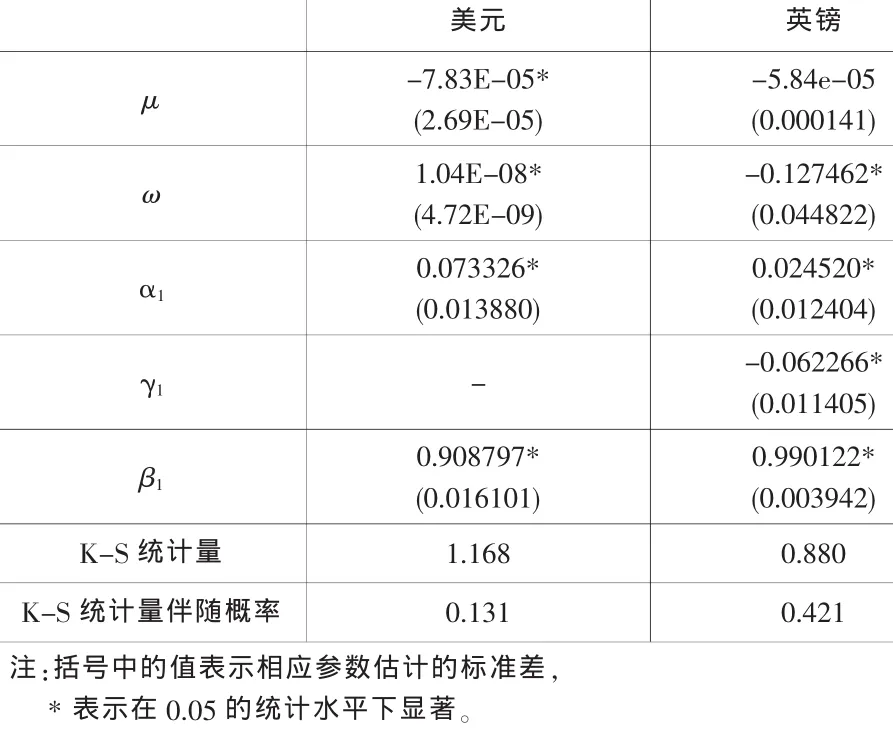
表2 GARCH類模型參數估計及K-S檢驗結果
計算兩種外匯收益率間的Kendall秩相關系數τ=-0.249,本文采用Frank Copula擬合兩種外匯的相關結構,利用極大似然估計法得到參數 θ=-2.485486。
3.2 投資組合VaR預測
投資組合中美元、英鎊權重分別為β和1-β,利用擬蒙特卡羅方法,重復模擬10000次得到所構建的Copula-GARCH類模型二維仿真數據后,將其還原為資產的收益率數據,進而得到損失序列。由損失序列的經驗分布,給定置信度1-α得到投資組合的VaR值。
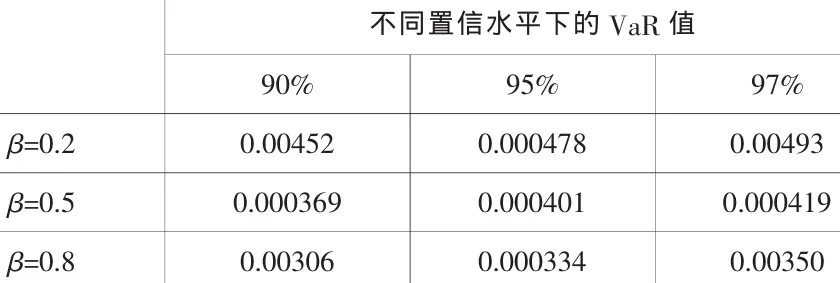
表3 VaR值的估計結果
從表3中結果可以看到在相同置信水平下,隨著美元投資比例上升,投資組合的VaR值不斷下降,這體現了美元作為國際支付、結算以及投資的主要貨幣,其價格波動的相對穩定狀態。
4 結束語
本文采用Copula-GARCH類模型對兩種外匯收益率序列相關結構進行建模。經實證研究,驗證了其收益率序列尖峰厚尾且具有條件異方差的特性,本文構建的模型達到了較好的擬合效果。同時利用Halton序列實現了對收益率數據的仿真模擬,預測了不同投資組合的VaR值。Halton序列對維數變化較敏感,其低差異特性會隨維數增加而退化,因此在模擬高維變量時可考慮采用其他低差異序列,如Fature序列和Sobol序列。
[1]張巖.外匯投資組合決策研究[D].天津:天津財經大學,2008.
[2]高江.藤Copula模型與多資產投資組VaR預測[J].數理統計與管理,2013,31(2):247-258.
[3]Niederreiter H.Quasi-Monte Carlo methods and pseudo-random numbers[J].Bulletin of the American Mathematical Society,1978,84(6):957-1041.
[4]Levy G.An introduction to quasi-random numbers[DB/OL].http://www.nag.co.uk/IndustryArticles/introduction_to_quasi_random_numbers.pdf.2002.
[5]羅付巖,徐海云.擬蒙特卡羅模擬方法在金融計算中的應用研究[J].數理統計與管理,2008,27(4):605-610.
[6]王宏梅.風險度量中的擬蒙特卡羅方法[J].中國水運:學術版,2006,6(11):159-160.
[7]韋艷華,張世英.Copula理論及其在金融分析上的應用[M].北京:清華大學出版社,2008:1-77.
[8]Nelsen R B.An Introduction to Copulas[M].New York:Springer,2006:10-11.
[9]Sklar A.Fonctions de repartition à n dimensions et leurs marges[J].Publication de l’Insititut de Statistique de l’Université de Paris,1959(8):229-231.
[10]杜子平,汪寅生,張麗.基于混合C藤Copula模型的外匯資產組合VaR研究[J].技術經濟與管理研究,2013,32(6):99-103.
[11]龔銳,陳仲常,楊棟銳.GARCH族模型計算中國股市在險價值(VaR)風險的比較研究與評述[J].數量經濟技術經濟研究,2005(7):67-81.

