獨立驅動電動汽車穩定性的滑模變結構控制*

林 程，彭春雷,2，曹萬科

(1.北京理工大學機械與車輛學院，北京 100081；2.中國北方車輛研究所，北京 100072)

?

2015024

獨立驅動電動汽車穩定性的滑模變結構控制*

林 程1，彭春雷1,2，曹萬科1

(1.北京理工大學機械與車輛學院，北京 100081；2.中國北方車輛研究所，北京 100072)

為充分利用雙電機獨立驅動電動汽車兩側電機獨立可控這個特點來提高車輛穩定性，在研究汽車動力學與穩定性特點的基礎上，利用MATLAB/Simulink建立了包括任意路徑下的單點預瞄駕駛員模型和“魔術公式”輪胎模型在內的8自由度的“人-車”閉環動力學仿真平臺。運用滑模變結構控制原理，分別設計了以兩側電機為執行機構，以橫擺角速度、質心側偏角和橫擺角速度與質心側偏角聯合為控制變量的3種等速趨近滑模變結構控制器，在仿真平臺進行了穩定性控制的仿真。結果表明，3種控制器均可有效提高汽車極端工況下的操縱穩定性，其中，又以橫擺角速度與質心側偏角為聯合控制變量的控制器效果最好。

獨立驅動電動車；穩定性控制；駕駛員模型；滑模變結構控制器

前言

節能、環保、安全是汽車發展的三大主題，作為汽車主動安全重要技術的電子穩定程序ESP(或ESC、VDC)受到越來越多的關注，目前ESP主要通過3種方式來實現汽車的穩定性控制：調整轉向角[1]、調整垂向載荷和調整驅動制動力。

調整轉向角進行穩定性控制，只在汽車的線性范圍內比較有效；調整垂向載荷進行穩定性控制，只適用于裝有主動懸掛的汽車，而且也只有在很大的側向加速度或側傾角時才有效；隨著ABS和TCS的發展，控制汽車的制動力和驅動力比較容易，而制動力和驅動力的控制對汽車的具體設計也沒有特殊要求。因此目前多采用第3種方法，即通過對制動力和驅動力的控制來實現汽車的穩定性控制。

傳統內燃機汽車通過驅動進行穩定性控制比較復雜而且難以實現精確控制，而雙電機獨立驅動電動汽車的兩個驅動電機獨立可控，且響應快速準確，通過驅動力來控制汽車的穩定性將強化目前的TCS和ESP功能，有助于增強汽車的操縱穩定性和行駛安全性。

在獨立驅動電動汽車的穩定性控制方面，國內外許多學者進行了相關研究。文獻[2]中對后輪獨立驅動電動汽車的操縱穩定性控制進行了研究，建立了質心側偏角前饋控制和質心側偏角與橫擺角速度的狀態反饋控制模型，并通過主動干預車輪縱向力來直接產生橫擺力矩進行穩定性控制。文獻[3]中研究了四輪獨立驅動電動汽車穩定性控制，以橫擺角速度和質心側偏角為控制變量，基于模糊控制建立了差動驅動/制動的穩定性控制系統。文獻[4]中對四輪獨立驅動-獨立轉向(4WID- 4WIS)車輛橫擺穩定性控制進行了研究，以橫擺角速度和質心側偏角為控制變量，基于模糊控制提出了集成“主動前/后輪轉向+直接橫擺力矩控制”的車輛橫擺穩定性控制系統。以上研究都取得了較好的控制效果，但都需要大量的實驗和豐富的經驗。由于汽車行駛路面與行駛工況極其復雜，這些控制算法很難包括各種工況。鑒于其對控制系統參數和外部擾動不敏感的特點，文獻[5]～文獻[7]中都采用滑模變結構控制(sliding mode control, SMC)，對四輪驅動電動汽車穩定性控制進行了研究，分別設計了以質心側偏角、橫擺角速度以及兩者聯合為控制變量的穩定性控制策略，取得了較好的控制效果，但是在控制過程中僅考慮了控制變量的誤差，沒有考慮控制變量誤差的變化率。據此，本文中采用高階滑模控制器，同時考慮控制變量誤差和誤差變化率，設計了3種以驅動電機為執行機構的等速趨近滑模變結構控制器，并進行了仿真。結果表明，3種控制率均可有效抑制系統未建模動態和外部擾動，具有很好的魯棒性，從而提高了汽車的操縱穩定性，聯合控制效果很好。

1 雙電機獨立驅動車輛動力學模型

1.1 整車動力學模型

建立汽車動力學模型時，既要全面考慮影響汽車操縱穩定性的主要因素，以真實地表示汽車的動力學特性，同時又要盡量簡單以滿足實時計算要求。穩定性分析、控制方法研究中采用2自由度參考模型；方法驗證部分采用8自由度整車模型，包括縱向、側向的平動自由度，繞垂直軸的轉動自由度，4個車輪的旋轉自由度和前輪的轉角自由度。

整車動力學微分方程如下：

(1)

(2)

(3)

式中：m為車輛總質量；vx為車輛縱向速度；vy為車輛側向速度；ωr為車輛橫擺角速度；∑Fx為車輛受到的縱向力；∑Fy為車輛受到的側向力；Iz為車輛繞z軸的轉動慣量；∑Mz為車輛受到繞z軸的橫擺力矩；ΔM為主動干預所產生的附加橫擺力矩，由兩個前驅動輪通過調節縱向力產生。

(4)

式中：B為前輪距；ΔFx1為主動干預時左前輪縱向力變化量；ΔFx2為主動干預時右前輪縱向力變化量；并且ΔFx1=-ΔFx2，因此ΔM=BΔFx2=-BΔFx1。

1.2 電機模型與傳動系統模型

1.2.1 電機模型

雙電機獨立驅動電動汽車需要匹配兩臺電機，但車輛內部空間有限，運行工況復雜，而且汽車的動力性、經濟性和續駛里程等指標要求較高，所以選擇同時具有高功率密度、高效率和高可靠性的永磁同步電機。此外，永磁同步電機還兼備發電機的功能，既可進行電驅動，又可進行電制動，正好符合電動汽車的多方面需求。

通常采用的電機模型有數學模型和經驗模型兩種。經驗模型計算量小，而且使用方便，故采用經驗模型。經驗模型中電機的輸出轉矩根據電機當前的轉速和踏板行程通過查表確定，可表示為

Tm=f(θA,n)

(5)

式中：Tm為電機輸出轉矩；n為電機的轉速；-1≤θA≤1，車輛行駛時，θA>0，其數值表示加速踏板的歸一化行程；車輛制動時，θA<0，其數值表示制動踏板的歸一化行程。

所采用電機的最大轉矩Tmax=78N·m，額定轉速為1 960r/min，并且假定電機驅動和制動時的轉矩特性一致。電機的轉矩特性如圖1所示。

1.2.2 傳動系統模型

雙電機獨立驅動電動汽車的驅動力由電機直接通過具有固定減速比的減速器傳遞至車輪，因此，兩驅動輪的驅動轉矩為

Tmdj=Tmjiη

(6)

式中：Tmj為電機輸出轉矩，j=1,2分別表示左前輪和右前輪；Tmdj為驅動輪上的驅動轉矩；i為傳動系統的總傳動比；η為傳動系統的傳動效率。

獨立驅動電動汽車左右兩側的動力系統和傳動系統均一致，因此傳動比和傳動效率一樣。

1.3 車輪動力學模型

以左前驅動輪為例，其受力分析如圖2所示。

圖中：Tmd為電機傳遞到車輪的驅動轉矩；ΔM′為附加橫擺力矩傳遞到車輪的轉矩；v1為輪心縱向速度；ω為車輪旋轉角速度；Fx為車輪縱向力；Fz為車輪的垂向載荷。

根據受力情況車輪旋轉運動的微分方程為

(7)

式中：Iω為車輪的轉動慣量；r為車輪半徑。

1.4 輪胎動力學模型

輪胎模型在車輛操縱穩定性控制中起著重要的作用，“魔術公式”通過一個公式即可表示出縱向力、側向力以及回正力矩，公式中的參數具有一定的物理意義，便于理解，簡單易用。本文中采用“魔術公式”輪胎模型[8]進行動力學仿真分析。

1.5 駕駛員模型

為驗證控制方法的效果，須進行一系列典型的仿真和測試，如雙移線、蛇形試驗，要進行這些試驗必須使車輛按照預定的軌跡行駛，因此，須建立駕駛員任意路徑跟蹤模型。本文中采用單點預瞄理論建立了任意路徑跟隨駕駛員模型，如圖3所示，其中各參數的意義詳見文獻[9]和文獻[10]。

2 滑模變結構控制器設計

2.1 控制變量及其期望值的確定

若車輛沿前進方向的速度視為定值，側向加速度限定在0.4g以下，則輪胎側偏特性處于線性范圍；同時假定驅動力不大，不考慮地面切向力對輪胎側偏特性的影響時，2自由度整車模型的微分方程為

(8)

式中：β為車輛的質心側偏角；Cf、Cr分別為前后輪胎的側偏剛度；δf為前輪轉角；a、b分別為車輛質心和前、后軸在地面投影的垂直距離。

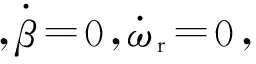
(9)

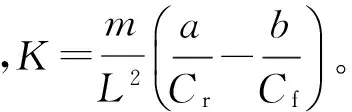
車輛轉向過程中側向加速度受到輪胎在路面上附著能力的限制，不能超過路面所能提供的側向加速度極限值。因此，橫擺角速度的上限值為

(10)

式中：μ為路面附著系數；ωrmax為最大橫擺角速度。

從而式(9)中的理想橫擺角速度修正為

(11)

根據式(9)有

(12)

由式(10)和式(12)得質心側偏角的上限為

(13)

式中βmax為車輛最大質心側偏角。

從而式(9)中的理想質心側偏角修正為

(14)

由式(9)可得期望的橫擺角速度和期望的質心側偏角存在如下關系：

(15)

由式(15)可知，兩個被控變量的期望值是相互耦合的，與車速、質心位置和輪胎側偏剛度有關。本文中選擇ωr、β和ωr與β同時作為控制變量，分別對這3種情況進行控制分析。

2.2 滑模面的確定與控制率的分析

控制系統設計以線性2自由度模型為基礎，所設計的控制系統是根據不同的控制算法對整車施加附加橫擺力矩，因此2自由度模型可變為

(16)

滑模變結構控制的趨近率[11]包括等速趨近率、指數趨近率、冪次趨近率和一般形式趨近率。其中，等速趨近率運算量較小，且魯棒性好，故選擇等速趨近率。

2.2.1 橫擺角速度控制

橫擺角速度控制的跟蹤誤差及其導數為

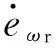
定義滑模面為

(17)

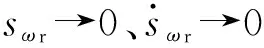
(18)

式中ΔMωr為采用橫擺角速度控制時所需要的附加橫擺力矩。

根據系統可達到的條件，確定橫擺角速度控制的附加橫擺力矩為

(19)

式中Kωr為橫擺角速度控制的趨近速度，為常量，且Kωr>0。當Kωr太小時，趨近滑模面的時間比較長；當Kωr太大時，又會產生嚴重的抖振，因此應根據滑動條件選取適當值。

為降低系統抖振的影響，將式(19)中的符號函數替換為飽和函數[11]，即

(20)

式中Δωr>0為邊界層，可以根據高頻抖振情況選取適當的邊界層厚度；kωr為常數；當sωr處于邊界層外部時，采用開關控制，當sωr處于邊界層內部時采用線性反饋控制。

2.2.2 質心側偏角控制

定義滑模面為

(21)

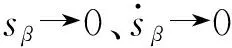
(22)

(23)

式中Kβ為質心側偏角控制的趨近速度，Kβ>0。

2.2.3 橫擺角速度和質心側偏角聯合控制

定義滑模面為

(24)

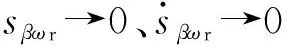
(25)

(26)

式中Kβωr為橫擺角速度和質心側偏角聯合控制的趨近速度，且Kβωr>0。

2.3 滑模變結構控制系統穩定性分析

以橫擺角速度為例分析控制系統的穩定性。定義Lyapunov函數為

(27)

可以得到

(28)

將ΔMωr代入式(28)得：

(29)

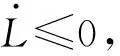
3 基于駕駛員預瞄跟隨模型的人車閉環系統仿真

為驗證上述控制方法的有效性，根據前面所建立的動力學模型和控制器，在MATLAB/Simulink環境下進行了仿真。車輛的主要參數為：

m=1 350kg,Iz=1 975kg·m2,a=1.085m,

b=1.386m,Cf=Cr=45kN/rad,B=1.429m,

Iω=0.87kg·m2,r=0.289m，i=7.02。

蛇行試驗常用來評價汽車行駛的穩定性，不僅可以反映出人車閉環系統進行快速大角度轉向的能力，同時也可反映在快速大角度轉向時車輛的操縱穩定性和行駛安全性。為了測試控制方法的性能，利用建立的人-車閉環系統參照國標GB/T 6323.1—94中的規定進行蛇行試驗仿真。仿真工況為高附著系數路面(μ=1)、80km/h，車輛行駛過程中轉向盤轉角根據預瞄跟隨理論由駕駛員模型給出，如圖4所示，仿真結果如圖5～圖10所示。圖5中，“o”表示蛇行試驗的標樁。

從圖5、圖6和圖7可以看出，3種SMC控制均能使車輛按照預定軌跡行駛，使車輛的側向軌跡保持能力增強，同時有效地改善了質心側偏角和橫擺角速度的狀態。從圖8和圖9可以看出，表征車輛穩定狀態的橫擺角速度和質心側偏角均在可控范圍內，并且無論汽車從何處開始運動，最終都會收斂到控制系統的滑模面上，使系統保持穩定。3種SMC控制方法相似，圖10為質心側偏角與橫擺角速度聯合控制時驅動轉矩變化情況，可以看出：不進行主動控制時，為了克服彎道行駛阻力驅動轉矩的不斷變化，兩側電機采用等轉矩控制方式；進行主動控制時，主動控制系統根據橫擺角速度和質心側偏角的偏差程度進行判斷，當偏差小于設定閾值時不進行主動干預，當偏差大于閾值時進行主動干預，當需要的附加橫擺力矩較小時，兩側電機同時驅動，但驅動轉矩大小不同，并且利用驅動力的差值產生所需的附加橫擺力矩，當需要的附加橫擺力矩較大時，為了車輛的穩定性和安全性，兩側電機一個進行電驅動，另外一個進行電制動，從而產生所需的附加橫擺力矩。另外，從圖5～圖9可以看出，在高附著路面上3種SMC控制均能有效提高車輛的穩定性，而質心側偏角與橫擺角速度聯合控制的效果比其它兩種控制方式更優。

4 結論

基于大曲率任意路徑下的單點預瞄駕駛員模型和“魔術公式”輪胎模型，建立了8自由度的“人-車”閉環汽車動力學仿真平臺，用于進行車輛穩定性控制研究。通過對不進行穩定性控制和3種SMC穩定性控制仿真分析的研究表明，3種SMC控制器均可有效提高汽車的操縱穩定性，而聯合控制的效果更好。

[1] Nam Kanghyun, Oh Sehoon, Hori Yoichi.Robust Yaw Stability Control for Electric Vehicles[C].IEEE Vehicle Power and Propulsion Conference, VPPC 2010,2010.

[2] Shino M, Nagai M.Independent Wheel Torque Control of Small-scale Electric Vehicle for Handling and Stability Improvement[J].JSAE Review,2003,24:449-456.

[3] Li Feiqiang,Wang Jun,Liu Zhaodu.Fuzzy-logic-based Controller Design for Four-wheel-drive Electric Vehicle Yaw Stability Enhancement[C].Proceedings of the 2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery, FSKD 2009:116-120.

[4] 楊福廣,阮久宏,李貽斌,等.4WID-4WIS車輛橫擺運動AFS+ARS+DYC模糊控制[J].農業機械學報,2011,42(10):6-12.

[5] 王偉達,張為,丁能根,等.汽車DYC系統的二階滑模控制[J].華南理工大學學報,2009,39(1):141-146.

[6] Massimo Canale, Lorenzo Fagiano, Antonella Ferrara, et al.Vehicle Yaw Control via Second-Order Sliding-Mode Technique[J].IEEE Transactions on Industrial Electronics,2008,55(11):3908-3916.

[7] 趙艷娥,張建武.基于滑模控制的四輪驅動電動汽車穩定性控制[J].上海交通大學學報,2009,43(10):1526-1530.

[8] Bakker E, Pacejka H B, Lidner L.A New Tire Model with an Application in Vehicle Dynamics Studies[C].SAE Paper 890087.

[9] 郭孔輝.駕駛員-汽車閉環系統操縱運動的預瞄最優曲率模型[J].汽車工程,1984,6(3):1-16.

[10] 郭孔輝.預瞄跟隨理論與人-車閉環系統大角度操縱運動仿真[J].汽車工程,1992,14(1):1-11.

[11] 劉金琨,王新華.機械系統先進滑模變結構控制:設計、分析及MATLAB仿真[M].北京:清華大學出版社,2011:19-25.

Sliding Mode Variable Structure Control for the Stability ofIndependent Drive Electric Vehicle

Lin Cheng1, Peng Chunlei1,2& Cao Wanke1

1.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081; 2.ChinaNorthVehicleResearchInstitute,Beijing100072

For fully taking the advantage of the feature of independence and controllability of two side motors in two-motor independent drive electric vehicle to enhance its stability, an eight-DOF human-vehicle closed-loop dynamics simulation platform is set up, incorporating single-point preview driver model for arbitrary path and ‘magic formula’ tire model.Based on sliding mode variable structure control theory, three different sliding mode variable structure controllers with constant approaching rate are designed with two side motors as actuators and yaw rate, mass-center sideslip angle and both yaw rate and mass-center sideslip angle as control variables respectively.The results of stability control simulation show that all three different controllers can effectively enhance the handling stability of vehicle in extreme working conditions, among which, the controller with both yaw rate and mass-center sideslip angle as control variables achieves the best results.

independent drive electric vehicles; stability control; driver model; sliding mode variable structure controller

*國家自然科學基金(51175043)資助。

原稿收到日期為2012年10月24日，修改稿收到日期為2013年4月4日。