語言網絡研究的數(shù)學模型——從復雜網絡、社會網絡到語言網絡

趙懌怡，劉海濤

（1.廈門大學人文學院，福建廈門361005；2.浙江大學外國語言文化與交流學院，浙江杭州310058）

1 引言

復雜網絡技術的發(fā)展為語言研究提供了新的視角和手段。“把語言視為網絡”具備語言學、認知科學、心理學的理論依據(jù)［1］。目前可見語言網絡的研究涉及語言符號的字單元、詞單元［2］、句法［3－6］、語義［7－8］等多層級符號系統(tǒng)，網絡構建與研究的目的除了探索各層級符號對應語言網絡之間的差異，還包括探索各類語言網絡構建的理據(jù)性與網絡結構共性［9－10］，但鮮有關于復雜網絡、社會網絡、語言網絡重要規(guī)律的綜述。語言網絡研究科學化的主要目的是發(fā)現(xiàn)事物的發(fā)展規(guī)律，以模型的形式重復驗證與預測事物的發(fā)展［11］，以此為目標本文綜述了迄今從復雜網絡到社會網絡、語言網絡領域的主要數(shù)學模型，嘗試為語言網絡普適價值提供參考。

2 網絡初步：圖論

進入到語言網絡研究的操作階段，圖論是打開語言復雜網絡研究之門的第一把鑰匙［12－14］。網絡是節(jié)點的集合，所以定義［X］k表示元素為k的集合X。一個簡單的無向圖G表示為G＝（V，E）；V表示圖G節(jié)點集合，E表示邊的集合，E?｜［V］2｜；定義G＝（X，Y）為圖G，則有V（G）＝X，E（G）＝Y；若有邊e2＝｛v，w｝∈E，則表示邊e2以節(jié)點v，w為頂點，同時v，w互為相鄰節(jié)點（adjacent neighbors），如果兩條邊e1，e2有共享公共節(jié)點，也可以說兩條邊互為相鄰邊。E（v）是以v為頂點的邊的集合。N（v）是節(jié)點v的鄰節(jié)點集合。以上是圖1所示無向圖G的組成元素的基本定義。

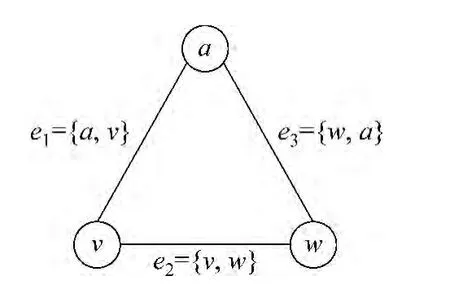
圖1 無向圖示例，G＝（V，E），V＝｛a，v，w｝，E＝｛e1，e2，e3｝，G＝（X，Y），X＝3，Y＝3，E（a）＝｛e1，e3｝，N（a）＝｛u，w｝，d（G）＝2

在一個擁有更多節(jié)點的網絡G中，節(jié)點vi的節(jié)點度表示為d（vi）＝ki，ki也反映圖中節(jié)點的連通性，反映節(jié)點鄰里規(guī)模。節(jié)點vi節(jié)點度ki也等于節(jié)點vi的邊集合｜E（vi）｜，｜E（vi）｜表示所有以vi為頂點的邊數(shù)。很明顯，在圖1所示無向圖G中，｜E（w）｜＝｜N（w）｜，｜E（v）｜＝｜N（v）｜，｜E（a）｜＝｜N（a）｜。這表明E是不包含多重邊的集合。在包含多重邊的網絡中，多重邊可以通過賦予邊值來表示，包含多重邊的圖通常被稱為加權圖或加權網絡。

對于整個網絡G來說，平均節(jié)點度（average node degree）可以表示為：

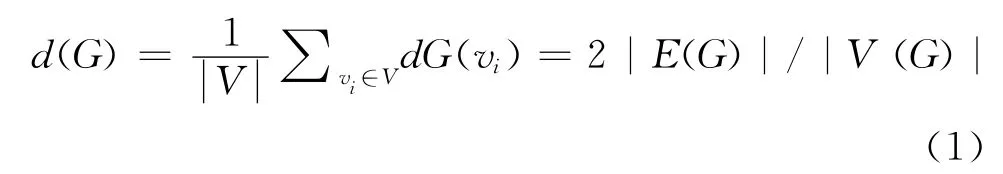
平均節(jié)點度反映網絡中節(jié)點的平均連通性。衡量此問題的標準化參數(shù)是網絡密度（density）D（0＜D＜1）。密度為0的網絡是一個無邊相連、節(jié)點孤立的網絡，相反，一個節(jié)點完全連通的網絡密度為1。孤立節(jié)點數(shù)提供了一個考察網絡密度分布的視角。另一個反映密度的相關參數(shù)是網絡中心度（centralization）。一個星形狀拓撲的網絡中心度接近1，分散的網絡中心度接近0。

路徑長度（path length）是形成節(jié)點間路徑的邊數(shù)。網絡中指定兩個節(jié)點可能有多條路徑相連。如圖1示例，圖G有節(jié)點v，w，它們可以通過兩條路徑L（v，w）＝｜e2｜＝1，L（v，w）＝｜e1＋e3｜＝2相連。其中，L（v，w）＝｜e2｜為兩個節(jié)點間的距離，是兩個節(jié)點最短的路徑長度（shortest path length），節(jié)點v和w（v≠w）的距離表示為（distance）δ（v， w）＝1。

用P表示無向圖中所有節(jié)點間距離的集合，無向圖直徑D（G）是任意兩個節(jié)點間最大的最短路徑長度，即P中最大δ。平均最短路徑通常被稱為網絡的平均路徑長度。所有節(jié)點間路徑長度的均值為網絡的平均路徑長度（average path length）表示為L（G）。

以語言網絡為例來說明，如圖2所示，G1是一個由詞為節(jié)點根據(jù)句子“ROOT人體，是，由，數(shù)以億計，的，微小，而，有，生命，的，細胞，構成，的ROOT，這，些，細胞，構成，各，個，不同，的，組織，器官，保證，了，人體，的，正常，工作”中詞的前后鄰接的同現(xiàn)關系①同現(xiàn)網絡是根據(jù)詞的上下文同現(xiàn)關系構造的網絡，是語言工程領域最常見的構造語言網絡方法。構成的無向圖，節(jié)點集合V＝｛這，些，各，個，……，細胞，構成｝，邊集合E＝｛e這些，e些各，e各個，……e細胞，e構成｝，G1的值表示為｜G1｜＝｜V1｜＝23（節(jié)點數(shù)），｜E1｜＝29（邊數(shù)）。NG1（些）＝｛這，細胞｝，dG1（些）＝｜E（些）｜＝｜NG1（些）｜＝2。δ（這，些）＝1。直徑D（G1）＝5。

有向圖G2（圖3）相比無向圖G1最為明顯的變化就是節(jié)點度分化為出度、入度。例如，dG2（的）＝｜E（的）｜＝｜NG2（的）｜＝kin（的）＋kout（的）＝9，kin（的）＝4，kout（的）＝5。

通過PAJEK②社會網絡分析工具。獲得示例網絡G1和G2的基本參數(shù)（表2），發(fā)現(xiàn)相同節(jié)點和邊構成的無向網絡和有向網絡在平均路徑長度、直徑、網絡密度、節(jié)點度方面存在差異。以同現(xiàn)網絡為例的概念解釋和參數(shù)比較說明，用語言材料不同顆粒的單位構建網絡是可行的且有差別的［15］。

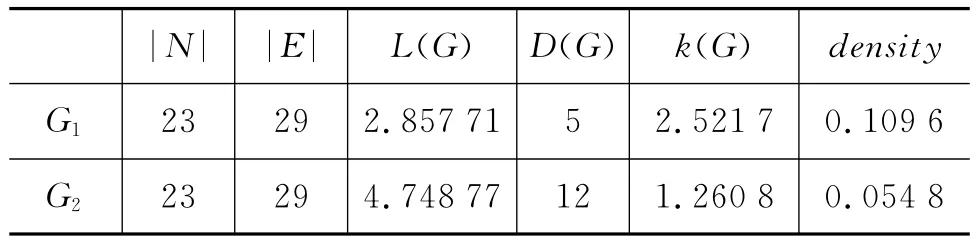
表2 G1和G2的基本參數(shù)

網絡科學是一門以物理學為基礎的分支學科，但其發(fā)展受到社會學的重要影響。網絡科學的重要組成復雜網絡和復雜科學的發(fā)展就是源于社會網絡的研究。社會網絡注重計量角度考察網絡特征［16］。除了觀察網絡基本參數(shù)節(jié)點度、平均路徑長度、聚集系數(shù)之外，網絡密度、網絡中心度和網絡凝聚度（cohesion）［17］也是社會網絡研究的焦點，社會網絡借此來考察更為局部的網絡的組成（components）和網絡中的次集團（cliques）現(xiàn)象。

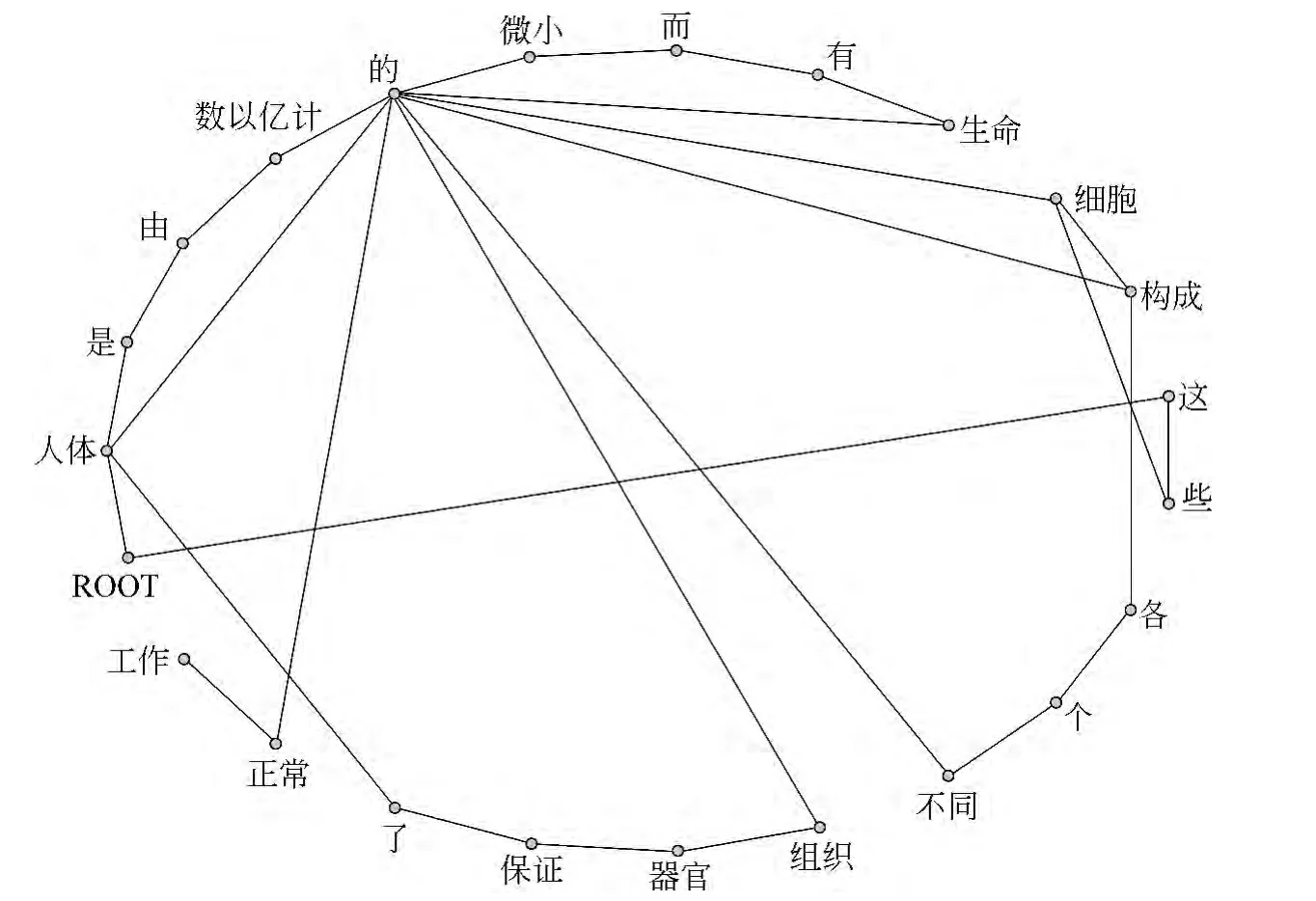
圖2 （同現(xiàn)網）無向圖例G1

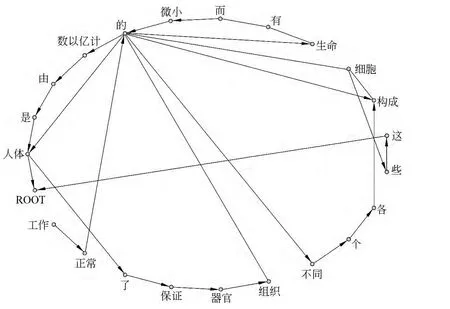
圖3 （同現(xiàn)網）有向圖例G2

3 小世界網絡

歐拉（Eüler）開創(chuàng)圖論學科促成了網絡科學的興起，網絡科學接下來的重要發(fā)展始于20世紀中葉由Solomonoff和Rapopor［18］以及Erd?s和Rényi［19］引入的隨機網絡。網絡是由節(jié)點和連線組成的圖，成分簡單，但是卻能呈現(xiàn)高度的復雜性。20世紀以來的大量研究證明了隨機網絡并不能描述真實網絡的拓撲特性。而自然界的從技術到生物乃至人類社會中的各種開放系統(tǒng)都表現(xiàn)為更為復雜的網絡形式。20世紀末統(tǒng)計物理學出現(xiàn)的小世界網絡［20］和無標度網絡［21］開啟了網絡科學中對于復雜網絡特性的探索。

小世界特征（Small World）是區(qū)分隨機網絡和大規(guī)模復雜網絡的可測特征。該研究開始于Milgram［22］，Milgram最初關注人們和他們熟人間的社會網絡關系，即在特定人群中，兩個人如何實現(xiàn)聯(lián)系的最短連接。Wasserman和Faust［23］研究讓一個人通過熟人傳遞的方式把一封信寄給目標人，在這樣的社會網絡中，網絡結合度（和網絡信息流動高效性、脆弱性有關的參數(shù)）顯現(xiàn)出來。在Milgram的模型（short－cut property）中，網絡中兩個隨機節(jié)點間的最短路徑可以被視作小世界網絡的指標。但這個單一指標并不能成為社會網絡區(qū)別于隨機網絡（也有最短路徑特征）的特征。作為補充，Watts和Strogatz［20］提出了兩個特征奠定了小世界網絡的基礎：相比于隨機網絡，小世界網絡有更高的聚集系數(shù)；相比于隨機網絡，小世界網絡有近似的最短路徑。

為了解釋這個問題，Watts和Strogatz［20］引用了兩個指標：聚類（clustering）和密度。在無向網絡中，聚類是節(jié)點vi∈V（G）的聚集度（cluster value）Cvi（G）的均值。更為準確地說，節(jié)點的聚類等于節(jié)點vi的實際邊數(shù)adj（vi）與相應完全圖｜NG（vi）｜中節(jié)點vi邊數(shù)的平均比值：

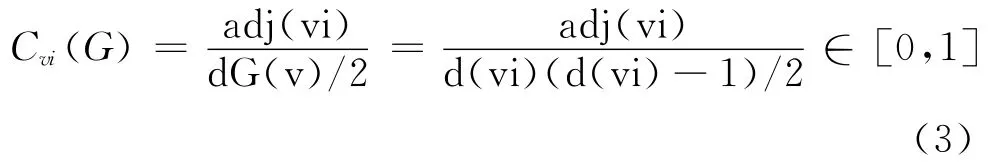
那么整個圖G的聚集度CWS（G）可以定義為：

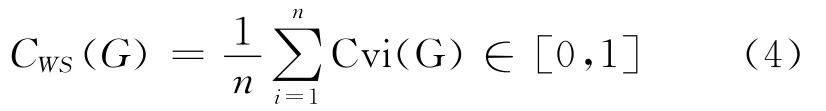
所以CWS描述一個網絡中節(jié)點相互連接的程度。聚類和社會網絡的傳遞性相關。CWS的缺陷是不能很好地在多重邊的圖中操作。原因是：兩個節(jié)點間如果有多條邊，邊數(shù)只能計算一次。因此，Bollobás和Riordan［23］提出了聚集系數(shù)（cluster coefficient）CBR（G），用來表示網絡中三角關系數(shù)量（number of triangles）和相鄰邊數(shù)量（number of pairs of adjacent edges）的比值：

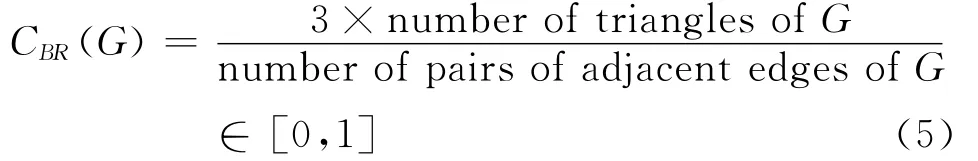
高聚集系數(shù)CBR（G）和聚集度CWS（G）一樣，表示圖G的聯(lián)結是可傳遞的，如果某節(jié)點u∈V（G）和節(jié)點a，w∈V（G）相連接，那么節(jié)點a，w也可能是相連的。在一個好友網絡中，高聚集系數(shù)意味著一個人甲的朋友乙的朋友丙也可能是甲的朋友。很明顯，聚集系數(shù)的概念并沒有與聚集度分析混淆，但在某種程度上是相似測量。

Watts和Strogatz［19］考察的核心是規(guī)則網絡具有高聚集度，隨機網絡有低聚集度，聚集度的分布相反于平均路徑長度，聚集系數(shù)越大網絡的平均路徑長度越小。Bollobás和Riordan［24］指出盡管平均路徑長度小于或等于網絡直徑，但是平均路徑長度比起直徑并非小很多。因此平均路徑長度可以作為小世界的測度之一。

從L（G）和CWS（G）的角度，Watts和Strogatz［20］細化了小世界的概念（此后小世界被稱作WS model）。小世界網絡表現(xiàn)出類似規(guī)則網絡較高的聚集度和類似隨機網絡較小平均路徑長度：

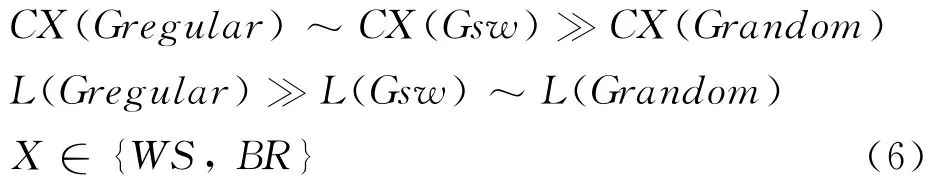
L（G）表示網絡的平均路徑長度，L（G）顯示了“全局網絡特征”，它聚合了網絡所有成對節(jié)點的相關性。相比之下，CWS（G）表示“局部網絡特性”。按照這個標準，語言網絡呈現(xiàn)出小世界的特性。研究表明，漢語詞同現(xiàn)網絡與英語詞同現(xiàn)網絡一樣，平均最短路徑遠小于網絡規(guī)模而聚集系數(shù)非常高，具有明顯的小世界效應［4］。漢語句法、語義網絡和ER隨機網絡①Erd?s和Rényi（1961）引入的隨機網絡模型。的平均路徑長度和直徑大致相當，但句法網絡的聚集系數(shù)要遠遠大于ER隨機網絡，漢語句法、語義網具有小世界特征［8，25］。

但小世界的模型也存在缺陷，在于L（G）和CWS（G）關注相應輸入值的某一時刻（靜態(tài)）的分布，丟失了對這個分布更為細節(jié)的描述。而無標度模型可以用來彌補這個缺陷。

4 無標度網絡

小世界模型描述網絡靜態(tài)特征，而小世界網絡動態(tài)增長特征被描述為擇優(yōu)模型（preferential attachment model）［21］，后來也被稱為BA模型（Barabási－Albert model，BA model）。Barabási和Albert觀察到：復雜網絡節(jié)點連通根據(jù)無標度規(guī)律分布，這些網絡中的節(jié)點連接到網路中其他節(jié)點的最短路徑和局部聚類具有共同特性。更確切地說，Barabási和Albert確認了許多社會網絡中節(jié)點連接方式區(qū)別于隨機網絡中節(jié)點的連接方式，即每個節(jié)點的連接數(shù)符合冪律分布。節(jié)點連接的概率P（k）（隨機選定節(jié)點與其他k個節(jié)點相互作用的概率）近似于：

如果一個無向圖節(jié)點度分布服從冪律分布，則表示這個網絡的連通性是無標度的。很多社會現(xiàn)象（social－semiotic phenomena）［28］服從Zipf定律［29］，比如語言單位的頻率分布，它們也因此被稱作無標度網絡（scale－free networks）［21］。無標度意味著沒有代表其他節(jié)點的典型節(jié)點［30－31］。

節(jié)點度的冪律分布可以反映節(jié)點度的“等級”分布（等級由節(jié)點連通性降序決定），也可以反映節(jié)點度的“大小”分布（從2度的節(jié)點到網絡中最高度的節(jié)點的數(shù)量排序），還可以描述有向圖節(jié)點出入度的分布。度分布的冪律說明大部分節(jié)點是不連接的，僅有少數(shù)具有高連接性的中樞節(jié)點（hubs）［32］。這些中心節(jié)點主要任務是提供結合能力，它們把多數(shù)節(jié)點整合到網絡中［33］。因此，對于固定數(shù)量的連接來說，冪指數(shù)越小，曲線的斜面越窄，存在高連接的中樞節(jié)點的概率越高。相比之下，如果一定度的節(jié)點數(shù)量隨著度增長呈指數(shù)衰退，高連接節(jié)點可能會逐漸靠不住或消失。

為了構建一個能夠解釋冪律涌現(xiàn)（emergence）的模型，Barabási和Albert不再考察節(jié)點數(shù)，而是統(tǒng)一考察概率。Barabási和Albert的基本思想是：無標度分布的結果是網絡增長擇優(yōu)行為導致的。動態(tài)網絡中的節(jié)點集合通過連接到高連接的節(jié)點實現(xiàn)增長。這種“擇優(yōu)”行為也被稱作馬太效應（Matthew effect）［34］，它表示已有節(jié)點通過連接新節(jié)點實現(xiàn)“富有”［32］。文獻引用就是一個“富有”的例子，新文獻往往趨向于連接高頻引用的文獻。用公式表示為：假設有概率P（kv），它表示新節(jié)點將要連接到連通性為kv的節(jié)點v上的概率，則存在kv的函數(shù)如式（8）所示，w表示已經連接到網絡的節(jié)點。

在一些試驗中，Barabási和Albert［21］展示了一些根據(jù)此模型演變的網絡發(fā)展為“標度不變”，其中的節(jié)點度分布符合冪律分布（冪指數(shù)通常為2.9± 0.1）。需要注意的是，按照無標度模型產生的網絡并不一定是小世界模型。

盡管無標度模型克服了小世界模型靜態(tài)表述，但無標度模型也忽略了網絡動態(tài)增長的其他因素。比如，網絡可能通過節(jié)點新增和消亡的一定比例實現(xiàn)增長，或者是有些高度節(jié)點不一定直接連接到網絡新節(jié)點。但是無論如何，無標度網絡模型促進了對于網絡及特征進一步的研究，它從純粹隨機網絡中更精確的分離了復雜網絡特征。在語言網絡研究中，劉海濤［5－6，8，24］對漢語依存句法網絡、語義網絡的無標度特性進行了測定，結果顯示它們的節(jié)點度分布均服從冪律分布，冪指數(shù)在2.18～2.439之間。漢語句法、語義、同現(xiàn)詞網絡均符合復雜網絡小世界和無標度特征。小世界、無標度模型的出現(xiàn)成為復雜網絡研究的里程碑。但是我們不難想象，以語言網絡為代表的各類復雜網絡仍可能包含了更多具有特殊性的拓撲結構特點和演化規(guī)律，值得更深入的研究。而網絡的相關性匹配和社團結構特征的發(fā)現(xiàn)，可以稱為社會網絡特殊性研究的最好例證。

5 相關性匹配

在演化網絡中，由于網絡下一步的演化依賴于當前每一個節(jié)點的度，因此新、舊節(jié)點度之間存在相關性。Newman［35－36］提出一個模型，其基本假設就是：兩個節(jié)點連接的概率依賴于這兩個節(jié)點的連通性（connectivity），連通性即節(jié)點度。這個模型用來統(tǒng)計社會網絡中節(jié)點傾向于和有相似特征的節(jié)點發(fā)生連接的程度，這種網絡演化的趨勢叫做節(jié)點的正相關性匹配（assortative mixing）。根據(jù)Newman和Park［37］的研究，這個標準可以區(qū)分都同屬于小世界模型中的社會網絡（如人工網絡）和非社會網絡（如生物、技術網絡）。社會事件節(jié)點相互連接多為正相關連接；技術網絡（如因特網）節(jié)點相互連接多為負相關匹配（disassortative mixing）。Newman始創(chuàng)相關系數(shù)（correlation coefficient）來測量無向網的節(jié)點的連接情況，如式（9）所示。

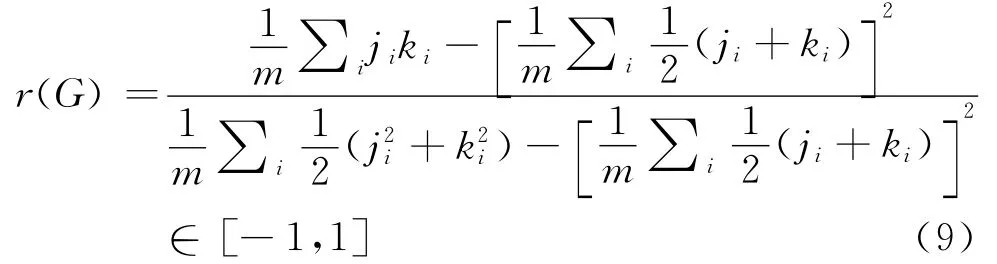
i表示以節(jié)點j、k為頂點的邊，ji和ki表示節(jié)點j、k的節(jié)點度，m＝｜E｜，G＝（V，E）。正相關連接發(fā)生條件是r（G）?0，相反r（G）?0的情況為負相關匹配。劉海濤利用相關系數(shù)對語義網和句法網節(jié)點連接情況進行測量，結果表明漢語的句法、語義網和大多數(shù)生物網絡、技術網絡一樣均為負相關的網絡。但其更有益的發(fā)現(xiàn)在于：語義網相關系數(shù)顯示出弱于句法網的特點。據(jù)此，劉海濤認為句法網絡中虛詞的存在和句法連接增強了語言網絡的相關性，而語義網因為缺少虛詞導致其相關性差是可以被合理解釋的［8］。

盡管相關系數(shù)從復雜網絡中區(qū)分了社會網絡，但它仍不能解釋復雜網絡節(jié)點相關匹配的涌現(xiàn)（emergence of mixing）。因為所有系數(shù)僅僅停留于圖指數(shù)的表示，復雜網絡更高層的結構次序被忽視。為了彌補對網絡結構層次忽視，Newman和Park［37］又提出一個觀點，即社團結構（community structure）。

6 社團結構和模體

社團結構源于社會網絡中成員相互影響的概率依賴于社團（如家庭，聯(lián)盟等）和前后關系（contexts）。這個關系通常是分享性的［32］。共享社團或前后成員關系建立了相互影響的概率。這意味著，一個行動者（agents）進入一個社會網絡并不一定具有與網絡高連接成員接觸的互動機會，這和無標度網絡的節(jié)點增加方式剛好相反。所以社團構建模型并不適合來考量網絡連接上的無標度層級限制。但是Newman［35］利用社團結構模型來研究從屬網絡（affiliation networks）。從屬網絡的最佳實例是科學家合作網，其中同一個社團或前后關系被定義為合作者。從屬網絡是雙向圖建模，節(jié)點行動者（actor）是連接到社團中的行動元。雙向模型轉換為不可分圖（unipartite graph），圖中節(jié)點表示至少被連接到一個社團的行動者。不可分圖被輸入來計算聚集度和平均路徑。Newman［35］的討論核心是相比于隨機圖（Erd?s－Rényi model），這種從屬網絡中聚類是更高級的，原因是社團成員數(shù)量越多，網絡中會存在更多的三角關系。相互作用的節(jié)點a、w也和同社團節(jié)點v相連。社團結構的另一個發(fā)現(xiàn)是節(jié)點的正相關連接可以出現(xiàn)在具有社團結構的網絡中，也會出現(xiàn)在沒有社團結構的社會網絡中。因此網絡的社團結構可以代替節(jié)點連接相關系數(shù)成為更精確的判斷網絡類型的標準。

與社團結構相似的另一個反映網絡局部形式的概念是再生子網絡（recurrent sub－networks）［27，38］。再生子網絡的研究發(fā)現(xiàn)，圖G的子圖G′相比于相同邊數(shù)和節(jié)點的隨機網絡，能夠表現(xiàn)出超預期的特征。這類子圖被稱為模體（Motif）。不同網絡的模體反映網絡的局部連接模式，復雜網絡模體表示的子網絡數(shù)量明顯高于隨機形成的網絡。特定的幾個模體聚集在一起可以形成大的模體簇，這有助于理解網絡的增長機制［39］。模體可以很好地區(qū)分生物網絡、技術網絡和信息網絡。Ravasz et al［33］展示了一個包含模體結構的無標度分布模型，發(fā)現(xiàn)該類模型有內在的等級結構，節(jié)點圍繞高聚集度的節(jié)點構建網絡，而越來越多的節(jié)點逐漸減小聚集度形成外圍的連接。所以此類模型表現(xiàn)出明顯的網絡層級性（hi－erarchical networks），可用于區(qū)分無標度網絡中的層級網絡和非層級網絡。Ravasz et al觀察到該層級網絡模型的節(jié)點度k和聚集系數(shù)C的函數(shù)C（k）隨著節(jié)點度k冪律衰減，表示如下：

這一模型把復雜網絡模體測量簡化為節(jié)點度與聚集系數(shù)的冪律測定。符合該模型的層級網絡更具中心模塊性，作為應用于語言網絡層級性測定的一個模塊化的模型，F(xiàn)errer i Cancho et al［3］測得句法網絡的θ≈1，因為句法網絡來源于層級結構的句法樹所以也具有明顯的層級性。劉海濤［8］對漢語語義網絡的C（k）測定顯示其不服從冪律分布。由此可見，就漢語句法網與語義網的比較，漢語虛詞在語言網絡的節(jié)點負相關匹配和網絡層級性中都扮演重要的角色。

7 以時間為變量的網絡演化

目前除了BA模型關注網絡增長外，幾乎所有的網絡特征都集中反映一定時間點上的網絡靜態(tài)圖。BA模型源于“假設有一個節(jié)點集合，它隨時間演化，表現(xiàn)為不斷有一定節(jié)點度的一定數(shù)量的節(jié)點連接到該集合中”的推導［24］。盡管這個隨時間增長的優(yōu)先連接模型可以表示為當前網絡的度分布指標。但仍有脫離了最初的網絡隨時間演化的實證研究的嫌疑。Leskovec et al［40］通過實證研究把網絡隨時間變化成為網絡的“稠化和收縮”（densification and shrinking）。他們首先觀察到復雜網絡，以文獻引用網為例，隨時間變化越來越密集，這意味著節(jié)點的平均度在隨時間增長。Leskovec et al得到了此類網絡以進程指數(shù)1＜α＜2正相關于時間的冪律分布。其中，e（t）是時間為t時邊的數(shù)量，n（t）表示時間t的節(jié)點數(shù)量。

接著，他們還發(fā)現(xiàn)有效直徑（effective diameter）隨時間縮減。有效直徑表示為網絡中相連節(jié)點間距離的累積分布。實際上網絡增長過程中可能只具備上述特征之一，但研究經驗顯示有必要將其分開考察。需要指出的是Leskovec的網絡依賴時間模型的演變并非要求網絡屬于小世界模型的前提，這為重新考慮和進一步發(fā)展復雜網絡中依賴時間的模型（time－dependent models）提供了參考。目前依賴時間的模型可利用于研究網絡文件的變化，例如，研究維基網站中文本節(jié)點和鏈接變化。這種網絡時間歷時演變的考察方法也是復雜文本網絡的語料庫語言學分析的現(xiàn)實做法。

前面六小節(jié)討論了從復雜網絡的靜態(tài)特征小世界模型到網絡動態(tài)增長的無標度模型，從網絡增長中節(jié)點連接的相關性到比節(jié)點更高層次的網絡模體和社團結構，最后談到網絡演化的時間模型。這一個個模型漸進地限制了不同類復雜網絡的節(jié)點連通性和網絡結構形式，目的都是為了層層剝離出隱藏在系統(tǒng)復雜性背后的形成機制和演化規(guī)律。當今復雜性科學的研究也不再滿足于把復雜網絡簡單描述為“一個由較短的平均路徑，較高的聚集系數(shù)，度分布符合冪律的多節(jié)點網絡”［7］，而是要發(fā)現(xiàn)更有效的適合大規(guī)模節(jié)點的網絡模型［26，41］來預測社會網絡、生物網絡、技術網絡和語言網絡的行為，同時也要發(fā)現(xiàn)更多的具有特殊性的模型來區(qū)別廣泛的復雜系統(tǒng)類型。這一目的也將是語言網絡研究的任務。語言網絡研究是否能像語言計量研究發(fā)現(xiàn)齊夫定律一樣，從語言網絡中探索出普適的規(guī)律和模型來輔助復雜網絡分析。在網絡結構這一共同的基礎上，語言網絡的分析是否能為計算機模擬大腦語言能力提供更可行的和可靠的依據(jù)？這些問題是我們研究的目標也是動力。

［1］ 趙懌怡，劉海濤.基于網絡觀的語言研究［J］.廈門大學學報（哲學社會科學版），2014，226（6）：127－136.

［2］ Sigman M and Cecchi G A.Global organization of the Wordnet lexicon［M］.Procs.Natl.Acad.Sci.USA，2002，99（3）：1742－1747.

［3］ Ferrer i Cancho R，SoléR V，K?hler R.Patterns in syntactic dependency networks［J］.Physical Review E，2004，69（5）：343－358.

［4］ 劉知遠，孫茂松.漢語詞同現(xiàn)網絡的小世界效應和無標度特性［J］.中文信息學報，2007，21（6）：52－58.

［5］ Liu H.The complexity of Chinese dependency syntactic networks［J］.Physica A.，2008，387（12）：3048－3058.

［6］ Liu H.Statistical Properties of Chinese Semantic Networks［J］.Chinese Science Bulletin.2009，54（16）：2781－2785.

［7］ Steyvers M，Tenenbaum J B.The large－scale structure of semantic networks：statistical analyses and a model of semantic growth［J］.Cognitive Science，2005，29（1）：41－78.

［8］ 劉海濤.漢語語義網絡的統(tǒng)計特征［J］.科學通報，2009，54（14）：2060－2064.

［9］ Cong J，Liu H.Approaching human language with complex networks［J］.Physics of Life Reviews，2014，（4）：598－618.

［10］ Zhao Y.Three lines to view language network：Comment on“Approaching human language with complex networks”by Cong and Liu［J］.Physics of Life Reviews，2014，（4）：637－638.

［11］ 趙懌怡，劉海濤.歧義結構理解中依存距離最小化傾向［J］.計算機工程與應用，2014，50（6）：7－11.

［12］ Mehler A.Large Text Networks as an Object of Corpus Linguistic Studies［A］.In：Lüdeling，A.and Kyt?，M.eds.Corpus Linguistics.An International Handbook.Berlin：Walter de Gruyter，2008：328－382.

［13］ Diestel R.Graph Theory［M］.Springer，Heidelberg，2005.

［14］ Melnikov O，Sarvanov V，Tyshkevich R，et al.Exercises in Graph Theory［M］.Kluwer，Dordrecht，1998.

［15］ 趙懌怡，劉海濤語言同現(xiàn)網、句法網、語義網的構建與比較［J］.中文信息學報，2014，28（5）：24－31.

［16］ Otte E，Rousseau R.Social Network Analysis：a Powerful Strategy，Also for the Information Sciences［J］.Journal of Information Science，2002，28（6），443－455.

［17］ Egghe L，Rousseau R.A measure for the cohesion of weighted networks［J］.Journal of the American Society for Information Science，2003，53（3）：193－202.

［18］ Solomonoff R，Rapoport A.Connectivity of random nets［J］.The bulletin of mathematical biophysics，1951，13（2）：107－117.

［19］ Erd?s Rényi.On the Evolution of Random Graphs［J］.Bulletin of the Institute of International Statistics，1961，38（4）：17－61.

［20］ Watts D J，Strogatz S H.Collective dynamic of small－world networks［J］.Nature，1998，393（6684）：440－442.

［21］ Barabási A－L，Albert R.Emergence of scaling in random networks［J］.Science，1999，286（5439）：509－512.

［22］ Milgram S.The small－world problem［J］.Psychology Today，1967，32（2）：185－195.

［23］ Wasserman S，F(xiàn)aust K.Social Network Analysis.Methods and Applications［M］.Cambridge：Cambridge University Press，1999.

［24］ Bollobós B，Riordan O M.Mathematical results on scale－free random graphs［A］.In Bornholdt S and Schuster H G，editors.Handbook of Graphs and Networks.From the Genome to the Internet.Berlin：Wiley－VCH，2003：1－34.

［25］ 劉海濤.漢語句法網絡的復雜性研究［J］.復雜系統(tǒng)與復雜性科學，2007，4（4）：38－44.

［26］ Newman M E J.The structure and function of complex networks［J］.SIAM Review，2003，45（2）：167－256.

［27］ Milo R，Shen－Orr S，Itzkovitz S，et al.Network motifs：simple building blocks of complex networks［J］.Science，2002，298（5594）：824－827.

［28］ Rapoport A.Zipfs law re－visited［A］.In Guiter H and Arapov M V，editors.Studies on Zipfs Law.Bochum：Brockmeyer，1982：1－28.

［29］ Zipf G K.Human Behavior and the Principle of Least Effort：Human Ecology［M］.Massachusetts：Addison－Wesley Press，1949.

［30］ Barabási A－L，Oltvai Z N.Network biology：Understanding the cells functional organization［J］.Nature Reviews.Genetics，2004，5（2）：101－113.

［31］ Newman M E J.Power laws，Pareto distributions and Zipfs law［J］.Contemporary Physics，2004，46（5）：323－351.

［32］ Watts D J.Six Degrees.The Science of a Connected Age［M］.New York／London：W.W.Norton Company，2003.

［33］ Ravasz E，Somera A L，Mongru D A，et al.Hierarchical organization of modularity in metabolic networks［J］.Science，2002，297（5586）：1551－1555.

［34］ Simon H A.On a class of skew distribution functions［J］.Biometrika，1955：42：425－440.

［35］ Newman，M.E.J.Assortative mixing in networks［J］.Physical Review Letters，2002，89（20）：208701.

［36］ Newman M E J.Mixing patterns in networks［J］.Physical Review E，2003，67（2）：241－251.

［37］ Newman M E J，Park J.Why social networks are different from other types of networks［J］.Physical Review E，2003，68（3）：036122.

［38］ Itzkovitz S，Milo R，Kashtan N，et al.Subgraphs in random networks［J］.Physical Review E，2003，68（2）：125－149.

［39］ Motter A E，De M A Lai，Y C，et al.Topology of the conceptual network of language［J］.Physical Review E.2002，65（6）：065102.

［40］ Leskovec J，Kleinberg J，F(xiàn)aloutsos C.Graphs over time：densification laws，shrinking diameters and possible explanations［A］.In KDD 05：Proceeding of the eleventh ACM SIGKDD international conference on Knowledge discovery in data mining.New York：ACM Press，2005：177－187.

［41］ Bornholdt S，Schuster H G.Handbook of Graphs and Networks.From the Genome to the Internet［M］.Weinheim：Wiley－VCH，2003.