基于ANSYS/LS-DYNA 的高強度鋼絲縮徑旋壓過程應力應變分析

張 瑋，盧秀春，劉 金

(燕山大學 機械工程學院，河北 秦皇島 066004)

0 前言

高強度鋼絲是一種技術含量很高的預應力鋼材，在國內外已被廣泛應用于凝土離心管樁、高架橋墩、高速鐵路軌枕板等預應力構件中［1］。目前對鋼絲兩端外圓的加工所采用的方法是滾鍛加工或切削加工，這種方法消耗人力和資源，噪聲大，加工過程中的振動對人體有一定損傷。旋壓技術作為一種先進的塑性成形工藝，適用于高強度、難變形的材料的加工［2－3］，但其在小直徑實心軸類件上的研究較少，本文采用計算機數值模擬的方法，結合旋壓工藝對鋼絲外圓縮徑過程進行研究，描述成形過程中應力、應變分布規律，分析縮徑成形的變形機理，為鋼絲外圓旋壓加工提供了新的方法和參考依據。

1 有限元模型的建立

為了簡化計算和提高計算效率，只對鋼絲長度的一部分進行建模，針對實際工況的復雜性和有限元模擬的局限性，做出如下假設:

1)鋼絲采用光圓鋼絲模型，且材質均勻，各向同性且不可壓縮。

2)模擬計算時，忽略慣性力的影響和摩擦引起的溫度的影響。

鋼絲的主要材料參數如表1 所示。

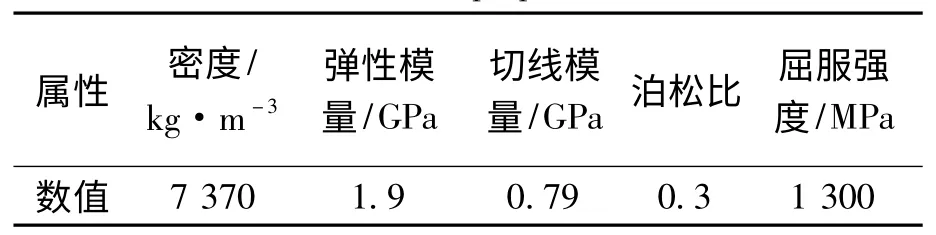
表1 鋼絲的主要材料參數Tab.1 Main material properties of steel wire

鋼絲直徑為10.5 mm，轉速為240 r/min，大旋輪直徑為140 mm，小旋輪直徑為40 mm，大旋輪與小旋輪的圓角半徑都為8 mm，成形角都為25 ℃，進給比為0.5 mm/r，三旋輪中心相對鋼絲中心呈122°和116°分布方式，三維模型如圖1 所示。

鋼絲將采用雙線性強化模型，并用solid 164單元進行網格劃分，端面網格尺寸設置為0.5 mm，軸向網格尺寸設置為0.3 mm，旋輪采用剛體模型，并用shell163 單元進行網格劃分，網格尺寸設置為1 mm;接觸設置將采用自動單面接觸，設定旋輪為目標面，鋼絲表面為接觸面［4］;模擬時鋼絲設定為固定，旋輪繞鋼絲的中心軸轉動的同時沿著軸向進給運動，旋輪與鋼絲之間摩擦采用常摩擦系數法，設定庫倫摩擦系數均為0.1，為了避免模擬時產生振蕩，導致計算終止，設置阻尼系數為20。

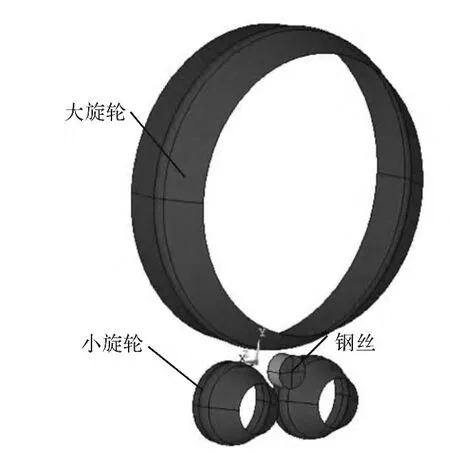
圖1 實體模型Fig.1 Solid model

2 應力應變分析

圖2為旋輪軸向進給4 mm 時鋼絲的三向主應力分布圖，由應力值和分布情況可以看出:旋輪與鋼絲接觸區的金屬三向應力狀態都為壓應力狀態，且接觸區域金屬所受到的壓應力數值最大;第一主應力方向上，旋輪進給方向未接觸的金屬區域表面受到拉應力，進給方向相反的未接觸金屬區域表面受到壓應力;第三主應力方向上，旋輪進給方向未接觸的金屬區域表面受到拉應力，其余的金屬區域表面受到壓應力作用;第二主應力方向上的分布情況與第一主應力方向分布相同。

圖2 三向主應力分布Fig.2 Distribution of the three principal stress

圖3 是旋輪軸向進給4 mm 時，鋼絲在三維笛卡爾直角坐標系下三個方向上的應變分布，由圖可以看出旋輪與鋼絲接觸區的金屬在徑向與切向方向上受到壓應變，處于壓縮變形，軸向受到拉應變處于伸長變形。在非接觸區旋輪進給方向金屬徑向和切向受拉應變處于伸長變形，軸向受壓應變，隨著縮徑過程的進行會造成旋輪前方金屬的堆積隆起，后方金屬受拉應變，拉應變的數值大于壓應變，導致縮徑過程中軸向伸長變形。

圖4為旋輪與鋼絲接觸區橫截面的三向應力分布圖，從圖中可以看出變形區域不僅限于鋼絲的表面，鋼絲的內部也有應力變化。x、y 方向上，旋輪壓下形成的壓應力區域越往鋼絲內部值越小，鋼絲內其他區域受到拉應力;軸向應力分布比較規則，其中旋輪之間區域表面受到拉應力作用，旋輪壓下區域軸向受壓，緊接著有一個壓應力環狀區域，與旋輪壓下形成的壓應力區域聯通，再往鋼絲內部有一層拉應力環狀區域，在鋼絲中心處有一小片區域受到壓應力，形成了四個層次分布均勻的環狀區域。

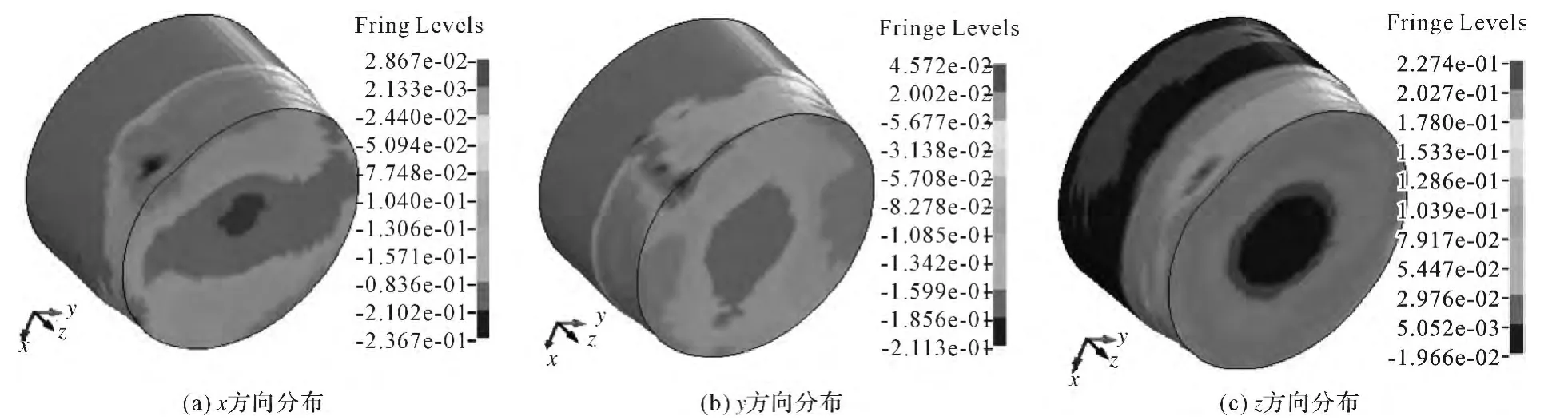
圖3 三向應變分布Fig.3 Distribution of strain in three directions

圖4 接觸區橫截面的應力分布Fig.4 Distribution of the cross section stress in contact zone

圖5為旋輪與鋼絲接觸區橫截面的軸向應變分布圖，由圖中可以看到，軸向應變為拉應變，鋼絲軸向處于伸長變形，旋輪壓下區域的拉應變值較大，越靠近鋼絲中心部，其值越小，不同應變值形成了相應的環狀區域，軸向應變分布跟軸向應力分布相似，比較規律，呈四個環狀區域分布。

圖5 接觸區橫截面軸向應變分布Fig.5 Distribution of the cross section strain along Z direction in contact zone

3 鋼絲表面一單元應力應變分析

截取鋼絲表面距離軸端2 mm 處一單元，查看其在縮徑過程中的等效應力和等效應變分布情況，來反映出成形過程中鋼絲的等效應力應變分布規律，更深入的研究縮徑過程的變形機理。

圖6 是縮徑過程中該單元的等效應力與等效應變隨時間的變化曲線，從圖6a 可以看出，該單元在縮徑過程中等效應力變化范圍比較大，在0.5 s～1 s 內出現了周期性變化，等效應力峰值時刻說明該單元正處在旋輪與鋼絲的接觸區域，應力極小值時刻說明該單元沒有與旋輪接觸。1 s之后等效應力存在，說明旋輪繼續軸向進給，鋼絲軸向伸長，金屬材料軸向流動，單元之間相互擠壓產生應力變化，隨著與旋輪距離的增大，所受到的等效應力值變化較小;從圖6b 中可以看出該單元的等效應變隨時間呈遞增趨勢，從剛開始到1.4 s 金屬的等效應變增大，增長較快，主要由于受旋輪的擠壓變形，1.4 s 之后隨著縮徑過程的進行，等效應變繼續增大，材料流動變形量大，但變化速率逐漸減小，等效應變值趨于不變，成形較為穩定。

4 模型結果可靠性驗證

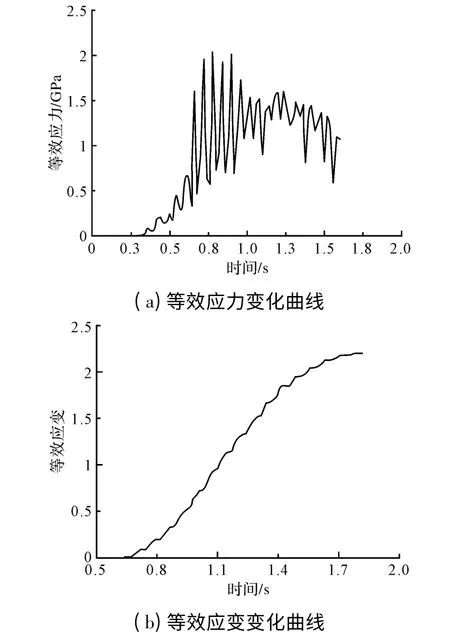
圖6 鋼絲表面一單元的應力應變變化曲線Fig.6 The stress and strain curve of a unit of outer surface

模擬計算過程中采用質量縮放技術可以有效的減少計算時間，但是縮放太大，容易影響計算的精度和收斂性［5］。圖7為鋼絲動能與內能的比值隨時間的變化曲線，從圖中可以看出，動能與內能的比值一直控制在0.025%之內;

另外模擬計算過程中采用Solid 164 單元劃分網格時，容易激起“沙漏”模式，導致計算結果數值的震蕩或者完全失真，圖8 所示為沙漏能與內能的比值隨時間的變化曲線，從圖中可以看出，沙漏能與內能的比值一直控制在2.5% 之內，一般認為在模擬計算過程中鋼絲動能與勢能的比值較小，不超過10%，沙漏能不超過內能的5%～10%，計算結果是有效的［6］。因此本次仿真計算所建立的有限元模型是可靠的，結果是可信的。

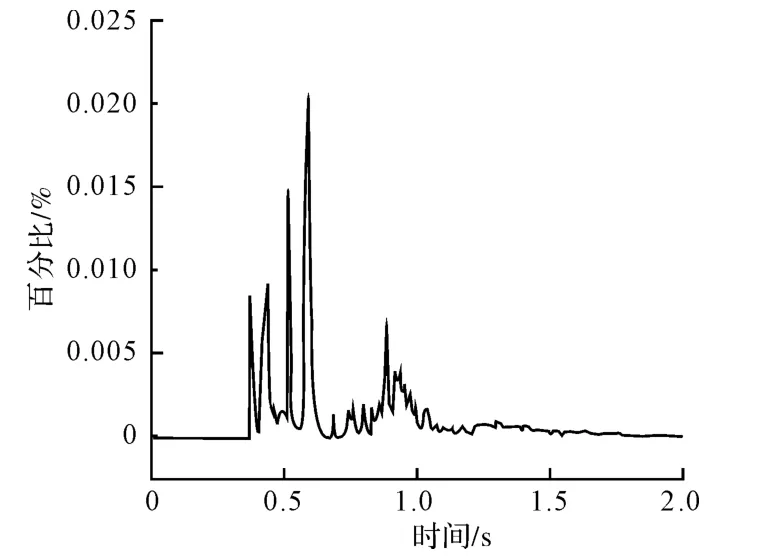
圖7 動能與內能的比值變化曲線Fig.7 Ratio curve of kinetic energy and internal energy

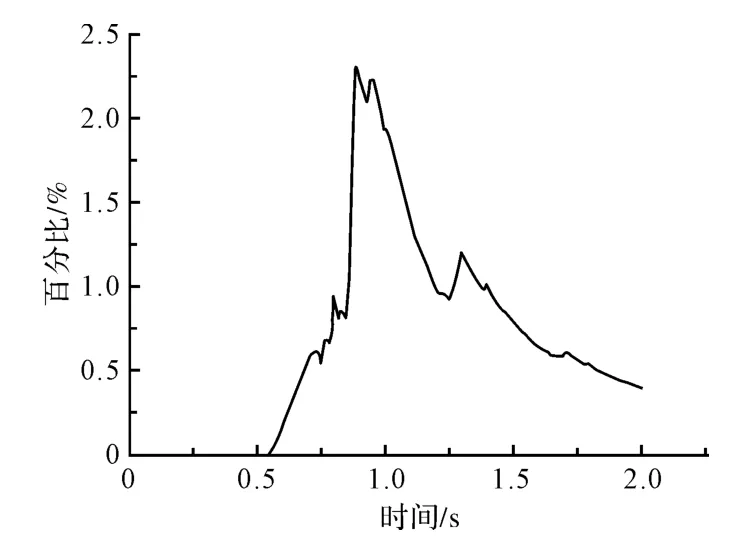
圖8 沙漏能與內能的比值變化曲線Fig.8 Ratio curve of hourglass energy and internal energy

5 結論

(1)應力分布規律。鋼絲與旋輪的接觸區三向應力狀態為壓應力狀態;非接觸區旋輪進給方向反向金屬區域表面受壓應力，進給方向金屬表面區域受拉應力;接觸區橫截面軸向應力分布呈層次分布的環狀，在徑向和切向上，旋輪壓下區域形成壓應力，并越往鋼絲內部值越小，其他區域受到拉應力。

(2)應變分布規律。旋輪與鋼絲接觸區的金屬在徑向與切向方向上受到壓應變，軸向受到拉應變，在非接觸區旋輪進給方向金屬徑向和切向受拉應變，軸向受壓應變，進給方向反向金屬受拉應變;接觸區橫截面軸向受拉應變，并呈分布層次規律的應變環，越往軸中心應變值越小。

(3)鋼絲縮徑成形的變形機理為鋼絲與旋輪接觸區金屬徑向與切向被壓縮，沿軸向流動，隨著旋輪軸向進給，軸向方向離旋輪距離越遠的金屬區域變形量越大，但變形速率越低，成形過程是鋼絲整體參加塑性變形且連續變化的過程。

(4)鋼絲外圓表面所形成的應力狀態符合工程使用要求，對應用旋壓工藝加工小直徑軸類件方面提供了理論參考，同時對鋼絲外圓旋壓加工具有一定的參考價值。

［1］周和敏，左鐵鏞，易長森，等.高強度預應力螺旋肋、螺旋槽鋼絲的研制［J］.北京工業大學學報，2000，26(2):30－34.

［2］趙云豪，李彥利.旋壓技術與應用［M］.北京:機械工業出版社，2008.

［3］張濤 旋壓成形工藝［M］.北京:化學工業出版社，2009.

［4］梅瑛，李瑞琴，張晨愛，等.筒形件強力反旋的數值模擬及旋壓力分析［J］.機械設計與研究，2007，23(4):65－68.

［5］祖汪明，束學道，彭文飛.質量縮放技術在楔橫軋有限元模擬中的應用［J］.冶金設備，2008(3).