基于數據挖掘的電站運行參數目標值優化

王秋平，陳志強，魏 浩

(東北電力大學 自動化學院，吉林吉林132012)

基于數據挖掘的電站運行參數目標值優化

王秋平，陳志強，魏 浩

(東北電力大學 自動化學院，吉林吉林132012)

為提高電站經濟性和機組運行效率，降低機組發電煤耗，求取電站機組運行參數最優值是關鍵技術。以往通過理論計算得到最優運行參數值是在設定的理想環境下得到的，在實際的電站運行過程中難以實現。而數據挖掘算法是從電站自身的歷史數據中得到的最優運行參數值，電站機組能夠很容易在實際運行中實現該值。通過對比近年來電站常用數據挖掘算法，總結出基于數據挖掘的電站優化運行的主要步驟為關聯規則、數據離散化、運行工況劃分、粗糙集知識約減。得出以下結論：模糊關聯規則挖掘算法是電站數據挖掘中的最主要方法，能夠適用于大多數的電站優化目標值挖掘；模糊聚類離散化能夠克服邊界劃分過硬的問題，將電站中的連接參數離散化；粗糙集屬性約減能夠有效降低數據挖掘的參數維度，提高挖掘效率。同時指出基于數據挖掘的電站優化運行算法將成為電站運行參數優化的主要研究方向。

關聯規則；數據離散化；工況劃分；知識約簡

0 引言

為了保證電廠的經濟性，電站機組應盡量維持在最優的工況下運行。然而在實際的運行中，由于外界負荷、煤質以及運行人員的操作等因素常常使得機組偏離最佳工況運行，造成了一定的經濟損失。為了維持機組在較優的狀況下運行，迫切需要針對不同的外界工況挖掘出機組所能達到的最優運行狀態以及最優運行狀態下各個可調參數最優運行范圍，以此來指導電廠的實際運行。目前普遍是采用數據挖掘算法，從電廠海量的歷史數據中挖掘出電站機組在不同的工況條件下達到過的最優值。數據挖掘算法得到的結果雖然可能不是機組理論上的最優值，但卻是機組最容易達到的最優值，比起理論最優值更具有實際意義[1]。在電站的數據挖掘參數最優目標值的過程中，廣泛應用的數據挖掘方法包括關聯規則、數據離散化、工況劃分等。

本文綜述了近年來采用數據挖掘算法確定電站運行參數優化目標值過程中重要步驟所使用的各類方法，如關聯規則、粗糙集約簡、工況劃分、數據離散化、數據預處理等。

1 電站運行參數目標值優化

火電廠運行的經濟性受到多種因素的影響，其中主要有機組負荷、使用的煤質、外界的環境條件以及運行人員的運行操作水平。火電廠運行參數最優目標值反映的是機組不同運行工況條件下，所能達到的最佳運行時的各個可調參數的值，是機組經濟性和優化運行的基礎。

數據挖掘電站優化目標值是從電站海量的歷史運行數據中，通過一定的挖掘算法，挖掘出電站在不同工況下的運行最優值。由于該值是電站的歷史記錄，所以是運行優化最容易實現的，與傳統理論計算方法得到的最優值相比，數據挖掘得到的優化目標值更有實際應用的意義。

目前，通過數據挖掘算法來獲取電廠優化目標值的基本流程步驟如圖1。

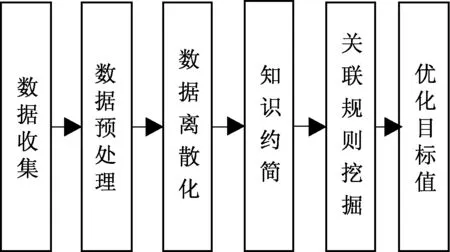
圖1 優化目標值獲取流程

2 關聯規則在電站優化中的應用

關聯規則挖掘算法[2]是電站優化目標值挖掘的基礎，但傳統的關聯規則并不能直接應用在電站中，需要對傳統關聯算法進行改進，常見的應用在電站優化目標值挖掘的改進關聯算法如下所述。

2.1 量化關聯規則數據挖掘在優化中的應用

Apriori關聯規則是最經典的數據挖掘算法，最初是用于描述二進制數據的，對于電廠的連續數據無法適用，因此研究人員提出了量化關聯規則算法。

量化關聯規則是將連續型數據進行區間劃分，即將需要量化的數據劃分成不同小區間，每個區間用一個不同符號表示，連續數據屬于劃分的區間內表示為1，否則為0。這樣將連續數據離散化為布爾型數據。然后，再采用布爾型關聯規則挖掘算法尋找量化規則。量化關聯規則簡單易于理解應用，能夠將電站中的連續運行參數通過簡單的區間劃分轉換為一個個離散的二進制數據，再利用成熟的Apriori算法，實現電站對連續型參數的數據挖掘。

2.2 模糊量化關聯規則在優化中應用

量化關聯規則中的數據離散化直接將屬于某一個區間內的數據完全劃分到該區間內，得到的離散化數據有兩個缺點：(1)劃分區間的邊界過硬；(2)處理具有較高偏度的數據時很難體現出數據的實際分布狀況，在劃分邊界處得到的關聯規則不夠準確。模糊關聯規則的挖掘方法能夠解決這兩個問題。

模糊關聯規則挖掘算法，是將Apriori算法擴展到模糊屬性事務中，用模糊集將各個劃分好的屬性區間進行模糊離散化，得到離散化的數據[3]。模糊離散化中利用邊界交織在一起的隸屬度函數求取各個連續模糊區間的隸屬度值。用隸屬度的權值w來代替Apriori的頻繁項集的支持度s。之后采用與Apriori類似的算法，刪除小于minSup和minConf的項，得到滿足最小支持度和最小可信度的關聯規則。其中的歸一化處理為公式(1)；模糊化處理為公式(2)；權值求取為公式(3)。

(1)

式中：v(i)為記錄中的各個真實值。

(2)

式中：Rjk為項目tij的第k個模糊區分；ui(Rjk)為分區Rjk上的隸屬度值。

隸屬度的權值：

(3)

模糊關聯規則解決了數量型關聯規則邊界過硬和數據偏差大的問題，同時拓寬了傳統確定性關聯規則的表示應用的方法。利用模糊關聯規則表示屬性間的關系，更符合人的思維習慣和推理方式，目前模糊關聯規則挖掘常常應用在鍋爐運行時過量空氣系數、排煙溫度、排煙氧量等參數的確定。

2.3 增量數據挖掘在運行優化中的應用

實際運行的電廠數據庫并不是靜態的。當數據庫發生變化時，已經挖掘出的規則可能不再適用，因此關聯規則需要經常進行維護。采用重新挖掘的維護方式費時費力，因此有學者提出增量式挖掘算法實現更新和原有挖掘規則的維護。針對電站連續數據，牛成林在模糊量化關聯規則關聯規則的基礎上提出了改進的增量式模糊數值型關聯規則挖掘算法[4]。

增量式數據挖掘運行優化目標值的基本方法為：首先將數據歸一化和模糊離散化，然后計算各個模糊集合的權值，接著利用增量數據挖掘的性質：頻繁項的子集也是頻繁的；不頻繁項的超集也是不頻繁的挖掘更新后的頻繁項集，最后再通過頻繁項集構造關聯規則，得到更新數據庫后的新的關聯規則，其中利用性質更新關聯規則是增量挖掘的新穎之處。

增量式關聯規則挖掘充分利用原有的挖掘結果，能夠避免重復挖掘，提高挖掘效率,常應用在電站氧量最優值的確定上[5]。

2.4 基于動態數據流在優化中應用

增量數據挖掘技術進行挖掘解決了數據庫更新后運行優化目標值的增量更新問題。但機組的實際運行的狀態與歷史數據得來的目標值仍有時間延遲，運行優化目標值無法實現實時更新。基于動態數據的運行優化方法能應對此類問題。

動態數據挖掘的基本思想是：將數據流分割成若干個固定大小的批，計算出每批數據集中各個項的支持度技術，然后采用類似FP-Stream算法加入大于最小支持度和最小可信度的各個項，對FP-stream進行更新。

動態數據挖掘的方法通過加大增量挖掘的頻度，解決了挖掘結果與實際運行結果有“時間差”導致的挖掘出的結果偏離當前狀態“較遠”，挖掘結果不可用的問題。與傳統的基于靜態歷史數據的增量數據挖掘方法相比，該方法在時間響應上更具有優勢，目前用該方法研究電站最經濟煤種決策[6]。

3 電站關聯規則應用的優化技術

關聯規則是電站優化目標值確定最為基本的理論，但僅依靠關聯規則無法充分挖掘出優化目標值，因此，需要其他理論方法為關聯規則的使用提供支持。其中主要包括數據預處理、數據離散化、工況劃分、知識約簡等重要步驟。

3.1 數據預處理

數據收集是針對不同的優化目標，從DCS中選取出對優化目標有影響的各個參數的歷史數據。參數的選取可以通過對鍋爐的熱平衡公式進行確定。如優化目標是鍋爐的燃燒效率，此時就可以選擇過量空氣系數、風煤比、外界負荷、排煙溫度等參數作為需要收集的數據。

由于電站現場有電磁干擾、設備或傳感器故障等原因，電站記錄的真實數據包含有許多噪聲、空缺、奇異等數據，使數據挖掘挖掘過程中面對大量的不統一和存在錯誤的數據，因此，數據預處理是數據挖掘中必備可少的步驟。數據預處理的過程主要包括數據清理、數據轉換、數據規約[6，7]。

3.2 數據離散化

電廠中的參數大多是連續的數值型數據，對數值型數據進行關聯挖掘，需要先將連續數值轉換為離散值，再用類似布爾型關聯規則進行挖掘[8]。目前電站常用離散化方法主要有等寬度法、等頻率法和聚類算法等。

(1)等寬度劃分離散化。等寬度法將屬性的值域劃分成具有相同寬度的區間，使得每個區間大致包含相同數目的樣本，然后用一個符號來表示這段區間(常用區間中心值)。離散區間的個數k由用戶指定，由于區間大小對后期使用關聯規則挖掘結果影響很大，一般要求離散化區間不能過大或過小，且要有較好的離散化效果。區間劃分必須在挖掘過程中不斷摸索改進[9]。

等寬度離散化算法簡單，占用時間少，可以依據經驗人為設定離散區間[10]。但對于區間存在偏斜極為嚴重的點非常不準確。

(2)等頻率離散化。等頻區間離散化法與等寬度離散化方法類似，也是將數值屬性的值域劃分為K個小區間，不同的是等頻區間法要求每個區間的樣本數目相等[11]，其性能和特點也和等寬度離散化相類似。

(3)K-means聚類離散化。K-means聚類是一種基于劃分的聚類算法，簡單地將數據對象劃分成不重疊的子集，使得每個數據對象恰好在一個子集中。每個簇的平均值代表這一段數據，以此將這一段數據離散化。

對于電站的大數據集，如果數據是分布較為均勻的，這樣劃分的結果簇是密集的，且簇與簇之間的劃分是明顯的。K-means算法具有相對可伸縮性和高效性，常應用在機組負荷和煤質的自然工況劃分上。

(4)模糊聚類離散化。以上的劃分都是一種硬劃分，將某個對象嚴格劃分到某個類中，具有非此即彼的性質。然而對于實際的電站運行參數，它們的數值并沒有嚴格的類劃分，在類屬性的方面具有亦此亦彼的中介性，研究人員引入模糊集理論來解決劃分過硬的問題。

電廠模糊離散化中，最為常用的方法是模糊C均值聚類算法(FCM, Fuzzy C-Means)。該算法中，各個樣本不是被唯一的劃分到某一類中，而是以不同的隸屬度劃分到各個類別，將各個類的隸屬度擴展到[0,1]，用[0,1]中的數值表示該記錄屬于不同的類，有效解決了數據劃分過硬的問題。

3.3 工況劃分

火電機組運行效率會受到許多外界條件影響，這些外界條件人為難以改變，稱之為工況。工況的變動會造成機組運行參數和相應指標的變動。火電機組在不同工況下運行特性差異性很大，對應的最優值也是不同的[12]。因此，數據挖掘電站優化目標值之前需要對機組運行工況進行劃分，目前工況具有以下幾種劃分方法。

(1)單一外界負荷工況的劃分。電站機組的設計一般都是根據額定負荷進行的，因此機組在額定負荷下經濟性最好。負荷的變化會引起許多運行參數偏離基準值，引起機組相應性能的變化[13]。因此，負荷作為工況的劃分的方法是選擇機組比較常見典型負荷作為機組的工況劃分,如將50%，80%，90%，100%等負荷劃分為獨立工況。

(2)多外界條件的人工劃分。外界負荷并不是唯一的影響機組運行效率的不可控條件，煤質和外界環境溫度對機組的運行效率也是十分重要的外界因素。于是研究人員使用等寬度法將煤質系數[14]、外界環境溫度、負荷分別進行均勻的區間劃分。各個劃分后的參數區間組合起來定義為不同的工況，每個工況用一個單獨的符號表示。

(3)多因素自然工況劃分。電廠的典型負荷不一定是其常見的運行工況，煤質用等寬度的方法直接進行劃分也缺乏科學性，因此引入了自然工況劃分方法，采用聚類算法中K-means算法將負荷和煤質進行自然劃分。而對于變化緩慢的外界環境溫度仍采用等寬度法進行劃分。其中K-means算法的公式為：

(4)

式中：E為數據庫中所有對象與相應簇的質心的距離之和；p為對象空間中的一個點；mi為簇的算數平均值。

(4)改進K均值聚類算法的工況劃分。傳統K-means算法需要首先指定構造的簇數K，而沒有可靠方法判斷K值是否選取的正確；K-means同時對初值敏感，初始值選取不當可能使結果陷入局部最優解的缺點。文獻[15]提出了一種采用均值標準差的方法確定初始聚類中心，通過評價函數自適應調整值改進K均值聚類算法，解決了初值敏感問題；文獻[16]提出了一種SOM神經網絡改進K均值算法相結合的雙層聚類算法，利用SOM神經網絡將大量實時數據進行壓縮，再利用改進K均值聚類算法將神經元聚類。SOM神經網絡改進K均值算法改善了K-means的處理離散點時導致的分類增加問題，降低了數據聚類的計算量，從而降低了運算的時間。

總之，單一的負荷劃分簡單、高效，有一定的實際應用依據，但劃分方法太過粗糙，不能夠滿足全工況節能優化運行、AGC約束變化[17]。多因素人工劃分對于工況的劃分更為細致準確，但人為確定負荷和煤質的劃分寬度，缺乏科學依據。自然工況劃分，遵循了機組運行工況的自然分布規律，考慮了不同電廠運行的客觀規律，劃分方法物理意義明確其易于工程實現。改進k-means方法具有更高的分類準確率及更強的無監督自學習能力，能契合實際生產規律。

3.4 屬性約簡

在優化過程中通常會選取一些決策屬性顯示機組的經濟性，如鍋爐效率、發電煤耗等。電站中的許多參數對決策參數都有影響，但每個參數影響程度大小不同，如果把每個有影響的參數都納入到挖掘的對象中，會使得挖掘效率變得極低。因此，需要引入一種方法來降低挖掘的維數。目前應用的較多的屬性約簡方法如下：

(1)粗糙集屬性約簡。粗糙集理論的主要思想是在保持分類能力不變的前提下，通過知識約簡，得到問題的決策或分類規則；而在優化目標值確定的過程中應用粗糙集，是在保持條件屬性相對于決策屬性的分類能力不變的情況下，刪除其中不必要或不重要的屬性[18]。這里主要介紹基于區分矩陣的約簡算法。

區分矩陣[19]由Showron提出。區分矩陣約簡首先構建出一個差別矩陣，然后通過差別矩陣計計算出各個參數集合的區分函數，區分函數值小的集合將會被舍棄掉，最終保留下較少的區分函數大的集合，這些集合就是約簡后的參數集合。

區分矩陣的約簡算法清晰簡單，但對于有較多影響因素的參數集合，該算法的區分函數龐大，計算復雜。對于改進的基于區分矩陣的約簡算法有多種[20]，在這里不再詳述。

(2)基于參數的關聯性分析。火電廠的生產過程實際上是一個能力轉換傳遞的過程，體現了其內在的物質平衡和能量平衡的關系。這個平衡關系使得整個生產過程中許多參數是有相關性的[21]，變量間的相關關系可以用解析式表達出來。描述變量間相關性的指標采用隨機變量的相關系數，變量X、Y的相關系數定義為：

(5)

式中：Cov(X,Y)=E(X-Ex)(Y-Ey)=EXY-EXEY，Var(X)、Var(Y)分別是X、Y的方差。

變量間的相關性可以通過求樣本相關矩陣來估計，文獻[22]給出了相關矩陣行列進行調整以尋找相關數據塊的方法，以此可按照關系數對運行參數重新分組，從而找到具有較強相關性的變量組作為重要的約簡屬性集。

綜述，屬性約簡能夠降低關聯規則挖掘的維數，提高關聯規則挖掘效率。盲目刪除屬性方法直觀簡單、易于理解，但計算過程空間及時間復雜度過高；重要度的約簡過程也計算較慢；區分矩陣和區分函數以及他們的改進版本能夠較好地處理屬性約簡的過程，適合電站數據挖掘過程中的使用。目前，電站應用較廣的是基于粗糙集的屬性約簡算法，在鍋爐效率的影響參數的約簡、發電煤耗影響參數的約簡上得到應用。

4 結論

基于數據挖掘的電站優化運行算法是一種與計算機技術緊密結合的定量的優化運行方法。該方法以電站海量歷史運行數據為基礎，主要應用關聯分析法從歷史數據中挖掘出符合優化目標的參數運行范圍。比傳統的依靠理論計算確定優化目標值更符合電站實際運行狀態；挖掘出的運行參數優化目標值比理論計算法更容易在電站中指導電站運行。因此，隨著計算機技術的不斷發展和SIS系統在電站中的廣泛應用，電站數據挖掘優化算法將能夠不斷從電站海量運行歷史記錄中挖掘出機組在安全、經濟、環保、高效條件下的運行規律，為電站的實時優化運行提供指導。基于數據挖掘的電站優化運行算法將成為電站運行參數優化的重要研究方向。

[1]Zhao W J, Liu C. The Optimizing for Boiler Combustion Based on Fuzzy Association Rules[C].2011 International Conference of Soft Computing and Pattern Recognition, Dalian, China, 14-16 October, 2011.

[2]Liu W C, Shi H J, Ma S Q. Algorithm of Weight Fuzzy Association rules[J].Computer Engineering and Design,2010, 31(16):3654-3657．

[3]Li J Q, Niu C L, Gu J J, et al. Energy Loss Analysis Based on Fuzzy Association Rule Mining in power Plant[C].International Symposium on Computational Intelligence and Design, Wuhan, China, 17-18 October, 2008:186-189.

[4]牛成林．增量數據挖掘及其在電站運行中的理論研究及應用[D]. 北京：華北電力大學，2010.

[5]Niu C J, Li J Q, Liu J Z, et al. The application of improved incremental updating association rule mining in optimal oxygen content[C].International Symposium on Computational Intelligence and Design, Wuhan, China,17 October,2008:246-249.

[6]冉鵬．基于動態數據挖掘的電站熱力系統運行優化方法研究[D].北京：華北電力大學，2012：1-124.

[7]Han J W, Kamber M, Pei J. Data Mining Concepts and Techniques[M]. New York: Margan Kaufmann Publishers,2011.

[8]Li J Q, Niu C L, Liu J Z. Application of Data Mining Technique in Optimizing the Operation of Power Plants [J].Journal of Power Engineering，2006, 26(6):830-835.[9]翟少磊，黃孝彬，劉吉臻．基于工況劃分的電廠經濟性指標挖掘[J].中國電力， 2009，42(7)：68-71.

[10]鄭茜茜，楊海婭，谷俊杰．基于關聯規則的電廠優化目標值確定的研究[J].電力科學與工程， 2010，26(9)：48-51.

[11]張仁杰．粗糙集理論在電站運行優化中的應用研究[D].北京：華北電力大學， 2011：1-44.

[12]李宗山．機組經濟運行模式數據挖掘系統的研究與開發[D].北京：華北電力大學，2011：1-61.

[13]Li J Q,Liu J Z.The research and application of data Mining in power plant operation optimization[C].International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18-21 August, 2005:1642-1647.

[14]趙征，劉吉臻，田亮．基于數據融合的燃料量軟測量及煤質發熱量在線校正[J].熱能動力工程，2007，22(1)：42-45,60.

[15]苑一方，孫建平，田婧．改進K均值聚類算法在電廠工況劃分中的實現[J].儀器儀表用戶，2010，17(4)：54-55.

[16]苑一方，孫建平．基于電廠工況劃分的雙層聚類算法研究[J].電力科學與工程，2010，26(9)：56-58.

[17]楊婷婷．基于數據的電站節能優化控制研究[D].北京：華北電力大學，2010：1-105.

[18]高俊山，郎平，孫真和．基于改進粗糙集方法的電力系統數據挖掘[J].自動化技術與應用，2009，28(3)：15-17.

[19]蘇健．基于粗糙集的數據挖掘與決策支持方法研究[D].杭州：浙江大學，2002：1-121.

[20]陳丹丹．基于粗糙集的電站運行數據分析與運行優化[D].保定：華北電力大學，2013：1-60.

[21]Li J Q，Niu C L, Liu J Z, et al. TanWen.Correlation Analysis of Operation Data and Its Application in Operation in Power plant[C].Fifth International Conference on Fuzzy Systems and Knowledge Discovery,Shandong, China, 18-20 October, 2008:581-585.

[22]李建強．基于數據挖掘的電站運行優化理論研究與應用[D]保定：華北電力大學，2006：1-119.

The Summary of Optimal Operation Parameters in Power Station Based on the Data Mining

Wang Qiuping, Chen Zhiqiang, Wei Hao

(Department of Automation,Northeast Dianli University, Jilin 132012, China)

In order to increase the economy and the operation efficiency of the power plant and decrease the coal consumption of electrical facilities, it is of great significance to get the optimal operation parameter value of power station. The previous optimal operating parameters were obtained by theortical calculation under the ideal environment, which were difficult to achieve in the actual operation of the power plant. However, the data mining algorithm is a way to get the optimal operating parameters from previous data, which can easily obtained in the actual operation. By comparing previous data mining algorithm of power plant in recent years, the paper summarized the main steps of optimal parameters by data mining, which include association rules, data discretization, condition identification and knowledge reduction. In addition, it concluded that fuzzy association data mining is the main method of data mining in power plant, which can be applied to power stations for optimization value mining and fuzzy clustering discretization can disperse the continuous data of parameters in power plant. Rough set theory can reduce the dimension of parameters and improve the efficiency of data mining. Finally, the result shows the optimization of parameter based on data mining algorithm may provide guidence for optimal running future research.

association rules; data discretization; condition identification; knowledge reduction

2015-05-04。

王秋平(1973-)，女，副教授，研究領域為卡爾曼濾波、火電機組數據挖掘，E-mail:18654929296@163.com。

TP274.2

A

10.3969/j.issn.1672-0792.2015.07.004