風力發電系統可靠性建模與優化檢修策略

秦 洋，馬慧民，朱田瑋,朱慶華

(上海電機學院 電氣學院， 上海200240)

風力發電系統可靠性建模與優化檢修策略

秦 洋，馬慧民，朱田瑋,朱慶華

(上海電機學院 電氣學院， 上海200240)

針對風力發電系統可靠性評估及運行維護存在的問題，對雙饋風力發電系統的運行原理、故障機制進行了研究，運用馬爾可夫過程方法和可靠性理論建立了風力發電系統的可靠性模型，在考慮系統隨機故障和老化故障的情況下，提出了一種改進型發電系統的狀態檢修模型，根據系統的狀態轉移關系得到系統的狀態轉移矩陣，借助MATLAB對系統的可用度進行求解并探討了檢測時間對于系統可用度的影響，最后分析得出不同發電老化系統可靠性最優時的檢修策略。結果表明，該模型能有效地對發電系統可靠性進行量化評估，為制定科學合理的風機維護方案提供了理論支持。

風力發電系統；馬爾可夫過程；可靠性模型；檢修策略；可用度

0 引言

風能作為一種環保清潔的可再生能源，越來越受到世界各國的普遍重視，紛紛采取激勵措施推動本國風電技術行業發展，近十年來全球裝機容量年平均增長率保持在25%左右，現正朝著大容量、高質量的海上風電機組的方向發展。隨著風電機組裝機容量的不斷提高，風電機組的結構也越來越復雜，伴隨機組運行環境的惡劣，致使風力發電系統的故障率居高不下，因此在追求發電容量的同時，必須考慮發電系統運行的可靠性[1]。

目前，國內外對于風電機組的研究主要集中于故障診斷和控制策略等方面[2～4]，在風電機組可靠性評估和運營維護方面研究的還較少，文獻[5]提出了基于馬爾科夫鏈的風機關鍵部件多階段老化模型，用成本效益分析法確立了機組的最優檢修周期；文獻[6]提出了基于半馬爾科夫決策過程的風機多狀態維修優化模型，分析各退化狀態下的維修策略，用策略迭代法法確立了機組的最優維修決策；文獻[7]把風機電氣組件進行拆分，建立了電氣組件系統的可靠性模型，并比較了不同類型風機的可靠性和發電效率；文獻[8]在此基礎上把風機拆分為各個子系統，建立了基于馬爾可夫過程的可靠性模型，構建了機組老化全面修復維修模型。

上述文獻從不同角度研究了風機狀態維護優化模型，對于提高風機可靠性運行有著重要的意義，但是，所建模型中對檢測狀態及檢測時間對系統可用度的影響考慮得還不夠充分。本文在相關研究成果的基礎上，進一步研究雙饋風力發電系統的可靠性計算方法，建立發電系統的可靠性數學模型，深入分析發電系統故障狀態和運行狀態之間相互轉移的過程，結合發電系統的老化過程和實際檢修情況，充分考慮了檢測狀態以及檢測時間對系統可用度的影響，利用改進的狀態空間圖對發電系統建立其狀態檢修模型，以檢修間隔為優化變量，實施風力發電系統檢修策略的優化。

1 發電系統主要結構及故障分析

風力發電系統結構復雜化，為便于研究分析和建模，選取對系統可靠性影響較大的發電機、變流器、電刷滑環等主要部件作為研究對象。由于風電機組通常安裝在偏遠郊外或海岸，運行環境極為惡劣，此外風力發電設備本身設計不當或者質量欠佳等問題，都會影響風機運行的可靠性，根據瑞典風場2000～2004年間故障數據統計表明[9]，發電系統是機組中最常發生故障的系統，也是引起風機停機時間的主要原因，其故障率高達23%。雙饋風力發電系統的工作原理如圖1所示，風輪通過升速齒輪箱與發電機的主軸相連，感應電動機的定子端直接接入電網，轉子端則通過電刷滑環連接變流器后接入電網，只有20%～30%的功率通過變流器經穩壓后傳入電網。

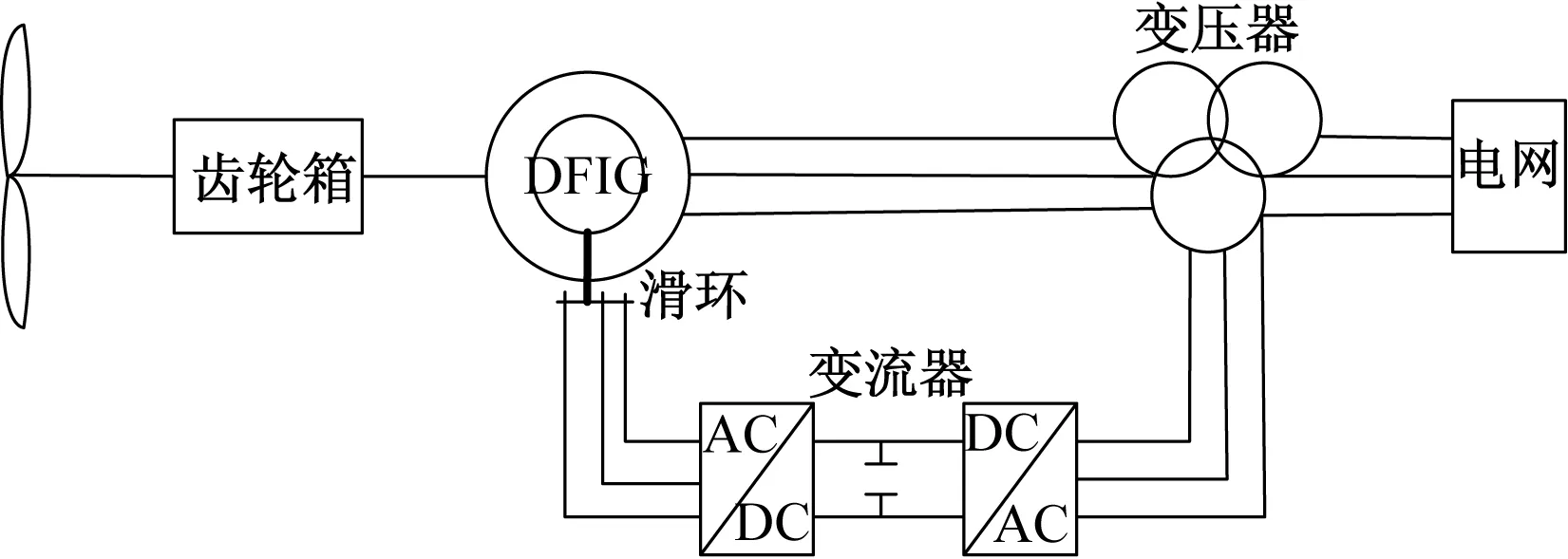
圖1 雙饋感應風力發電機原理圖

雙饋異步發電機是一種繞線式感應發電機，是變速恒頻風力發電機組的核心部件，由于機組運行工況復雜、電網負荷持續變化，易使發電機溫度過高、振動過大而易損壞風力發電機的軸承及繞組的絕緣，因此，故障率明顯高于其他發電機，據統計異步發電機中最常發生故障的部位是軸承、定子、轉子，三者的故障率分別為40%、38%、10%[10]。變流器將風機發出的電能轉換為電壓和頻率都穩定的電能送入電網，采用變速恒頻控制技術，使發電機的轉速隨風力大小而變化，在額定轉速范圍內維持最佳的葉尖速比，同時保證發電機輸出電壓幅值和頻率與電網相同，但高溫發熱、電磁干擾等惡劣因素均影響變流器的工作性能，極易導致變流器故障，且故障主要發生在控制驅動單元、直流母線環節、逆變器等組件中。發電機定子端直接接入電網，而轉子繞組則通過電刷和滑環與變流器相連，據統計在發電系統運行過程中，電刷和滑環之間的機械磨損會影響電機的壽命，其故障率較高，故障還將會引發電機轉子側與變流器連接故障，使部分功率無法通過轉子側饋送到電網。

2 發電系統可靠性建模

2.1 馬爾可夫過程

馬爾可夫過程[11]是一種基于概率統計的特殊隨機過程，能夠描述系統在開始運行后狀態之間相互轉移過程，該過程具備無后效性，即只要系統前一個狀態一經決定，系統的下一個狀態的概率即可確定，并與之前的狀態無關。由于風電機組故障狀態和修復狀態之間的相互轉移是一個隨機過程，而馬爾可夫過程能夠很好描述這種隨機現象，是風電機組運行狀態建模的有力工具。

為了應用馬爾可夫過程建立風力發電系統的可靠性模型，需要做出如下假設：(1)系統部件處于正常或故障狀態，并且兩種狀態可以相互轉換；(2)系統中部件處于正常或故障狀態是互相獨立的；(3)系統部件的故障率和修復率均為常數，即狀態轉移均服從指數分布；(4)只考慮對硬件進行可靠性分析，不考慮軟件和人為因素。

2.2 發電系統的可靠性數學模型

通過對雙饋風力發電系統運行原理與故障機制進行分析，發電系統關鍵部件之間的連接方式并不是簡單的串聯關系，但可以通過運用馬爾可夫過程理論建立發電系統的可靠性模型[7]，令發電機、變流器、電刷滑環分別簡稱為IG、Con、Br，則馬爾可夫狀態轉移關系如圖2所示。

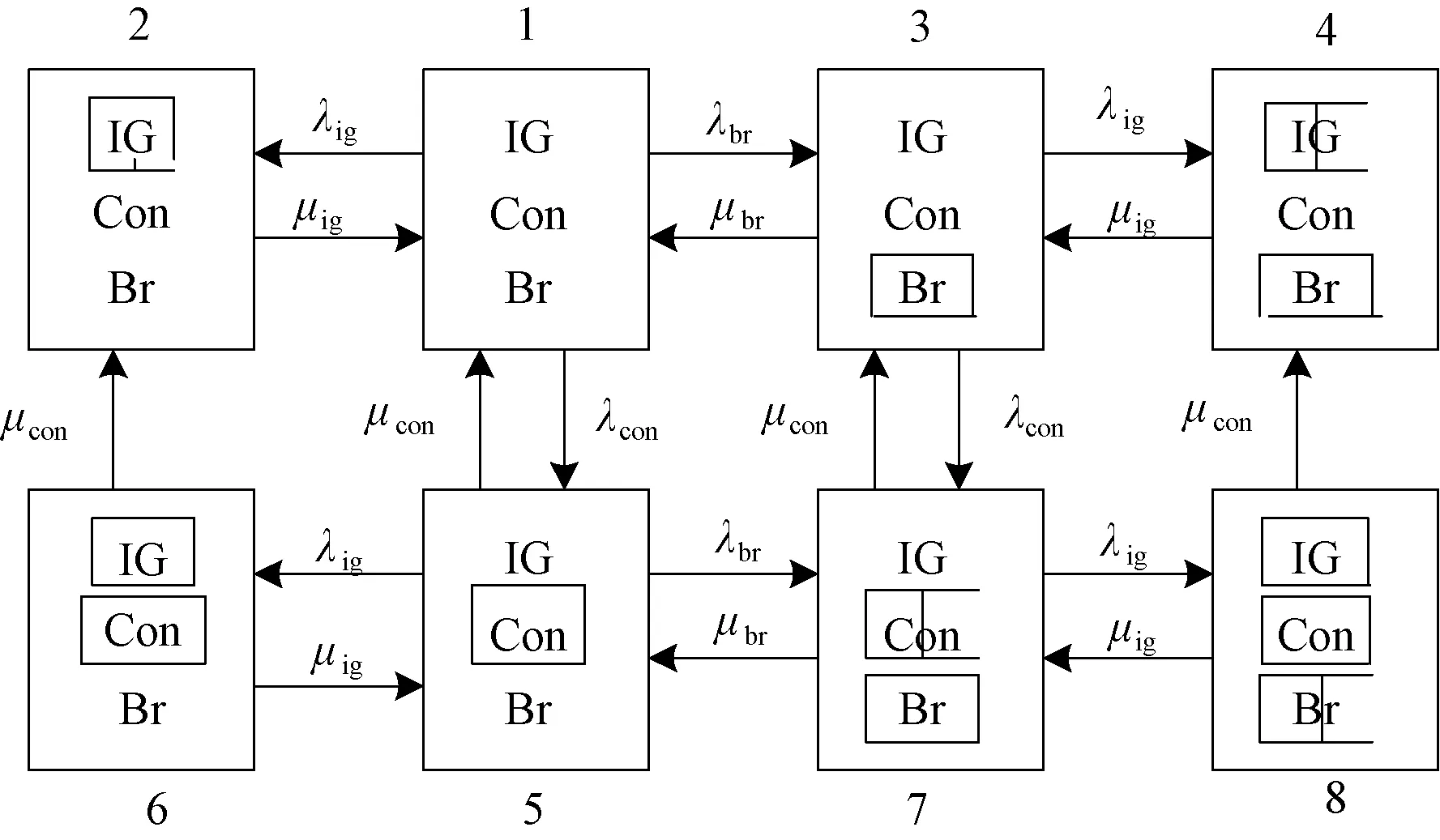
圖2 發電系統的可靠性模型

圖中帶方框的子系統表示該部件處于故障狀態，相反為正常狀態，為了評估發電系統簡化可靠性模型參數，最適合采用頻率平衡法，根據頻率平衡法:

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

式中：λig、λcon、λbr分別為發電機、變流器、電刷滑環的故障率；μig、μcon、μbr分別為發電機、變流器、電刷滑環的修復率。根據風力發電系統處于故障狀態或者運行狀態，可以得到系統簡化的可靠性模型，如圖3 所示。

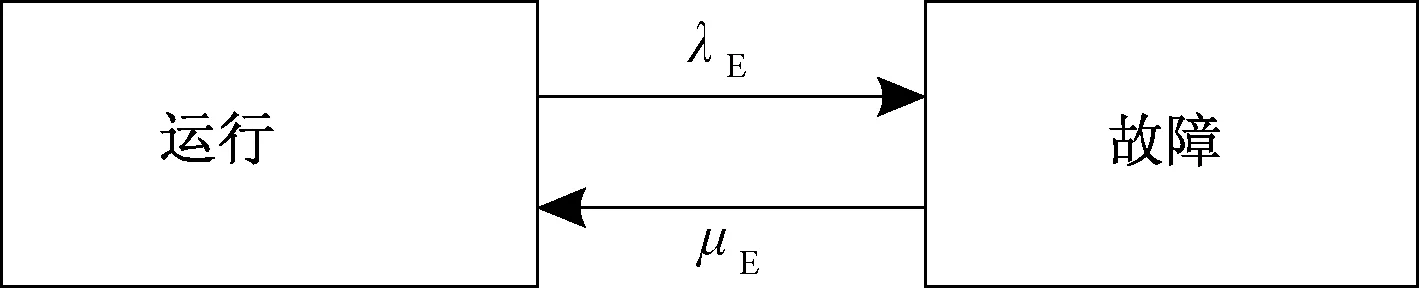
圖3 發電系統簡化后的可靠性模型

根據發電系統運行原理，運行狀態包括圖2中的狀態1、狀態3、狀態5、狀態7，其余狀態為故障狀態，PUp、PDn分別表示系統處于運行狀態和故障狀態的穩態概率，則系統的故障率和修復率如下:

(10)

(11)

(12)

(13)

3 發電系統檢修優化策略

電力設備狀態檢修[12]是一種區別于傳統的事后檢修和定期檢修的新型檢修方式，通常以提高系統可靠度或降低設備風險水平為目標，能有效地解決傳統檢修中的維修不足和維修過剩帶來的問題。發電系統和其他電力設備一樣，在運行過程中可以分為不同的劣化狀態[13]，在對模型進行假設后，系統各狀態之間滿足馬爾可夫過程的無記憶性，各狀態的轉移概率可以用空間狀態圖描述，由于經典狀態圖忽略了檢測狀態及檢測時間，為了更加符合工程實際情況，結合電力設備的狀態維修理論[14，15]，在考慮隨機故障和老化故障的情況下，提出了改進型的狀態空間圖，構造發電系統狀態檢修模型，如圖4所示，得到系統可靠性最優時的維修策略。

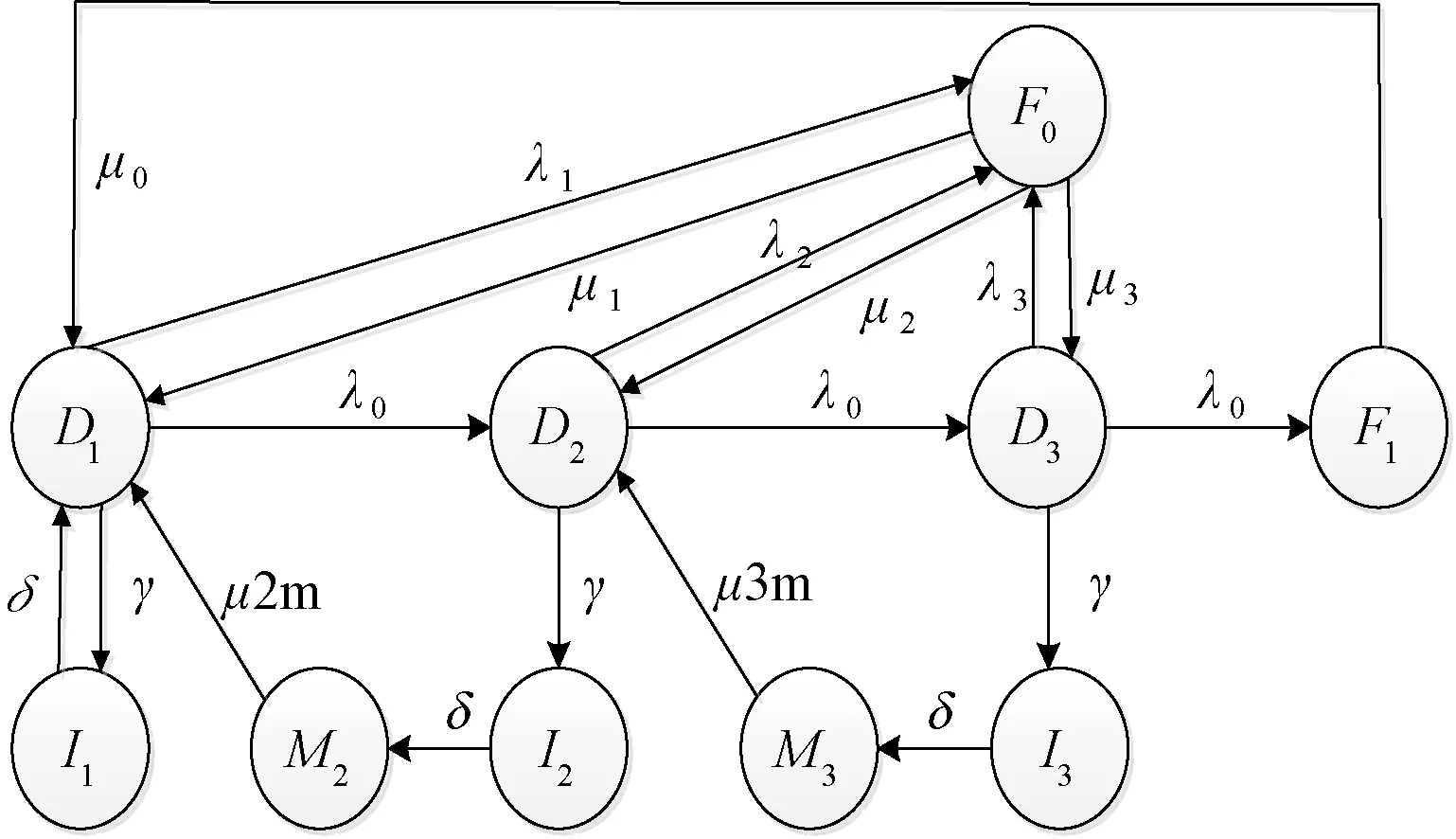
圖4 發電系統老化和隨機故障后的狀態檢修模型

根據發電系統的老化過程與實際檢修情況分析，把發電系統分為3個老化階段分別是D1、D2、D3，λ1、μ1、λ2、μ2、λ3、μ3分別表示系統處在各階段內系統的失效率和修復率；狀態F0、F1分別表示系統處在隨機故障狀態和老化故障狀態，且假設各個老化階段的時間服從均值1/λ0的指數分布，μ0是系統老化故障后的維修率；I1、I2、I3分別表示系統處在各老化狀態時所對應的檢測狀態，1/γ為系統各狀態的平均檢測間隔時間，1/δ為各系統平均檢測時間；M2、M3表示系統經過檢測后進行的預防性維修狀態，1/μ2m、1/μ3m分別表示系統處在D2、D3老化階段內平均預防性維修時間。

在上述維修模型中，如果對系統不采取任何維修措施，系統將經過3個老化階段最終進入老化故障狀態F1，經過維修后系統可恢復到狀態D1，除了D1狀態不需要進行預防性維修外，其余老化狀態下都需要采取預防性維修，系統可恢復至前一個狀態，每次采取預防性維修前，要先對系統進行檢測，確定系統狀態和采取的檢修動作；系統除了發生老化故障外，還會因偶發故障而進入隨機故障狀態F0，此時對設備進行故障后維修，系統可恢復至故障前的狀態。

根據發電系統狀態檢修模型，運用馬爾可夫過程原理，可得出發電系統檢修模型的狀態轉移矩陣如下所示：

(14)

根據馬爾可夫狀態轉移矩陣，得出發電系統狀態的穩態方程組：

(15)

式中:P=[PD1PD2PD3PF1PF0PI1PI2PM2PI3PM3]，P中的各元素分別表示為狀態D1、D2、D3、F1、F0、I1、I2、M2、I3、M3的穩態概率。根據風力發電系統老化檢修模型和狀態轉移概率矩陣，發電系統的正常運行的概率為：

(16)

4 實例計算及參數分析

目前，風電機組歷史故障數據資料還比較少，這使得發電系統的可靠性參數很難獲取，本文中發電機、變流器可靠性數據參考文獻[8]，而電刷滑環可靠性數據很少有文獻提及，可參考某風場歷史數據，風力發電系統各個部件的故障率和修復率，如表1所示。

表1 風機發電系統各部件3個老化階段的可靠性數據

根據風場實際運營情況，發電系統的整體設計壽命為20年，采集風場發電系統的維護時間和維護次數，系統平均每次檢測所需的時間為0.1天，第二劣化階段的平均預防性維修需2天，第三劣化階段的平均預防性維修需2.5天，系統老化故障后事后維修平均需要28天。

根據上表各部件的可靠性數據，計算得出發電系統可靠性數據，采用MATLAB編程軟件進行數值計算分析，可得到該系統的檢測平均間隔時間(1/γ)以及平均檢測率(δ)對可用度的影響結果，分別如圖所示。

由圖5可以看出，系統的穩態可用度隨檢測平均間隔時間的增大而提高，當檢測平均間隔時間為0.50年左右時，系統可用度緩慢上升逐漸趨于平穩狀態，當檢測平均間隔時間達到0.75年時，系統的可用度達到最大且為0.996 8。由圖6看出，開始時系統的可用度隨著檢測時間的減少而增大，但當檢測率達到20 000次時，即每次檢測0.44 h左右時，系統的可用度趨于常數，檢測可以發現設備的潛在故障，進行預防性維修，但檢測本身不能使設備老化狀態發生改變。

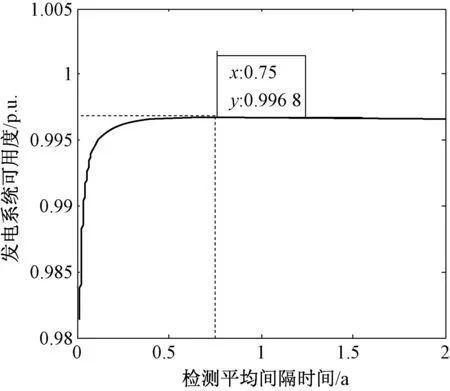
圖5 檢測平均間隔時間對系統可用度的影響

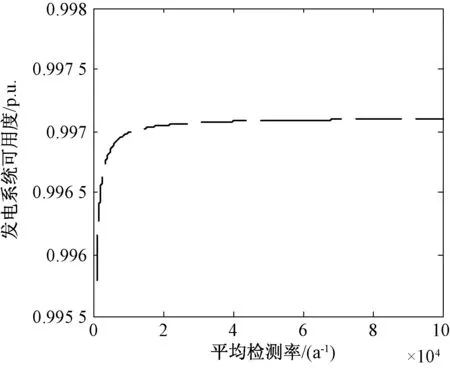
圖6 平均檢測率對系統可用度的影響

發電系統在實際運行中，由于運行環境的差異或不同類型風電機組材質的不同，機組的老化程度也會不同[16]，因此，本文探究不同老化程度的發電系統檢測平均間隔時間與系統穩態可用度的關系，如圖7所示。

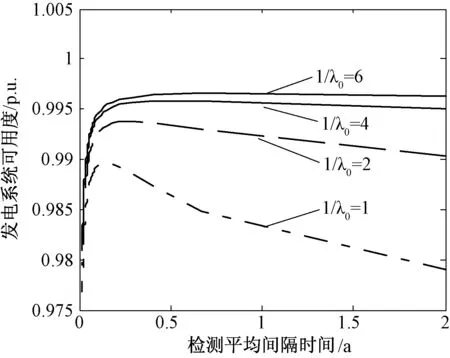
圖7 不同老化系統檢測平均間隔時間對可用度的影響

圖7表明，發電系統的可用度與機組的老化程度有著重要的關系，老化間隔時間(1/λ0)越長，系統的穩定運行性能越好，系統的可用度也隨著老化間隔時間的增大而提高。當系統老化間隔確定時，系統的可用度會隨著機組的檢測平均間隔時間先提高而后緩慢下降，因此檢測平均間隔時間將會很大程度上影響系統的穩態可用度，不同老化系統存在最優的檢測平均時間間隔，系統所對應的可靠度最優的檢修策略如表2所示。

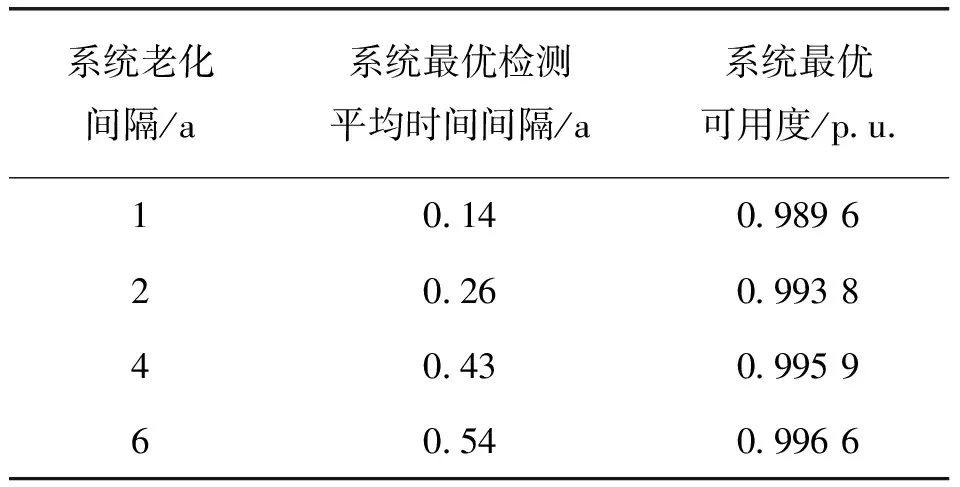
表2 可靠度最優時的檢測策略

5 結論

本文在分析發電系統的運行原理和故障機制的基礎上，建立了發電系統的可靠性數學模型，在考慮隨機故障和老化故障的情況下，提出基于馬爾可夫過程的改進型多狀態維修模型，能有效地描述系統的性能退化過程并參考現有風場的可靠性數據，通過對檢測平均間隔時間的優化，得出了不同老化間隔系統最優時的檢修策略，為風電機組的檢修工作人員進行優化檢修提供了有力地理論支持。

風力發電機組是集機械、電氣多部件的復雜系統，故障模式及運行狀態復雜多樣，運用馬爾可夫過程簡化了修復模型的分析，但是忽略了不同狀態之間的持續時間，考慮系統多種狀態模式，深入分析部件故障間的關系，建立涵蓋多個風電機組的綜合狀態模型，實行聯合檢修的優化策略，還有待進一步研究。

[1]Tavner P J，Xiang J，Spinato F．Reliability analysis for wind turbines [J]．Wind Energy，2007，10(1)：1-18.

[2]彭華東，陳曉清，任明，等．風電機組故障智能診斷技術及系統研究[J]．電網與清潔能源，2011，27(2)：61-66.

[3]高揚，于會群，張浩，等．變速恒頻雙饋風力發電系統并網控制仿真[J]．電力科學與工程，2014，30(2)：1-6.

[4]李國棟，魏春，韓民曉．采用網側TCVR的雙饋風機低電壓穿越控制策略研究[J]．華北電力大學學報，2012，39(4)：24-29.

[5]溫子明．關于風力發電機組優化檢修的探討[J]．電子世界，2012，(4)：36-37.

[6]蘇春，周小荃．基于半馬爾科夫決策過程的風力機狀態維修優化[J]．機械工程學報，2012，48(2)：44-49.

[7]Arabian H H， Oraee H，Tavner P J．Wind turbine productivity considering electrical subassembly reliability[J]．Renewable Energy，2010，35(1)：190-197.

[8]李大字，馮園園，劉展，等．風力發電機組可靠性建模與維修策略優化[J]．電網技術，2011，35(9)：122-127.

[9]Ribrant J， Bertling L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005[J]． IEEE Transactions on Energy Conversion，2007，22(1)：167-173.

[10]Popa L M， Jensen B B，Ritchie E，et al．Condition Monitoring of Wind Generators [J]．IEEE Industry Applications Society Annual Meeting，Salt Lake City, UT, USA, 12-16 October 2003:1839-1846.

[11]曹晉華，程侃．可靠性數學引論[M]．北京：高等教育出版社，2012.

[12]李景祿，李青山．電力系統狀態檢修技術[M]．北京：中國水利水電出版社，2011.

[13]Welte T M．Using state diagrams for modeling maintenance of deteriorating systems[J]．IEEE Transactions on Power Systems，2009，24(1)：58-66.

[14]汲國強，吳文傳，張伯明，等．一種適用于狀態檢修的電力設備時變停運模型[J]．中國電機工程學報，2013，33(25)：139-146.

[15]姜學蕾．基于馬爾可夫過程的電力設備檢修優化決策[D]．濟南：山東大學，2013.

[16]Byon E，YU D．Season-dependent condition-based maintenance for a wind turbine using a partially observed Markov decision process[J]． IEEE Transactions on Power Systems，2010，25(4)：1823-1834．

Reliability Modelling and Maintenance Strategy Optimization for Wind Power System

Qin Yang， Ma Huimin， Zhu Tianwei， Zhu Qinghua

(School of Electric Engineering, Shanghai Dianji University, Shanghai 200240, China)

Aiming at the problems related to reliability evaluation and operational maintenance for the wind power system, the operation principle and fault mechanism of the doubly-fed induction wind turbines were studied, and the reliability model of the double fed induction generation system was established using Markov process and reliability theory. Considering random failure and aging failure of the system an improved maintenance model for power generation system was proposed. The state transition matrix was obtained by using the relationship of the state transition, and the availability of system was solved by MATLAB software. The influence of detection time on system availability was also discussed. Finally maintenance srategies for different aging power generation systems with optimal reliability were obtained. The results indicate that the model can effectively evaluate the reliability of wind power system and provides theoretical support for the formulation of scientific maintenance schemes for wind turbines.

wind power system；markov process；reliability model；maintenance strategy；availability

2015-05-11。

上海市大學生創新活動計劃項目(G2-13DXSCX-003)。

秦洋(1989-)，男，碩士研究生，主要研究方向為風電機組的可靠性建模與維修策略的優化，E-mail：qinxueyang1989@163.com。

TM614

A

10.3969/j.issn.1672-0792.2015.07.010