基于分支程序逆向評估的安全多方計算

俞強生，古天龍，徐周波，寧黎華

(桂林電子科技大學 廣西可信軟件重點實驗室，廣西 桂林541004)

計算機和網絡技術的迅猛發展為多方聯合計算提供了大量應用場景。然而，信息化發展帶來便利的同時，數據安全與隱私保護問題不斷凸顯，成為制約多方聯合計算發展的最大障礙。安全多方計算(secure multi-part computation，簡稱SMC)概念最早由圖靈獎獲得者Yao提出［1］，其核心思想是在保護隱私的前提下，互不信任的參與方進行聯合計算，并得到預期執行結果。安全多方計算在隱私保護基因計算［2］、保密計算［3］等許多領域有廣泛應用。

決策函數有效表示問題是安全多方計算研究的熱點問題，決策函數表示是否高效決定了協議效率的高低。Yao［4］最早提出用混淆布爾電路的方法解決決策函數表示問題，但布爾電路不能描述偽布爾函數。同時，隨著決策函數復雜性增加，布爾電路中的電路門規模急劇增大，造成編碼規模大、計算復雜度高等問題。

符號描述技術是一種求解決策函數表示問題的新方法，其中有序二叉決策圖(ordered binary decision diagram，簡稱OBDD)是布爾電路的一種緊湊表示方式。Kruger于2006年提出基于OBDD技術描述決策函數［5］，一定程度上降低了編碼復雜度，提高了協議效率。但是，OBDD是布爾電路方法基礎上的一種形式化表示，也不能描述偽布爾函數。在文獻［5］基礎上，古天龍等［6］提出基于代數決策圖(algebraic decision diagram，簡稱ADD)技術取代符號OBDD刻畫決策函數，決策函數的表示形式由此得到極大擴展。然而，符號ADD隨著決策函數復雜性增加，葉子節點規模會急劇膨脹，協議面臨狀態空間爆炸問題。

安全計算借助可編程通用電路，將函數描述及隱私數據作為輸入，進行聯合計算并輸出結果［7］，但是，由于布爾電路本身固有的局限性，描述效率不夠理想。因此，Brickell等［8］使用分支程序(branching program，簡稱BP)表示安全計算問題。為減少交互次數，降低協議復雜度，Mohassel［9］結合不經意傳輸技術，提出基于不經意傳輸BP的安全計算協議。

邊值二叉決策圖(edge-valued binary decision diagram，簡稱EVBDD)作為表示偽布爾函數的一種新型數據結構，極大改善了偽布爾函數和有限域取值函數的描述能力，在一定程度上解決了因決策函數規模增大而導致的狀態空間爆炸問題。為此，引入EVBDD的符號描述技術，利用其易操作和高緊湊性的優點，給出一種基于EVBDD的決策函數表示方法，并設計一個效率高、評估計算簡單且適用大多數決策函數的基于符號EVBDD的安全2方計算協議。同時，在分支程序的基礎上，提出一種分支程序的逆向評估方法，借助基于邊值二叉決策圖的安全2方計算協議為基礎協議，設計一個基于分支程序逆向評估的安全多方計算協議，此協議將傳統的2方計算擴展到多方，其效率也有所提高。

1 預備知識

1.1 不經意傳輸協議

定義1［10］2選1不經意傳輸協議(O):參與者按行為劃分為發送方和選擇方。發送方輸入一串長為t的字符串對∈{0，1}t，其中i=1，2，…，n，選擇方輸入選擇位b∈{0，1}。協議執行完畢，選擇方獲得字符串，但無法知曉另一字符串，而發送方也無法獲知選擇方的選擇b。

1.2 同態加密(HE)

使用一種語義安全的加同態公鑰加密機制，加密機制的語義安全是指無法從特定密文中提取任何明文信息。

加同態加密算法具有如下性質:存在有效算法⊕，E(x+y)=E(x)⊕E(y)或x+y=D(E(x)⊕E(y))成立，并且不泄漏x和y。因此，加同態算法也可直接用于與常數k的乘法操作:kE(x)=E(kx)。對同態加密的實例化采用文獻［11］中的加密機制。

2 基于符號EVBDD的安全2方計算協議(協議1)

2.1 邊值二叉決策圖(EVBDD)

EVBDD［12］是在ADD的基礎上，在邊中引入權值提高子圖的共享度，進而為函數值是整數的偽布爾函數提供一種更為規范、緊湊的表示形式。EVBDD不僅能像OBDD一樣實現布爾函數操作，還能像ADD一樣實現對偽布爾函數的布爾操作和算術操作。這里，決策函數的EVBDD表示建立在有序的基礎上。圖1和圖2是偽布爾函數f=3+5x1+6x2+x3分別在ADD和EVBDD符號表示下的圖形結構，變量序為x1＜x2＜x3。在輸入模式(0，1，0)下，函數f對應的函數值為3+0+6+0=9。

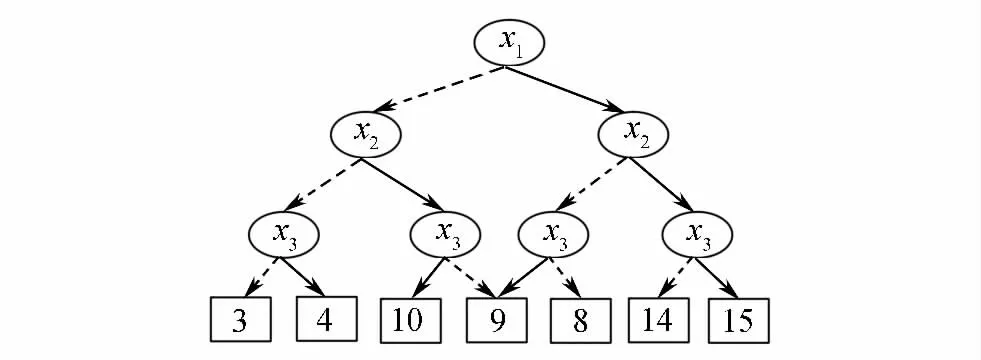
圖1 偽布爾函數f=3+5x1+6x2+x3 ADD表示Fig.1 ADD for pseudo-Boolean functionf=3+5x1+6x2+x3

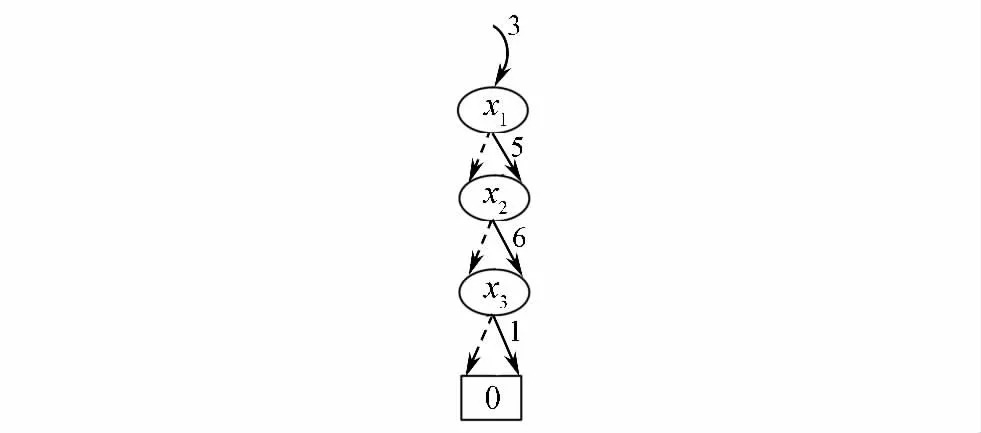
圖2 偽布爾函數f=3+5x1+6x2+x3 EVBDD表示Fig.2 EVBDD for pseudo-Boolean functionf=3+5x1+6x2+x3

2.2 協議流程

在符號EVBDD表示的基礎上，提出基于符號EVBDD的安全2方計算協議。假設參與計算雙方為Alice和Bob，輸入為:表示(偽)布爾函數f(x1，x2，…，xn)的EVBDD(f)，其中變量序為x1＜x2＜…＜xn。Alice的輸入Xa=(x1，x2，…，xk)對應EVBDD(f)中前k個變量，Bob的輸入Xb對應后n-k個變量。預期輸出為:C=f(Xa，Xb)。

參與方Alice執行協議的流程為:

1)用變量(x1，x2，…，xk)遍歷EVBDD(f)的前k個節點，約束后的初始節點記為v。

2)約束后的EVBDD(ffull|Xa)隨機產生n-k對節點的取值密鑰:，并為每個節點v分配節點密鑰sv。

3)為k+1層到n層的每個節點隨機分配一個標簽，用l(v)表示節點v所處的層數。

4)為約束后的EVBDD(ffull|Xa)填充虛節點。

5)加密EVBDD(ffull|Xa)，每個節點密文都包含代表該節點位置的節點標簽、該節點不同取值下的2條子密文。每條子密文又包含路徑中下一節點的標簽、下一節點的節點密鑰、該節點取值時的邊值(也稱權值)。

6)Alice將k+1層到n層的節點密文和初始節點的節點密鑰sv發送給Bob。

參與方Bob執行協議的流程為:

1)Bob獲取初始節點的節點密鑰sv，并通過nk次1-out-of-2不經意傳輸獲得對應其輸入的密鑰

2)Bob用獲得的密鑰解密，從Alice步驟5)獲取的密文得到C，即f(Xa，Xb)。

3 基于分支程序逆向評估的安全多方計算

3.1 分支程序

定義2［9］分支程序:分支程序是3元組〈{P1，P2，…，Pz}，L，R〉的有向無環圖，其中Pi(i=1，2，…，z)為節點集，且滿足以下條件。

1)P1，P2，…，Pd為決策節點(又稱內部節點、非終節點)，Pd+1，Pd+2，…，Pz為分類節點(終節點)。

2)每個決策節點Pi(1≤i≤d)對應一個2元組〈ti，αi〉，對應輸入值V=v1，v2，…，vn。其中，ti為閥值，αi為輸入索引，vai為索引αi下的輸入值。

3)分類節點(又稱診斷節點、終節點)即為葉子節點，每一個葉子節點都持有唯一的標簽〈di〉。

4)L和R分別表示決策點Pi的左右分支索引函數的有向無環圖，若vai≤ti，索引為L(i)，反之，則為R(i)。

分支程序的評估始于節點P1，若va1≤t1，h=L(1)，否則，h=R(1)。重復此過程計算Ph，直到獲取葉子節點。從分支程序的評估過程可知，評估順序從初始節點依次到葉子節點，稱為順序評估，順序評估的優點在于評估層次明顯，過程簡單。

3.2 分支程序的逆向評估

由分支程序的評估過程可知，評估信息需要交互。若考慮隱私因素，參與對象只能局限于2方，即所有決策節點為1方所有。鑒于此，引入分支程序的逆向評估方法，評估順序從葉子節點依次逆向直到初始節點，如此節點之間無需信息交互，各個評估節點可分屬不同參與方所有。其逆向評估過程如下:假設分支程序為〈{P1，P2，…，P15}，L，R〉，其中P1，P2，…，P10為決策節點，P11，P12，…，P15為葉子節點，評估輸入V=v1，v2，v3，v4。如圖3、4所示，參與者4開始評估第4層節點，得到相應葉子節點信息1、2、3、4，用此信息替代第4層節點內容。依次逆向評估第3層節點，參與者3將評估得到的第4層節點的葉子節點信息替代第3層節點內容，如此直到唯一一個葉子節點信息替代初始節點內容，評估結束。

圖3 分支程序葉子節點評估Fig.3 The leaf nodes evaluation of branch program

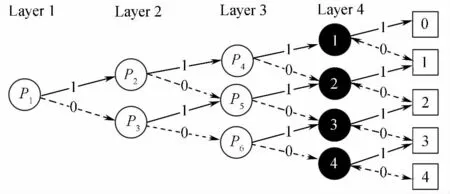
圖4 分支程序第4層節點評估Fig.4 The fourth layer nodes evaluation of branch program

3.3 基于分支程序逆向評估的安全多方計算協議(協議2)

良好的隱私保護和對決策函數的有效表示是降低安全多方計算協議復雜度、提高協議效率的關鍵所在。為此，將安全多方計算任務分割成若干個子任務，在分支程序中不同決策節點處理不同子任務。其中，借助基于EVBDD的安全2方計算協議為基礎協議，分別處理各個子任務。

基于分支程序逆向評估的安全多方計算協議需要分3步:分支程序的混淆處理、不經意傳輸選擇和安全計算的逆向評估。為保證隱私得到保護，需要將分支程序T轉換成混淆的分支程序T′。假設輸入V=v1，v2，…，vn，其長度為l，具體算法如下。

算法1分支程序的混淆處理。輸入:分支程序T=〈{P1，P2，…，Pk}，L，R〉，pi=〈ti，αi〉為決策節點，其中i=1，2，…，d，pi=〈di〉為葉子節點，i=d+1，d+2，…，k。輸出:1)混淆后的安全分支程序T′。2)k對隨機l+l′值b1，b2，…，bk。3)2kl對隨機邊值密鑰，其中1≤i≤k，1≤j≤l。

算法步驟為:

1)令Q為集合{1，2，…，k}的隨機置換函數，且Q［1］=1。

2)為所有k個決策節點分配節點密鑰λ1，λ2，…，λk。

3)對i=1，2，…，k進行遍歷。

4)為節點i分配邊值密鑰，，其中，j=1，2，…，l。

6)對所有節點編號進行混淆，令ι=Q［i］。

7)若Pi是葉子節點，即Pi=〈di〉，則令Si={“label”，di}λι。

8)若Pi是決策節點，即Pi=〈ti，αi〉，則借助基于符號EVBDD的安全2方計算協議來刻畫評估該節點，并根據該EVBDD的最終計算結果x，計算x-(b′imod 2l)。

9)若步驟8)的計算結果小于閥值ti，則轉向左分支L，否則轉向右分支R。其中，L=(Q［L(i)］，KQ［L(i)］)，R=(Q［R(i)，KQ［R(i)］)，所有被評估計算的決策節點標記為C。

10)對決策節點內容進行加密:Si={Ci}λι。

11)協議輸出:T′=〈{S1，S2，…，Sk}，k1〉，協議結束。

算法2不經意傳輸選擇。輸入:長為l的值V=v1，v2，…，vn，混淆后分支程序T′中的閥值ti，索引αi和混淆值bi。輸出:1)s1，s2，…，sk，其中對于任意i有si=vai+(bimod 2l)。2)對于任意i，用邊密鑰wi1，wi2，…，wil加密si，其中si又等價于vai+(b′imod 2l)。

算法步驟為:

1)各參與方構造相應的同態加密方案，并將公鑰發送給服務器。

全省礦業綠色發展現場會在湖州召開（省廳新聞宣傳中心） ............................................................................9-6

2)對i=1，2，…，k進行遍歷。

3)參與方對各自的隱私輸入進行加密，并將加密結果E［vi］發送給服務器。

4)服務器接收公鑰以及密文E［vi］，同態計算E［vai+bi］=E［vai］+E［bi］，將結果返回參與方。

5)參與方用私鑰對E［vai+bi］進行解密，得到vai+bi。令si=vai+(bimod 2l)=vai+(b′imod 2l)。

6)對j從1到l進行遍歷。

在算法2獲取邊密鑰的基礎上，參與者利用服務器提供的節點密鑰對混淆后的安全分支程序進行逆向計算評估，具體算法如下。

算法3安全計算逆向評估。輸入:混淆后的安全分支程序T′、索引向量h、節點密鑰λh以及邊密鑰wi1，wi2，…，wil。輸出:葉子節點信息m=T(V)。

算法步驟為:

1)參與方根據節點密鑰kh對混淆后的分支程序T′的倒數第2層決策節點(已加密)進行解密，得到決策節點Ch。

2)若決策節點Ch不是初始節點，則利用基于符號EVBDD的安全2方計算協議以及輸入wh1，wh2，…，whl對該決策節點進行評估計算，否則轉向步驟6)。

3)將上述計算結果(即葉子節點信息)標記為M。

4)將M替代已經解密的決策節點Ch，并令h=h-1。

5)轉向步驟2)。

6)評估計算初始節點，獲取最終結果m=T(V)，協議結束。

本協議引入分支程序逆向評估技術，并在內部決策節點分配不同子任務，使協議的評估參與者由2方擴展到多方。同時，借助基于EVBDD的安全2方計算協議處理各個不同子任務，提高了決策函數的描述效率，保障了協議的隱私安全。

4 協議的正確性、安全性和效率分析

4.1 正確性分析

1)協議1的正確性。假設Alice成功構造決策函數的EVBDD結構，在約束Xa=(x1，x2，…，xk)下，添加相應虛節點得:f|Xa。Bob無法得知約束前Alice輸入的Xa及約束后的EVBDD結構。Alice為約束后EVBDD結構中的各個節點分配1個節點密鑰sv，并連同解密后的節點密文一起發送給Bob。同時，Alice根據Bob的可能取值為所有非葉子節點分配1對取值密鑰)，假設此時π=0。設Bob得到加密后的節點為pv，其密文中的2條子密文為c1、c2，Bob根據此節點取值π，經過不經意傳輸協議在Alice對應該節點的取值密鑰對中，獲得其中1個取值密鑰。Bob根據sv和即可解出2條子密文中的1條，得到計算路徑中節點pv的下一個節點的位置以及加密后新的2條子密文。重復上述步驟即可到達葉子節點，得到正確計算結果。由此，可知協議的正確性。

2)協議2的正確性。參與方通過算法2不經意傳輸選擇協議得到邊密鑰wi1，wi2，…，wil，通過算法3獲取節點密鑰λh、安全分支程序T′和索引向量h。令葉子節點信息為M={m1，m2，…，mn}，參與方1根據輸入逆向評估計算出信息M1={m1，m2，…，mk}(1≤k≤n)，用此信息替換參與方1所在決策節點信息。然后，參與方2根據其輸入逆向計算出信息M2={m1，m2，…，mt}(1≤t≤k)，用此信息替換參與方2所在決策節點信息。由于分支程序決策節點內部的計算以協議1為基礎協議，決策節點內部結構圖的計算正確。以此類推，依次逆向評估計算，最終正確計算出唯一的一個葉子信息m。因此，協議2是正確的。

4.2 安全性分析

1)協議1的安全性。假設Alice提供節點密鑰為sv(v=1，2，…，n-k)，節點的取值密鑰為，。Bob首先獲取相應節點密鑰，然后通過1-out-of-2不經意傳輸協議獲取唯一的取值密鑰，即和兩者中只能獲取其中一個，同時Alice無法得知Bob的選擇信息，這就確保了計算雙方的隱私都能得到保護。Bob用獲取的節點密鑰和該節點的取值密鑰可解密出該節點在相應取值后的下一節點，而且是唯一的。以此類推，能得到唯一的一條路徑安全地到達葉子節點。由此可見，在這條唯一計算路徑的求解過程中，參與者的信息都得到了保護。

2)協議2的安全性。服務器通過算法1混淆后的分支程序是安全的。算法2通過同態加密E［vai］對輸入數據進行加密，并通過混淆值si=vai+(bimod 2l)=vai+(b′imod 2l)對輸入數據進行混淆，保證了參與各方輸入隱私的安全性。參與方在算法2中通過不經意傳輸選擇協議得到不同分支中的唯一一個分支邊密鑰，這里的唯一性是由OT12所決定的。結合節點密鑰計算出唯一的葉子節點信息。由于邊密鑰的唯一性，確保評估計算過程中信息安全。由于決策節點的內部評估以協議1為基礎協議，其安全性分析同協議1。此外，逆向評估計算避免了參與各方之間的信息交互，提高了協議的安全性。因此，協議2是安全的。

4.3 效率分析

5 結束語

針對傳統決策函數表示計算復雜度高、編碼規模大以及參與者局限于2方問題，提出一種基于邊值二叉決策圖和分支程序逆向評估的解決方案。與文獻［9］相比，不僅將協議擴展到多方，而且降低了決策函數的復雜度，提高了協議效率。

由于分支程序逆向評估計算僅考慮了2分支的情況，在下一步工作中，可對多分支程序逆向評估計算進行研究。此外，基于EVBDD的決策函數描述方式，由于邊權重因子的出現，協議中節點的存儲變得更加復雜。因此，基于EVBDD決策函數描述的優化將是今后研究的方向。

［1］Yao A.Protocols for secure computations［C］//Proceedings of the 23th Annual Aymposium on Foundations of Computer Science，IEEE，1982:160-164.

［2］Katz J，Malka L.Secure text processing with applications to private DNA matching［C］//Proceedings of the 17th ACM Conference on Computer and Communications Security，2010:485-492.

［3］李順東，王道順.基于同態加密的高效多方保密計算［J］.電子學報，2013，41(4):798-803.

［4］Yao A.How to generate and exchange secrets［C］//Proceedings of the 27th Annual Symposium on Foundations of Computer Science，IEEE，1986:162-167.

［5］Kruger L，Jha S，Goh E，et al.Secure function evaluation with ordered binary decision diagrams［C］//Proceedings of the 13th ACM Conference on Computer and Communications Security，2006:410-420.

［6］古天龍，何仲春，常亮等.基于符號ADD和線性多分支程序的分類算法安全評估［J］.電子學報，2014，42(5):940-947.

［7］Kolesnikov V，Schneider T.A Practical Universal Circuit Construction and Secure Evaluation of Private Functions［M］//Financial Cryptography and Data Security.［S.l.］:Springer Berlin Heidelberg，2008:83-97.

［8］Brickell J，Porter D，Shmatikov V，et al.Privacy-preserving remote diagnostics［C］//Proceedings of the 14th ACM Conference on Computer and Communications Security，2007:498-507.

［9］Mohassel P，Niksefat S.Oblivious Decision Programs from Oblivious Transfer:Efficient Reductions［M］//Angelos D.Financial Cryptography and Data Security.［S.l.］:Springer Berlin Heidelberg，2012:269-284.

［10］Rabin M.How toExchange Secrets by Oblivious Transfer［R］.Harvard University，1981.

［11］Paillier P.Public-key cryptosystems based on composite degree residuosity classes［C］//Advances in Cryptology-EUROCRYPT’99.［S.l.］:Springer Berlin Heidelberg，1999:223-238.

［12］古天龍，徐周波.有序二叉樹決策圖及應用［M］.北京:科學出版社，2009:17-57.