一類弱非線性互補問題的模系矩陣多分裂迭代算法

夏澤晨，李郴良

(桂林電子科技大學 數學與計算科學學院，廣西 桂林541004)

互補問題在力學、工程、經濟、交通等研究領域有著廣泛的應用，如力學中的接觸問題、彈塑性問題，工程中的障礙和自由邊界問題、流體彈性動態(tài)潤滑問題、最優(yōu)控制問題、交通平衡問題以及經濟均衡問題等，均可歸結為互補問題。關于互補問題的研究一直是計算科學的熱點問題，受到眾多專家學者的關注。

關于用迭代法求解線性互補問題，Bai Zhongzhi［1］提出了一類模系分裂迭代算法，該算法通過將線性互補問題變換為一類與它等價的不動點方程組進行迭代計算。在此基礎上，Bai Zhongzhi等［2］提出了模系矩陣多分裂迭代算法，該算法顯示出較好的計算效果。張麗麗［3］總結了關于互補問題的模系矩陣分裂迭代算法，介紹該系列算法的一個通用框架以及一系列的模系松弛迭代方法。Li Chenliang等［4］提出了多重Schwarz算法，將多重分裂算法的求解范圍擴大到了對角凸非線性互補問題，并推廣了該類方法的適用范圍。

本研究主要考慮一類弱非線性互補問題［5］的快速算法。Noor［5］通過變量變換把這類互補問題轉化為一類與之等價的不動點方程組，并討論有關這類弱非線性互補問題的算法。本研究將模系矩陣多分裂迭代算法推廣到求解這類弱非線性互補問題，提出一種新的求解方法。

1 預備知識

弱非線性互補問題:

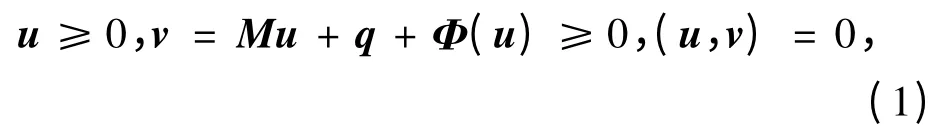
其中矩陣M∈Rn×n，向量q∈Rn，非線性項Φ(u)滿 足Φ(u)=(α1(u1)，α2(u2)，…，αn(un))T，αi(ui)為一個定義域在實數上的實函數。

定義矩陣A=(aij)m×n，B=(bij)m×n∈Rm×n。設A≥B(A＞B)，有且僅有aij≥bij(aij＞bij)滿足所有的1≤i≤m，1≤j≤n。若0為一個零矩陣且滿足A≥0(A＞0)，則A為非負矩陣。定義為非負矩陣，且其元素為

令A∈Rn×n為一個實n階矩陣，其比較矩陣

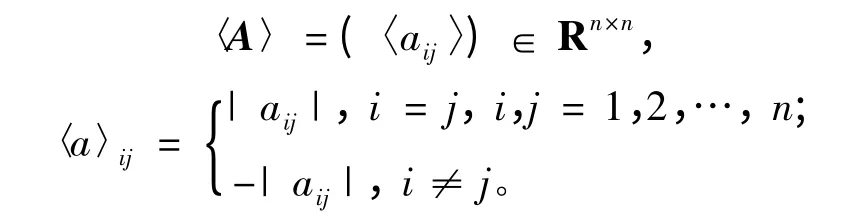
若其非對角元素是非正的并且其逆矩陣A－1≥0，矩陣A稱為一個M-矩陣;若M-矩陣A的比較矩陣〈A〉也是一個M-矩陣，則矩陣A被稱作一個H-矩陣;若其對角矩陣是正的，則H-矩陣A被稱為H+-矩陣，若A為一個M-矩陣，Ω為一個正對角矩陣，當滿足A≤B≤Ω時，則矩陣B為一個M-矩陣。

假設A=F－G，若F為一個非奇異的矩陣，則A=F－G被稱為矩陣A的一個分裂;對于分裂A=F－G，若〈A〉=〈F〉－|G|，則這個分裂被稱為H-相容分裂。若A=F－G為一個H-相容分裂，則有:

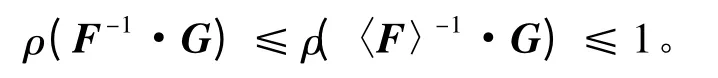
引理1［6］令A∈Rn×n為一個H-矩陣，D=diag(A)，B=D－A，則

1)矩陣A為非奇異;

2)|A－1|≤〈A〉－1;

引理2［7-8］(Perron-Frobenius定理)令A∈Rn×n為一個不可約非負矩陣，

1)ρ(A)為矩陣A的譜半徑;

2)譜半徑ρ(A)的特征向量x是一個正向量;

3)ρ(A)為矩陣A的一個特征值;

4)若矩陣A的任意一個元素增加，則ρ(A)增加。

利用相關概念，易證定理1。

定理1設M=F－G為矩陣M∈Rn×n的一個分裂，Ω為一個正對角陣，對于弱非線性互補問題(1)，以下結論成立:

1)若(u，v)為弱非線性互補問題(1)的一個解，則滿足以下不動點方程組:

2)若x滿足不動點方程組(2)，則有

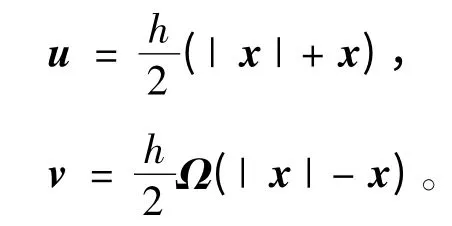
這對向量(u，v)是弱非線性互補問題(1)的一個解。

2 模系多分裂迭代算法

在給出新的算法之前，引入如下矩陣多分裂概念。

定義1［7］設M∈Rn×n，l∈Z+且l≤n，若對于k=1，2，…，l，M=Fk－Gk為矩陣M的分裂，Ek∈Rn×n為非負對角矩陣，且滿足則稱(Mk，Nk，Ek)(k=1，2，…，l)為矩陣M的一個多分裂。

由定理1得到一個與弱非線性互補問題(1)等價的不動點方程組(2)，其中M=Fk－Gk，則有

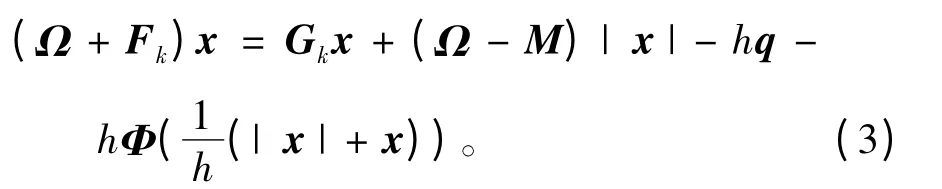
由這個改進的式子可得以下迭代算法。

算法1

1)初始向量x(0)∈Rn，置m=0;

2)對于k=1，2，…，l，在對應的處理器上分別求解

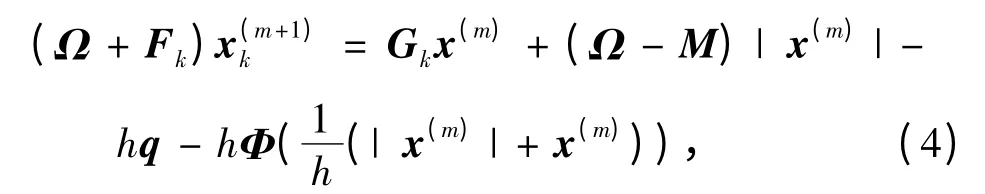
3)再將l個處理器的求解結果組合在一起，得

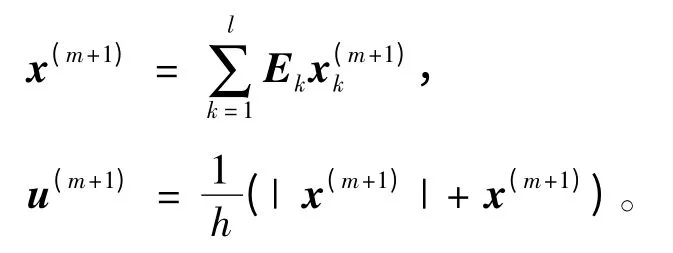
若u(m+1)滿足精度要求，則結束;若不滿足，則轉步驟2)繼續(xù)計算。

3 收斂分析

定理2 已知M為一個H+-矩陣，D=diag(M)，B=M－D，正對角矩陣Ω≥D，非線性項Φ(u)=(α1(u1)，α2(u2)，…，αn(un))T，滿足di＞。假設(Fk，Gk，Ek)(k=1，2，…，l;l≤n)為矩陣M的一個多分裂，且對于每個M=Fk－Gk為矩陣M的一個H-相容分裂，則對于任意初向量x(0)∈Rn，由算法1產生的迭代序列u(m{)收斂于弱非線性互補問題(1)的一個解u*。

設x*是準確解，則有

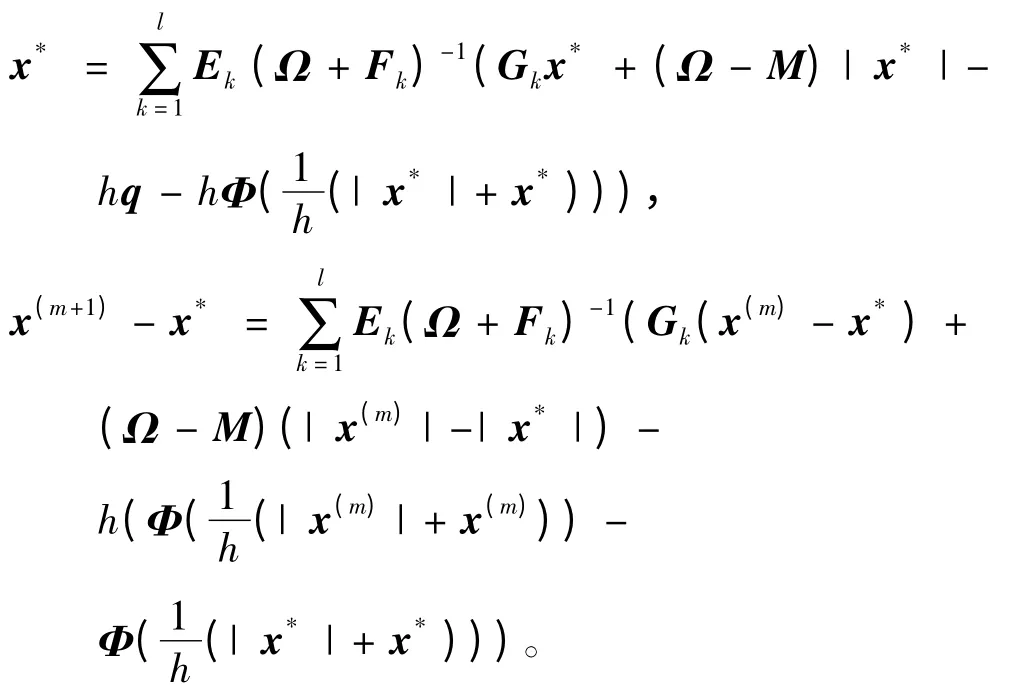
于是，

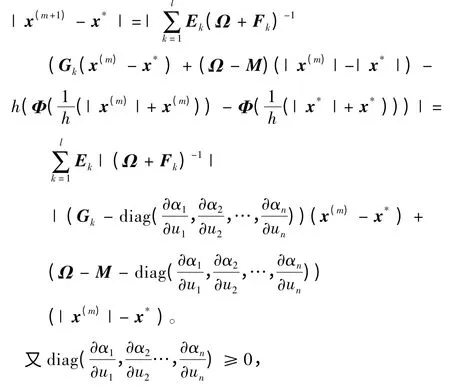
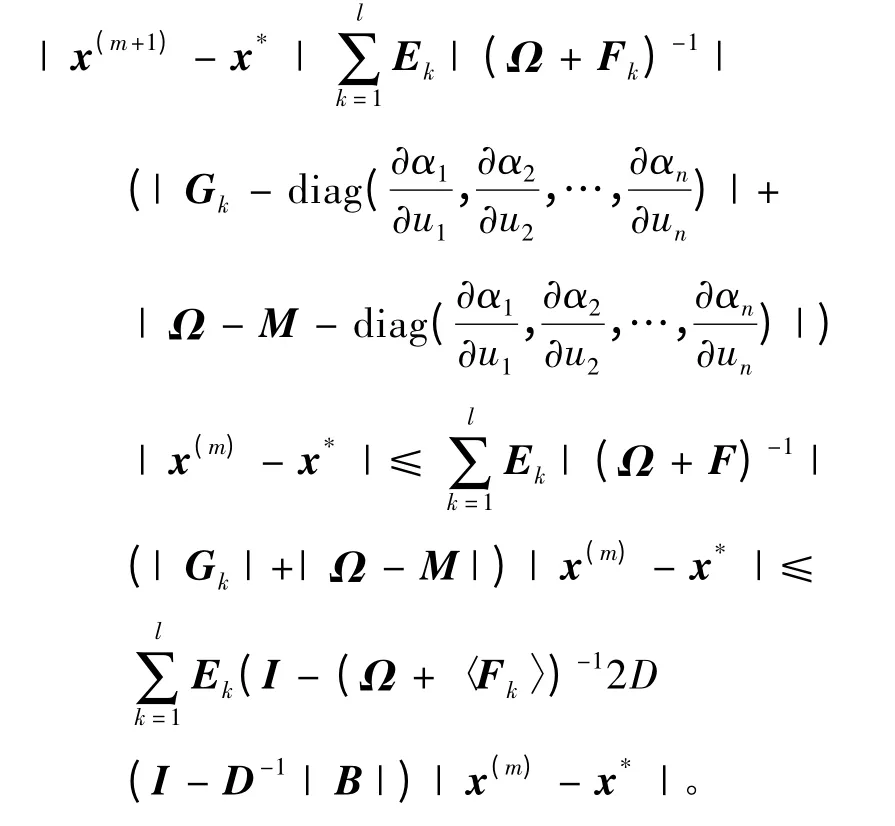
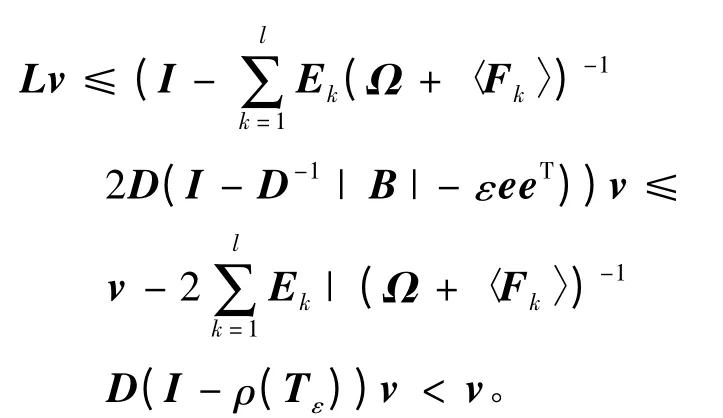
因此，ρ(L)＜1，由算法1產生的迭代序列，收斂到弱非線性互補問題的一個解u*。

4 數值例子

實驗在Matlab軟件環(huán)境中模擬，終止條件為:

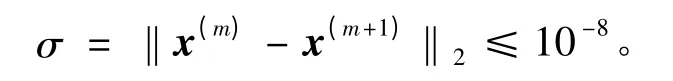
所有的初向量選擇為x(0)=(0，0，…，0)T∈Rn。

例1［7］考慮弱非線性互補問題(1)，設矩陣M∈Rn×n為一個H+-矩陣，且為對角塊矩陣，

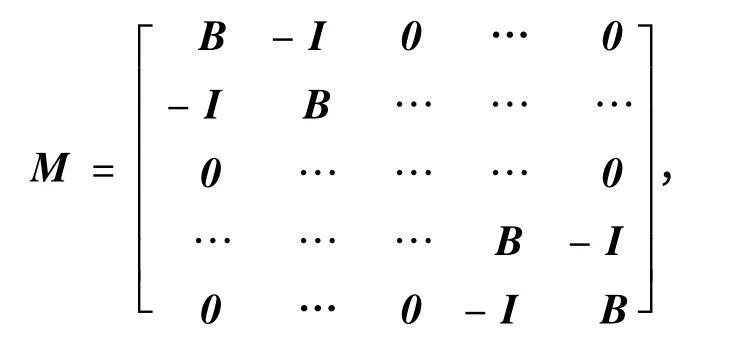
矩陣B為一個三對角線矩陣

q=(1，－1，…，1，－1)T，為單位矩陣。

模系矩陣多分裂迭代法的實驗結果如表1所示。m∈Z+滿足n=m2，n為矩陣M的階數;d為迭代步數;t為迭代時間。從實驗結果可看出，模系多分裂迭代法的迭代速度快，迭代步數少，實驗結果較理想。

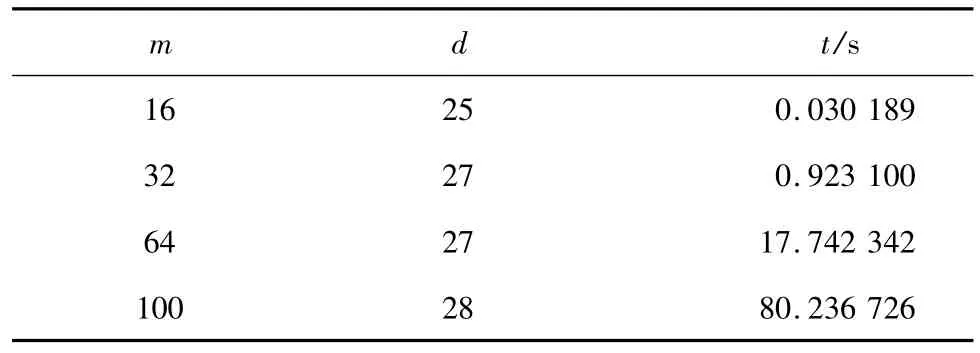
表1 模系矩陣多分裂迭代法的實驗結果Tab.1 Experimental results of MSMGS iterative method

5 結束語

運用矩陣多重分裂理論，結合Bai Zhongzhi［1-2］提出的一類模系分裂迭代算法，給出了一類求解弱非線性互補問題的模系矩陣多分裂迭代算法，并分析了算法的收斂性。數值例子說明算法的有效性。

［1］Bai Zhongzhi.Modulus-based matrix splitting iteration methods for linear complementarity problems［J］.Numerical Linear Algebra with Applications，2009，17(6):917-933.

［2］Bai Zhongzhi，Zhang Lili.Modulus-based synchronous multisplitting iteration methods for linear complementarity problems［J］.Numerical Linear Algebra with Applications，2013，20(3):425-439.

［3］張麗麗.關于線性互補問題的模系矩陣分裂迭代方法［J］.計算數學，2012，34(4):373-386.

［4］Li Chenliang，Zeng Jinping.A mutisplitting and additive Schwarz iteration scheme for solving nonlinear complementarity problems［J］.Journal of Numerical Methods and Computer Applications，2003，24(4):268-275.

［5］Noor M A.Fixed point approach for complementarity problems［J］.Journal of Mathematical Analysis and Applications，1988，133(2):437-448.

［6］Bai Zhongzhi，Evans D J.Chaotic iterative methods for the linear complementarity problems［J］.Journal of Computational and Applied Mathematics，1998，96(2):127-138.

［7］Frommer A，Mayer G.On the theory and practice of multisplitting methods in parallel computation［J］.Computing，1992，49(1):63-74.

［8］Mangasarian O L.Solution of symmetric linear complementarity problems by iterative methods［J］.Journal of Optimization Theory and Applications，1977，22(4):465-485.