大視場星敏感器標定技術*

李勉洪，丁國鵬，鄭偉波

(中國科學院 上海技術物理研究所，上海200083)

0 引 言

星敏感器是以恒星為參照物的高精度空間姿態測量裝置，它通過探測識別天球坐標系中恒星來確定衛星、導彈等航空航天飛行器相對于慣性坐標系的三軸姿態，具有重要的應用價值。目前，星敏感器正沿著高可靠性、小型一體化、自主、大視場、高數據更新率、高精度的方向發展［1］。單星測角精度是星敏感器整體精度的基礎，它直接影響姿態角測量精度。大視場光學系統會引入的非線性畸變，隨著星敏感器的視場角增大，將會影響其測量精度。另外，加工裝配誤差使得探測器平面存在傾斜旋轉，這將導致圖像出現傾斜畸變，從而影響星敏感器的測量精度。因此，必須對于大視場星敏感器進行標定，實現畸變校正，以便提高星敏感器整體測量精度。

目前，通常采用畸變模型法［2］及其改進方法，比如:分區線性畸變模型校正［3］實現畸變校正，或者通過直接映射法［4］進行畸變校正。但是大視場光學系統的畸變無法準確進行數學建模，精度要求越高，模型越復雜，參數越多，位置變換關系越復雜，不適合實時計算。而隨著視場角和探測器分辨率的增大，直接映射法需要建立龐大的位置映射表，而采用細分法進行亞像元質心定位后，其映射表將變得更大，不適用于嵌入式系統。對此，本文提出一種基于遺傳算法優化的BP 神經網絡算法進行大視場星敏感器的標定方法，利用BP 神經網絡的泛化能力表達復雜的非線性畸變模型，再通過遺傳算法優化克服BP 神經網絡局部優化的缺陷。

1 星敏感器標定原理

1.1 單星成像模型

空間物體到相機成像平面的成像過程通常可以看作是一個中心投影的過程，一般使用針孔成像模型來描述，如圖1所示。圖中Oc為投影中心，在攝像機模型中稱為光心，其到成像平面π 的距離f 稱為焦距。過點Oc垂直成像平面π 的直線稱為主軸，其與成像平面的交點Os稱為主點。空間恒星Pc與光心Oc的連線與成像平面的交點Ps即為該恒星在成像平面所成的像。

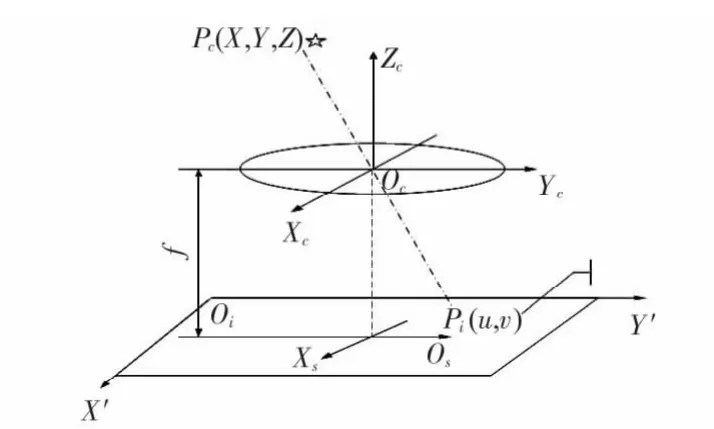
圖1 星敏感器成像原理圖Fig 1 Imaging principle of star sensor

根據上述投影模型建立攝像機坐標系OcXcYcZc，成像平面坐標系OsXsYs以及計算機圖像坐標系OiXiYi，假設恒星P 在該坐標系下的單位向量為Pc=［X，Y，Z］，其在成像平面所成的像在圖像坐標系下通過質心定位獲得的坐標記為Pi=［u，v］，單位為像素(pixel)，主點Os在圖像坐標系的坐標記為Po=［u0，v0］，則可以建立如下投影關系的數學描述

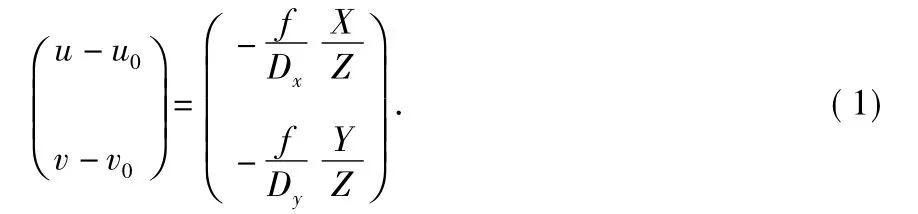
其中，Dx，Dy分別為探測器像元的高和寬。

1.2 單星測角原理

圖2 所示為單星測角系統。

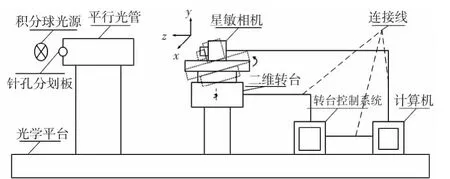
圖2 單星測角系統Fig 2 Single star angle measurement system

該系統在測量過程中使用了高精度的二維轉臺(精度為0.001°)，把大視場星敏相機固定在二維轉臺上，積分球光源通過針孔分劃板的光被平行光管準直后形成的平行星光在相機成像平面的主點位置產生星點像。轉動二維轉臺，記下此時二維轉臺的旋轉角度值為［ωx，ωy］，則由坐標系旋轉矩陣可以獲得平行光管產生的星點目標在攝像機坐標系的單位向量為

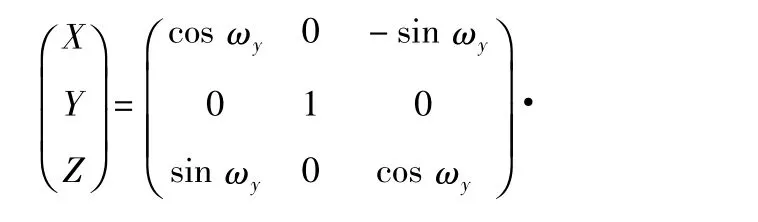
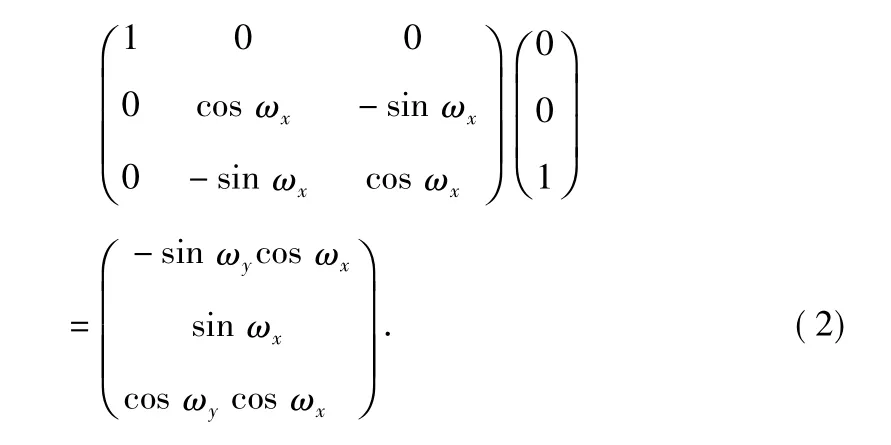
由式(1)和式(2)可以獲得星點像坐標與轉臺角位置的關系

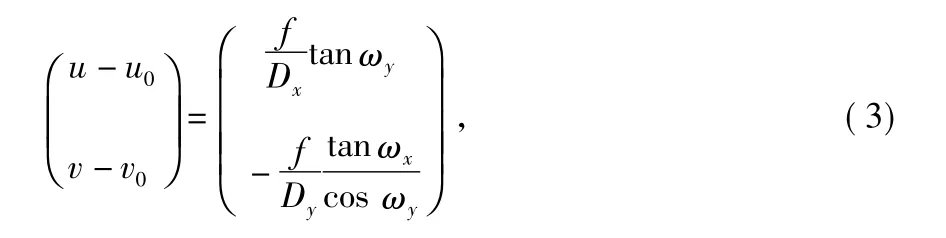
則根據星點像質心位置，可以反推得出二維轉臺的角位置

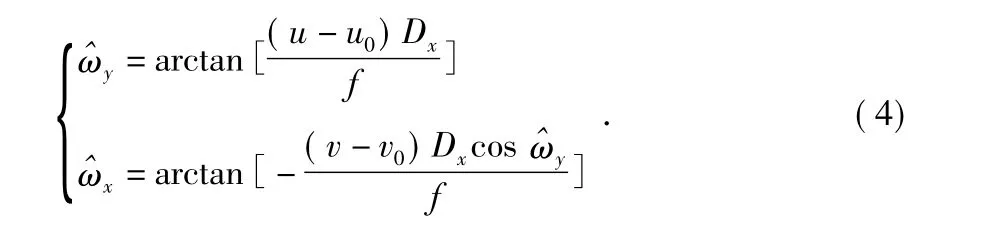
1.3 標定原理

星敏感器光學系統存在不同程度的幾何畸變，視場越大，畸變程度越嚴重。另外由于存在加工誤差和裝配誤差，探測器成像平面與光學系統的光軸并不嚴格垂直，探測器成像平面與理想安裝方式有一個旋轉角度，成像平面主點位置發生偏移，這些因素都將導致實際星像點的質心位置P'i=［u'，v'］與理想星像點質心位置Pi=［u，v］并不重合，從而引入測角誤差，影響星敏感器精度。

星敏感器的標定原理是通過一些已知的參考點，即無失真圖像中某些星像點質心位置和畸變圖像相應星像點質心位置間對應關系，建立起整個圖像中畸變坐標與理想坐標之間的映射關系，從而達到標定的目的。

鑒于星敏感器畸變模型無法準確建模以及直接映射法在大視場和大分辨率圖像的應用場景下數據量龐大的缺陷，本文采用BP 神經網絡來表達星敏感器畸變這一非線性系統，并通過遺傳算法優化BP 神經網絡，從而實現大視場星敏感器的標定。

2 標定方法與關鍵算法

2.1 BP 神經網絡模型

BP 神經網絡是一種多層前饋神經網絡，其網絡拓撲結構如圖3 所示。其中，ai，bk為神經網絡閾值，wij，wik為神經網絡權值。從圖3 可以看出:BP 神經網絡可以看成一個非線性函數，神經網絡權值和閾值為該函數的參數。輸入信號從輸入層經隱含層逐層處理直至輸出層，如果輸出層得不到期望輸出，則反向傳播，根據誤差調整網絡的權值和閾值，從而使BP 神經網絡不斷逼近期望輸出。

圖3 BP 神經網絡拓撲圖Fig 3 Topological diagram of BP neural network

2.2 獲取神經網絡訓練樣本集

假設星敏相機的視場角為θx×θy，其中，θx為水平視場角，θy為垂直視場角;圖像尺寸為M×N，焦距為f，采用圖2所示的測角系統，將星敏相機固定于二維轉臺上，保證相機光軸于平行光管光軸，采集圖像并獲得星像點的位置坐標為C00=［x00，y00］，分別以Δθx和Δθy的角度增量在相機視場范圍內旋轉二維轉臺X 方向和Y 方向，則可以得到二維轉臺在視場范圍內的角位置為

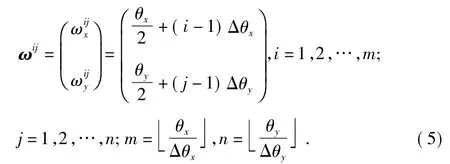
在上述二維轉臺的每個角位置獲取圖像并通過文獻［5］所述質心定位算法獲得對應星像點sij的坐標位置

其中，xij和yij分別為圖像平面的行坐標和列坐標。

根據以下公式

構造畸變樣本集合

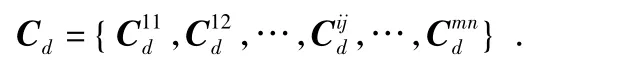
根據公式(3)可以獲得星像點Sij對應的理想成像坐標記為由此構造期望輸出理想樣本集Cu=。根據式(8)采用最大最小法歸一化Cd，Cu得到歸一化的輸入樣本集和對應的輸出樣本集

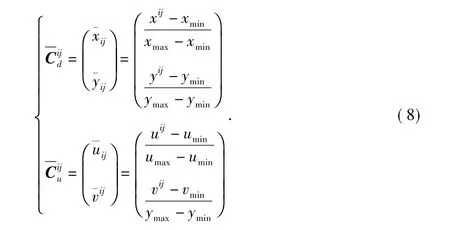
其中

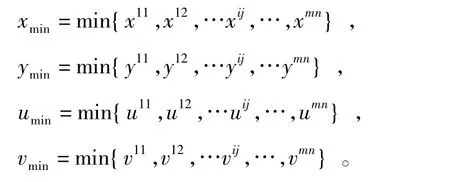
2.3 遺傳算法優化BP 神經網絡算法

BP 神經網絡是以梯度下降法為基礎的非線性優化方法，不可避免存在局部極小問題。而且實際問題的求解空間往往是極其復雜的多維曲面，存在許多局部極小點，更使網絡陷入局部極小點的可能性增加，采用隨機初始化神經網絡的權值和閾值的方法很難使得網絡訓練達到全局最優［6］。本文采用遺傳算法對BP 神經網絡進行優化，通過遺傳算法得到更好的網絡初始權值和閾值，其基本思想就是利用個體代表網絡的初始權值和閾值，通過遺傳操作尋找最優個體作為BP 神經網絡的最優初始權值和閾值。具體操作步驟如下:

1)確定神經網絡拓撲結構，采用三層BP 神經網絡，輸入層節點數p=2，輸出層節點數q=2，隱含層節點數l ＜，其中，a 為0～10 之間的常數，輸入層和隱含層的節點轉移函數采用log－sigmoid 函數，輸出層節點轉移函數采用線性函數。

2)通過遺傳算法優化BP 神經網絡的初始權值和閾值。遺傳算法的基本要素包括染色體編碼方法、適應度函數、選擇、交叉和變異等遺傳操作以及運行參數。

本文采用實數串編碼方式，每個個體均用一個實數串表示，由輸入層與隱含層連接權值、隱含層閾值、隱含層與輸出層連接權值和輸出層閾值4 部分組成，第i 個個體ai表示為{ai1，ai2，…，ain}其中，n=(p+q+1)×l+q，i=1，2，…，N，N 為種群規模。

采用神經網絡預測誤差大于某個閾值的比例作為個體的適應度值，即將每個個體作為BP 神經網絡初始權值和閾值，用訓練樣本集進行初步訓練，得到的預測誤差大于某個閾值的比例作為個體適應度，個體適應度越小，個體越優。

采用實數交叉，第k 個染色體ak和第l 個染色體al在j 位的交叉操作方法如下

其中，b 為0 ～1 之間的隨機數。

變異操作，選取第i 個個體的第j 個基因aij進行變異，變異操作如下

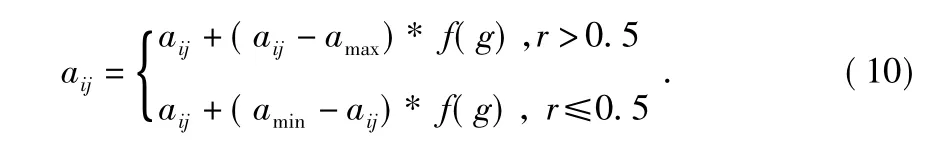
其中，amax為基因aij的上界，amin為基因aij的下界，f(g)=r2(1－g/Gmax)2，r2為一個隨機數，g 為當前迭代次數，Gmax為最大進化次數，r 為0 ～1 之間的隨機數。

遺傳算法優化的具體步驟如下:

a.設置種群規模、進化次數、交叉概率以及變異概率;并在初始化范圍內初始化每個個體，并計算每個個體的適應度;

b.進行選擇、交叉和變異操作獲得新一代種群，計算該種群每個個體的適應度，從中找出最優個體并替換最差個體;

c.判斷是否達到終止條件，即進化次數是否結束，若不是，則返回上一步;

d.將最優個體的實數編碼保存下來，作為下步神經網絡訓練的初始權值和閾值。

3)訓練BP 神經網絡，設置最大訓練次數，學習速率和最大誤差平方和，在每一輪迭代中，分別取訓練樣本集中畸變坐標樣本作為神經網絡輸入，計算神經網絡輸出向量Oij，并與對應的理想輸出樣本比較。將比較誤差用于調節神經網絡連接權值和閾值，反復訓練神經網絡，直到滿足終止條件，即到達迭代次數或者誤差滿足要求，保存該神經網絡的結構和模型參數。

4)獲得不同隱含層節點數下的神經網絡結構及其模型參數，比較誤差，保存最優的神經網絡和模型參數作為最終畸變校正的模型。

3 實驗與結果

實驗用星敏感器的具體參數如表1 所示。

表1 星敏感器參數Tab 1 Parameters of star sensor

根據2.1 小節所述采集獲得神經網絡訓練樣本集，其中Δθx=Δθy=1°，共獲得個4 870 個有效樣本。其對比圖如圖4 所示。

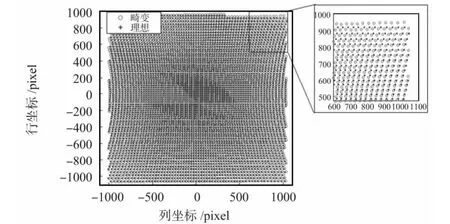
圖4 畸變坐標和理想坐標對比圖Fig 4 Comparison of distorted coordinates and ideal coordinates

根據上述訓練樣本訓練遺傳算法優化的BP 神經網絡，設置BP 神經網絡最大訓練次數為800，學習速率η=0.01，允許最大誤差平方和為ε=0.001，設置遺傳算法種群規模為15，進化次數為50，交叉概率為0.3，變異概率為0.2，訓練得出神經網絡結構參數，進行坐標畸變校正。可以得到校正坐標和理想坐標的對比圖如圖5 所示。

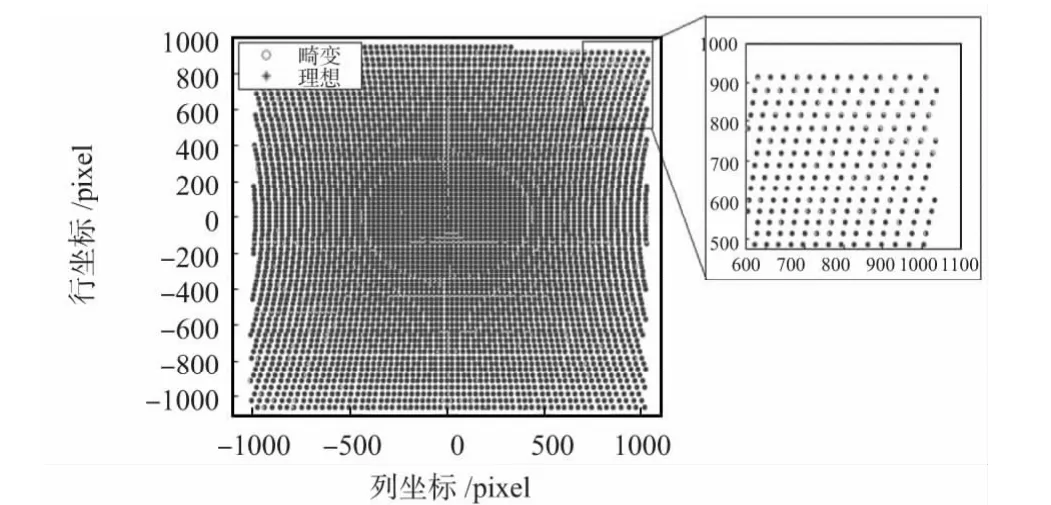
圖5 校正坐標與理想坐標對比圖Fig 5 Comparison of calibrated coordinates and ideal coordinates

在與訓練樣本集不同的轉臺角位置獲取測試樣本集進行校正，并與文獻［7］中所述的分區擬合方法進行比較，計算后誤差分析如表2 所示。

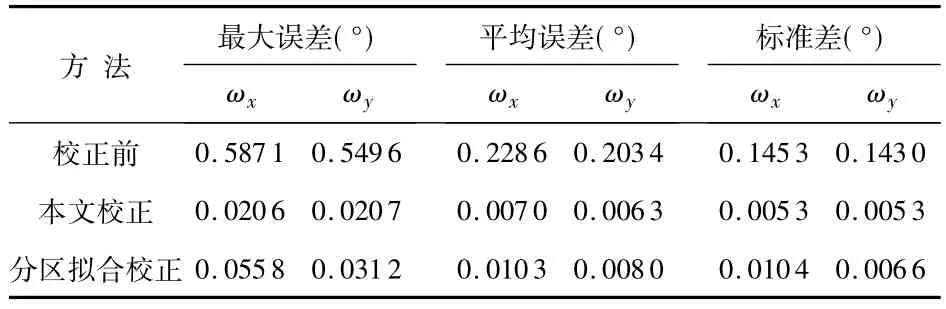
表2 誤差分析Tab 2 Error analysis

假設分區整體擬合法將整個視場分為M×N 個區域，則擬合所得的參數個數為6×M×N，另外還需要M+N 個輔助參數，則總共有M+N+6MN 個參數，本實驗采用M=N=3 的分區參數，則總共有60 個參數。而本文方法需要5l+2 個神經網絡模型參數，其中，l 為隱含層節點數，取值范圍為2 ～12，另外需要10 個輔助參數，本實驗中l=9，因此，總共需要57 個參數。

而由表2 可以得出，遺傳算法優化BP 神經網絡算法的平均絕對誤差和最大絕對誤差相比分區整體擬合法均有所降低，在所需參數相近的情況下，精度比分區整體擬合法提高將近1 倍，這說明本文提出的大視場星敏畸變校正方法是一種有效的方法。

4 結 論

本文分析了影響星敏感器測角精度的因素，建立了大視場星敏感器標定系統，提出使用BP 神經網絡表達大視場星敏感器畸變這一非線性模型，并采用遺傳算法優化BP神經網絡，克服其容易陷入局部優化的缺陷。實驗結果表明:本文提出的標定方法精度高，使得單星測角誤差由標定前的0.14°降低到0.0053°，測角精度提高將近30 倍，并且效率高，穩定性好。

［1］ 孫高飛，張國玉，鄭 茹，等.星敏感器標定方法的研究現狀與發展趨勢［J］.長春理工大學學報:自然科學版，2010，33(4):8－14.

［2］ 楊比武，郭曉松.攝像機鏡頭非線性畸變校正方法綜述［J］.中國圖像圖形學報，2005，10(3):269－274.

［3］ 劉力雙，孫雙花，呂乃光，等.一種圖像測量系統的現場標定和畸變校正方法［J］.傳感器與微系統，2008，27(5):66－68.

［4］ 鄧 雷，龔惠興.一種實用廣角成像系統幾何畸變數字實時校正方法［J］.紅外技術，2006，28(10):571－575.

［5］ 李玉峰，郝志航.星點圖像超精度亞像元細分定位算法的研究［J］.光學技術，2005，31(5):666－668.

［6］ 秦慶兵.基于神經網絡的攝像機畸變校正研究［D］.沈陽: 東北大學，2010.

［7］ 喬培玉，何 昕，魏仲慧，等.高精度星敏感器的標定［J］.紅外與激光工程，2012，41(10):2779－2784.