基于RSSI的KNN—PIT室內自適應定位算法*

唐 瑞， 孫冰潔， 周禮爭， 余 敏

(1.江西師范大學 軟件學院，江西 南昌 330022； 2.江西師范大學 計算機信息工程學院，江西 南昌 330022)

基于RSSI的KNN—PIT室內自適應定位算法*

唐 瑞1， 孫冰潔1， 周禮爭2， 余 敏2

(1.江西師范大學 軟件學院，江西 南昌 330022； 2.江西師范大學 計算機信息工程學院，江西 南昌 330022)

針對基于接收信號強度指示(RSSI)的K最近鄰(KNN)算法在室內定位精度較低的問題，提出一種改進的KNN—三角形內點(KNN—PIT)室內定位算法。根據室內空間結構特征，建立具有類標號的位置指紋庫。引入虛擬參考點，利用PIT原理進一步約束目標點的定位區域，自適應地使用定位算法進行定位。綜合運用高斯濾波、均值濾波技術，降低離線和在線階段的信號隨機誤差。結果表明：改進后的KNN—PIT定位算法可以更好地估計用戶的實際位置，降低定位誤差，定位精度提高12.5 %。

室內定位； K最近鄰； 三角形內點； 虛擬參考點； 自適應

0 引 言

隨著通信技術的發展，全球定位系統(global positioning system，GPS)已成為室外導航定位中的主要技術。但是，在人類活動密集的地方，如,大型購物中心、辦公樓、圖書館等復雜環境中，GPS因信號受干擾、遮擋等不能精確定位。基于接收信號強度指示(received signal strength indication，RSSI)的室內定位技術成為研究的熱點[1,2]。目前研究的熱點包括如何降低離線指紋庫采集的工作量、減少在線匹配的復雜度、改進算法提高定位實時性與準確性[3,4]。

文獻[5]指出K最近鄰(K-nearest neighbor，KNN)算法中K參數的改變與定位精度不存在單一的正比例關系；文獻[6]提出表征點位幾何特性的點散發性強度概念，并利用該強度值動態地選擇KNN參數K；文獻[7]用主成分分析(principal component analysis，PCA)和最小二乘支持向量回歸機(least square support vector regression，LSSVR)實現數據降維和位置回歸預測；文獻[8]結合煤礦井下環境提出一種自適應RSSI三角質心定位算法；文獻[9]研究了RSSI值與幾何距離的關系，提出了一種基于特征尺度的KNN。

由于RSSI受到多徑效應、陰影效應等的影響，本文在離線階段，對樣本數據進行高斯濾波，獲得表征較為真實的位置指紋數據，在線階段使用均值濾波降低實時采樣RSSI帶來的較大誤差。利用最佳三角形內點 (point in triangulation，PIT) 測試法和虛擬點進一步約束定位點的所屬區域，提出KNN—PIT算法，自適應地使用定位算法進行定位。

1 具有類標號的位置指紋庫構建

基于RSSI位置指紋的室內定位方法分為離線信號采集構建指紋庫階段和在線實時定位兩個階段。離線階段，在待定位區域建立平面坐標系并劃分網格，以網格點作為參考點(reference point，RP)。在各RP上采集周邊各接入點(access point，AP)的RSSI，建立各個參考點對應的位置和信號強度的關系，即位置指紋庫。

具有類標號的位置指紋庫在傳統指紋庫中添加新的屬性，即類標簽。根據室內的空間結構特征，將各區域的RP歸為一類，位置指紋庫如表1所示。

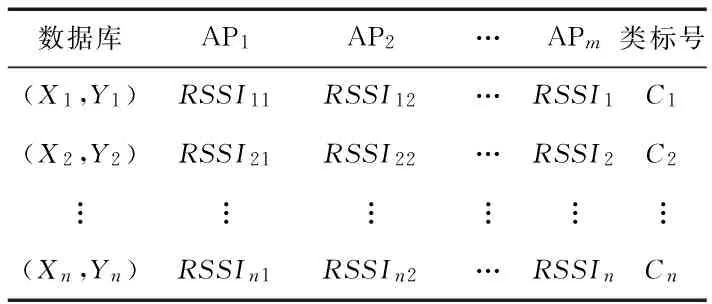
表1 具有類標號的指紋庫

位置指紋集為S={(L1,R1,C1),(L2,R2,C2),…,(Ln,Rn,Cn),Rn={RSSIn1,RSSIn2,…,RSSInm}∈Rm,Cn∈{1,2,…,j)，其中,Ln=(xn,yn)表示參考點n的二維位置坐標,RSSInm表示參考點n處接收第m個AP的信號強度值,Cn表示參考點n的類標號，取值為1～j。

2 KNN與PIT原理

KNN定位算法首先計算定位點處測得的RSSI向量與各RP點測得的RSSI向量的余弦相似度。兩向量的余弦相似度如下所示

(1)

然后在位置指紋庫中尋找最接近的k個RSSI向量。由于指紋庫中每個RSSI向量唯一對應一個參考點的二維坐標。最終定位點的位置估計為k個參考點二維坐標的加權值，第i個參考點的權值為wi

(2)

其中，si為第i個參考點與定位點的空間相似度。最終定位點的位置估計為

(3)

PIT原理如圖1所示。當存在一個方向，節點T沿著這個方向移動會同時遠離或接近三角形頂點A,B和C，判定該節點不在三角形內;否則,判定該節點在三角形內。

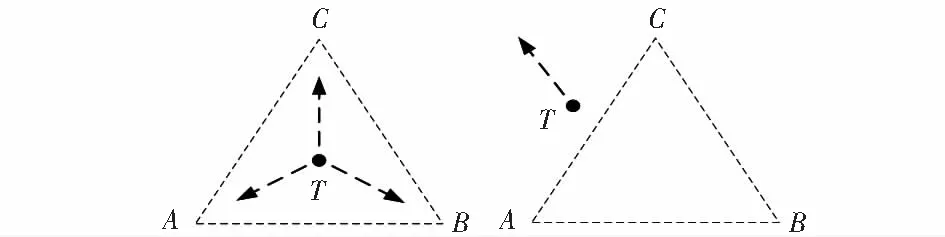
圖1 PIT原理

目前數學理論上還有面積法、內角和法、同向法等判定一點T是否在三角形ABC中。本文采用面積法定性的判斷定位點是否在三角形內，使用空間向量之間的距離代替指紋點之間的距離。

設三角形頂點坐標A,B和C處的位置指紋為： (LA,RA,CA),(LB,RB,CB)和(LC,RC,CC)。定位點處的RSSI向量為RT,則

(4)

由秦九韶—海倫公式得三角形ABC的面積SABC為

(5)

同理，可計算SABT,SBCT和SACT，若SABC=SABT+SBCT+SACT，判定定位點在三角形ABC內;否則，判定定位點在三角形外。實際實驗時，由于存在信號的隨機誤差，假定滿足SABC-(SABT+SBCT+SACT)<δ，δ為設定的閾值，即認為點在三角形內。

3 自適應的KNN—PIT定位算法

根據無線信號傳播理論，當兩點比較近時，中間點處的RSSI可由兩點RSSI的均值近似代替，因此,可以添加虛擬參考點進一步約束定位點的所在區域，實現更精確的定位。但是，若參考點不在同一類時，表明中間有墻體阻隔，引入虛擬點可能帶來更大的定位誤差。同時，若k個參考點在同一直線上則無法構成三角形，因此，需要分類討論。

3.1KNN算法匹配前3個點屬同一類

如圖2所示，KNN匹配前3個參考點K1,K2,K3同類但不構成三角形，引入K4，且K4與原參考點屬于同一類。增加虛擬參考點P，P點處的RSSI由K1和K4的RSSI均值代替。通過面積法計算得定位點在三角形K1K2P內，則定位點T的位置估計為

(6)

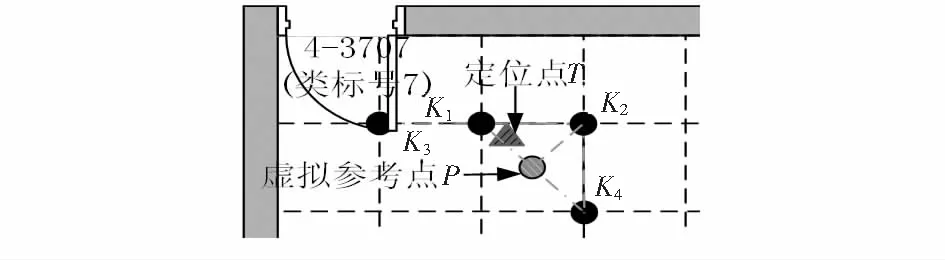
圖2 K1,K2,K3不構成三角形

如圖3所示，K1,K2和K3屬于同一類且構成三角形，通過面積法計算得定位點在三角形K1K2P內，則定位點T的位置估計由式(6)得出。

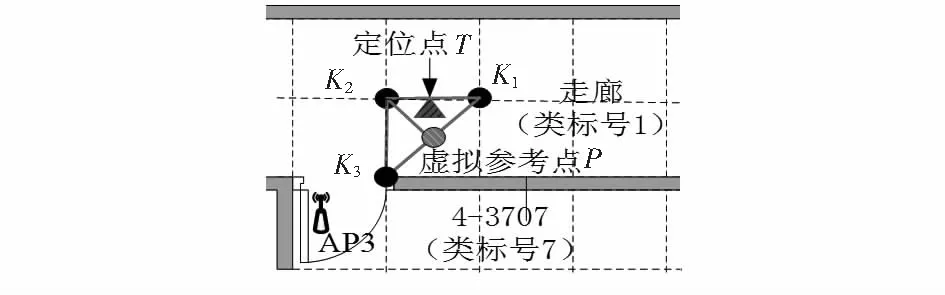
圖3 在未調整的三角形內

如圖4所示，K1,K2和K3屬于同一類且構成三角形，但定位點不在虛擬點P組成的三角形K1K2P和K2K3P內。引入K4參考點，通過面積法計算得定位點在三角形K1K4P內，則定位點T的位置估計為

(7)

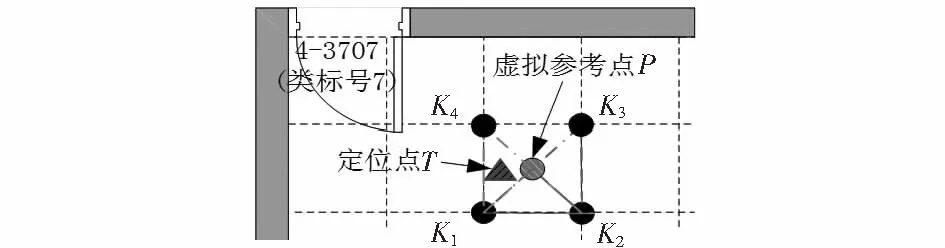
圖4 在調整后的三角形內

如圖5所示，K1,K2和K3屬于同一類且構成三角形，但定位點不在三角形K1K2P和K2K3P內，引入K4與原參考點不屬同一類，則定位點T的位置估計為

(8)

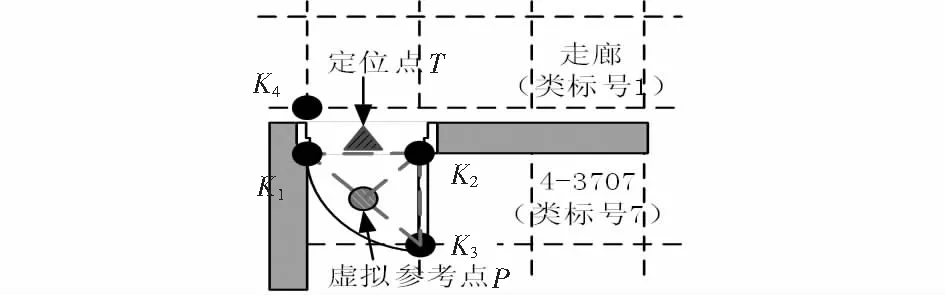
圖5 K1,K2,K3,K4不同類

3.2 KNN算法匹配前3個點不屬同一類

如圖6所示，K1,K2和K3不屬于同一類,則定位點T的位置估計由式(8)得出。

圖6 K1,K2,K3不同類

綜上，自適應的KNN—PIT定位模型如圖7所示。

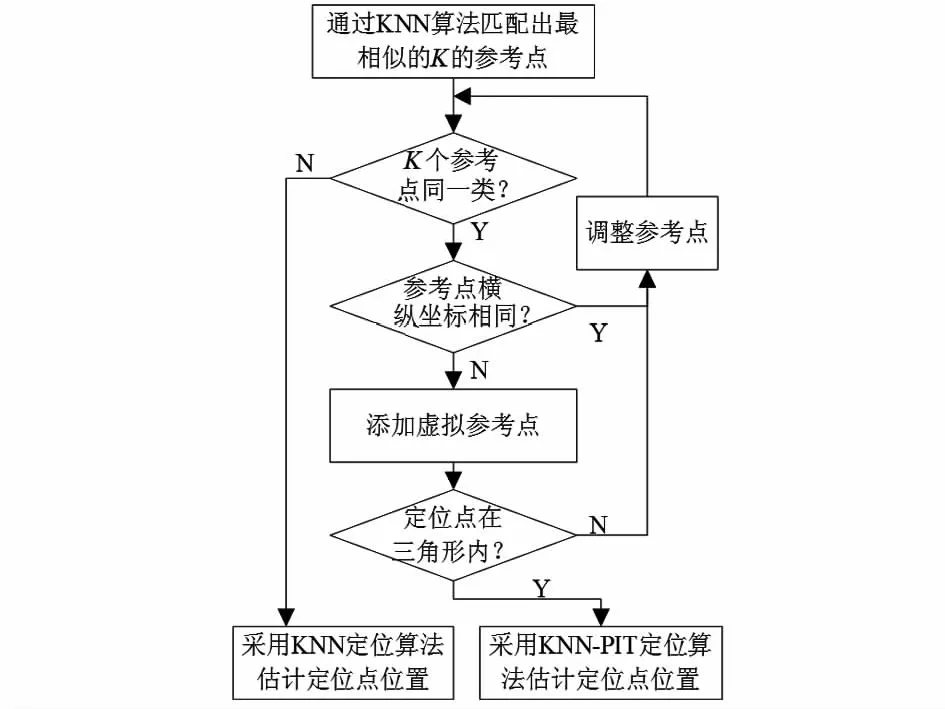
圖7 KNN—PIT定位模型

4 實驗與分析

為了檢測本文提出的KNN—PIT算法在室內的定位效果，實驗在先骕樓7樓進行。實驗環境的平面圖如圖8所示，參考點間距為2m，AP型號為TL—WR885N，移動采集終端為華為手機G606。

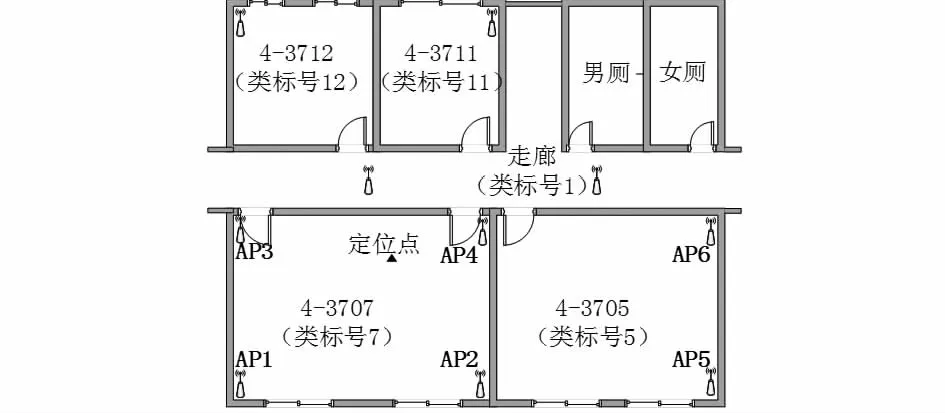
圖8 空間結構和AP的布局

為了降低RSSI不穩定的影響，各參考點采集各AP的RSSI值300次。通過大量實測數據分析，在某一點處測得某一AP的RSSI值整體呈正態分布，如圖9所示。

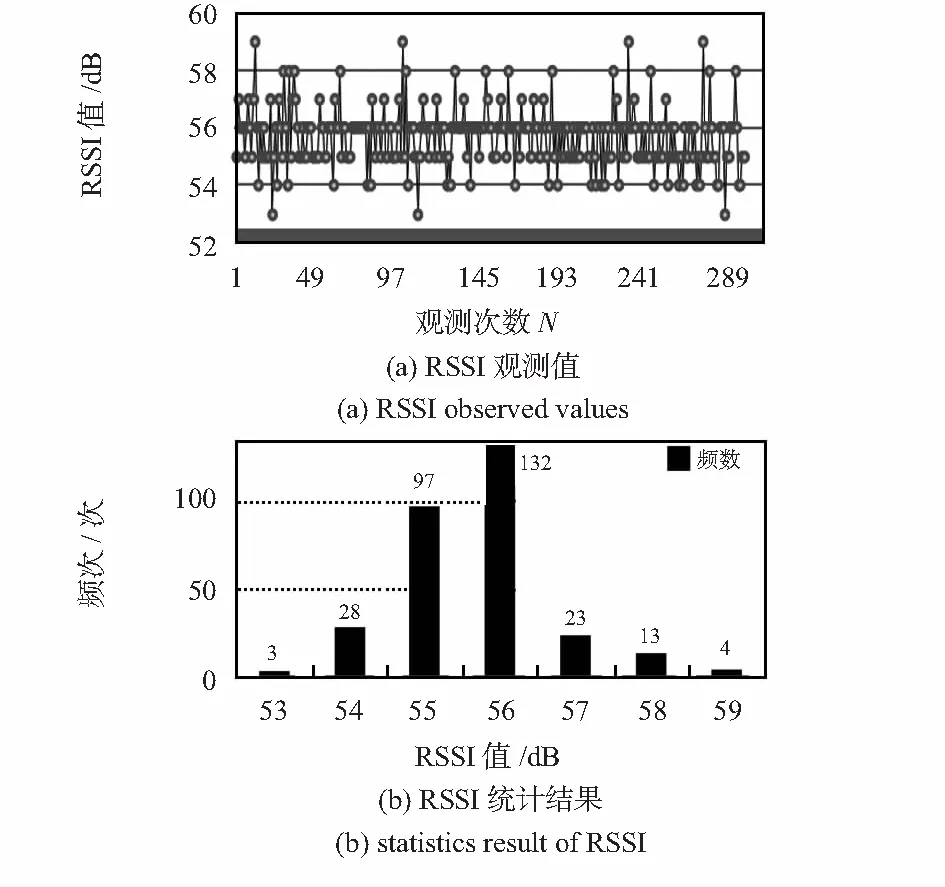
圖9 某點處采集某AP的RSSI值

本文離線階段采用高斯濾波技術，舍棄發生概率較低的數值，對高概率發生數值求均值，降低信號噪聲影響。在線階段使用均值濾波技術，將實時采集的若干次RSSI求均值作為實時RSSI，降低信號的隨機誤差。

考慮離線階段樣本采樣次數影響離線階段的工作量，也可能直接影響室內定位的精度。隨機以RSSI值采樣次數為30,60,90,120,150,180,210,240,270和300次進行對比實驗。實驗結果如圖10所示。

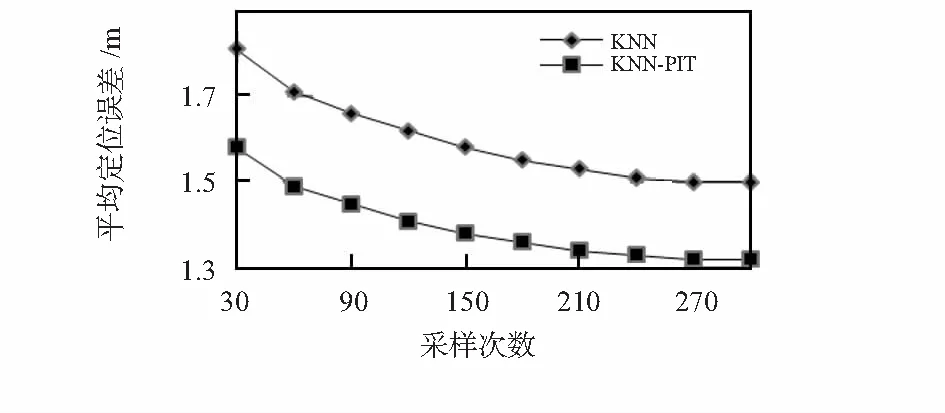
圖10 KNN和KNN—PIT算法對比

圖10表明:當位置指紋點采集的RSSI次數相同時，KNN—PIT算法在室內定位中具有更高的精度，定位精度平均提高12.5 %。

為了驗證在實時定位時均值濾波的效果和必要性，進行單次RSSI和3次RSSI作均值濾波處理對比實驗,每次定位誤差的實驗結果如圖11所示。

由圖11知，使用單次測得的RSSI進行定位，定位誤差波動性較大，而使用均值濾波技術后，定位誤差基本穩定在1.40m左右，標準差小，具有更好的適應性。

圖11 定位階段是否使用均值濾波技術的定位誤差

5 結 論

本文采用KNN—PIT算法進行室內定位，不僅有效降低了傳統KNN算法在室內定位的較大誤差，而且可以在不同環境下自適應地定位。實驗表明:改進后的算法具有更高的定位精度和可靠性。

[1]GuYanying,LoANiemegeersI.Asurveyofindoorpositioningsystemsforwirelesspersonalnetworks[J].CommunicationsSurveys&Tutorials,IEEE,2009,11(1):13-32.

[2]PrietoJ,MazuelasS,BahilloA,etal.Adaptivedatafusionforwirelesslocalizationinharshenvironments[J].IEEETransactionsonSignalProcessing,2012,60(4):1585-1596.

[3]JiangJoeAir,ZhengXiangyao,ChenYuan,etal.AdistributedRSS-basedlocalizationusingadynamiccircleexpandingmechanism[J].IEEESensorsJournal,2013,13(10):3754-3766.

[4] 花 超,吉小軍,蔡 萍,等.基于RSSI差分修正的加權質心定位算法[J].傳感器與微系統,2012,31(5):139-141.

[5]HonkavirtaV,PeralaT,Ali-LoyttyS,etal.AcomparativesurveyofWLANlocationfingerprintingmethods[C]∥WPNC2009,Hannover,Germany,2009:243- 251.

[6] 劉春燕,王 堅.基于幾何聚類指紋庫的約束KNN室內定位模型[J].武漢大學學報·信息科學版，2014,39(11):1287-1292.

[7] 張 勇,黃 杰,徐科宇.基于PCA-LSSVR算法的WLAN室內定位方法[J].儀器儀表學報,2015,36(2):408-414.

[8] 曹開來,余 敏.無線傳感器網絡煤礦井下RSSI自適應定位算法[J].傳感器與微系統,2014,33(6):129-132.

[9]LiDong,ZhangBaoxian,YaoZheng,etal.Afeaturescalingbasedk-Nearestneighboralgorithmforindoorpositioningsyste-m[C]∥GlobalCommunicationsConference,Austin,TX,2014:436-441.

Indoor adaptive KNN-PIT positioning algorithm based on RSSI*

TANG Rui1, SUN Bing-jie1, ZHOU Li-zheng2, YU Min2

(1.School of Software,Jiangxi Normal University,Nanchang 330022,China; 2.School of Computer Information and Engineering,Jiangxi Normal University,Nanchang 330022,China )

Aiming at problem of KNN algorithm low precision of indoor positioning based on RSSI,an improved KNN—PIT indoor positioning algorithm is put forward.According to structure feature of indoor space,establish location fingerprint database which has class labels.Introduce virtual reference points,use theory of PIT to further constrain localization area of target point,use positioning algorithm adaptively to carry out positioning. Comprehensively use Gauss filtering and mean filtering to reduce random errors of signal in online and offline stages.Results show that the improved KNN—PIT algorithm can better estimate the user’s actual location,and decrease significantly localization errors,positioning precision is improved by 12.5 %.

indoor positioning; K-nearest neighbor(KNN); point in triangulation(PIT); visual reference points; adaptive

10.13873/J.1000—9787(2015)07—0128—04

2015—05—11

國家自然科學基金資助項目(41374039)； 中國—波蘭國際科技合作項目(35—14)

TP 393

A

1000—9787(2015)07—0128—04

唐 瑞(1991-)，男，安徽合肥人，碩士研究生，主要研究方向為無線傳感器網絡、室內定位。