分區對接網格在跨流域氣體運動論統一算法的應用研究

吳俊林，彭傲平，李志輝，方 明

(中國空氣動力研究與發展中心超高速空氣動力研究所，四川綿陽 621000)

分區對接網格在跨流域氣體運動論統一算法的應用研究

吳俊林，彭傲平，李志輝*，方 明

(中國空氣動力研究與發展中心超高速空氣動力研究所，四川綿陽 621000)

為了模擬跨流域復雜物形繞流或多體流場，需要在位置空間建立能描述整個流場特性的網格系統，相應的數值計算方法也需要有所改進。本文采用分區對接網格處理復雜物形繞流或多體干擾流場，得到能準確描述流場特征的貼體網格系統。在此基礎上數值求解考慮轉動非平衡影響的Boltzmann-Rykov模型方程，在速度空間應用離散速度坐標法、位置空間采用數值差分NND格式。網格對接面上考慮分布函數的傳遞，包含網格點信息和網格點上速度的信息。通過計算得到復雜物形的流動特性。相關算例表明網格分區之間的流場參數光滑過渡。與文獻及DSMC結果的對比證實本文基于分區對接網格的氣體運動論統一算法是可靠的。

分區對接網格;統一算法;Rykov模型方程;多體流動

0 引言

氣體的宏觀流動本質上是由分子的微觀運動決定的，而描述微觀層次的基本方程是基于分子量子力學系統的Liouville方程及基于約化s粒子分布函數的BBGKY方程鏈，二者是等價的［1］。僅考慮二體碰撞，并作混沌假設得到Boltzmann方程［2］，它采用速度分布函數描述一個微觀體系的平均行為，嚴格意義上來說它屬于介觀層次的分子運動描述。其中速度分布函數f是空間位置r和速度v的連續平滑函數，它并不包含每個微觀分子的細致結構［1］。開展氣體動理學研究一般都是基于Boltzmann方程，并且經過學者不斷發展得到了多原子氣體、多組元混合氣體及化學反應混合氣體的分子輸運Boltzmann方程［1，3］。但由于它是一個高維多重積分的微分方程，且非線性碰撞項極其復雜，直接求解是很困難的［3-4］。比較廣泛采用的方法包括 Chapmann-Enskog逐級逼近解法［4］、模型方程方法［5］、有限差分Monte Carlo方法［6］及格子Boltzmann方法［7］。

最近十幾年以來，針對Boltzmann方程開展的研究工作再次成為國際上的熱點問題，基于模型方程的數值求解方法取得了極大進步。徐昆等發展了氣體運動BGK格式(GKS)求解高速粘性流動等問題［8］，為連續、近連續流動模擬提供了一種新的思路。李志輝發展離散速度坐標法求解Boltzmann模型方程［9］，在平板Couette流動［10］等問題中得到應用，并建立起基于HPF、MPI的并行算法用于三維繞流［11-12］。在解決實際問題中，為了模擬復雜物形繞流或多體流場，需要在位置空間建立能描述整個流場特性的網格系統。非結構網格雖然對復雜外形適應能力很強，但其計算效率相對較低［13］，技術處理和相應算法改進上難度較大。相比較而言，分區對接網格對于氣體運動論統一算法中的位置空間有限差分方法來說更容易實現。而且這種網格技術的對接面兩側網格點完全對接，避免了虛網格及流場信息的代數插值，既保證了對復雜外形的適應能力，又能較好地保證流動通量守恒［14］。

本文采用分塊對接網格系統處理二維復雜外形或多體流動問題，針對氣體運動論統一算法在速度空間的速度離散、位置空間的有限差分進行算法設計和技術處理，得到能夠描述多體干擾流動問題的跨流域算法程序，并驗證對接面兩側流場參數是否光滑過渡。

1 計算方法

1.1 控制方程

考慮轉動非平衡效應的二維Boltzmann-Rykov模型方程［15］無量綱形式［16］在速度空間離散成為各個離散速度坐標點上彼此獨立的若干方程組，并將位置空間坐標通過雅克比(Jacobian)矩陣變換到計算平面內，得到二維跨流域氣體運動論統一算法的控制方程形式為［17］:

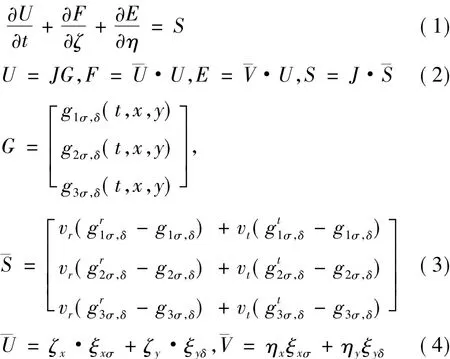
其中，σ=1，2，…，N1;δ=1，2，…，N2。g1、g2、g3是約化速度分布函數［17］，它是關于時間t，位置空間r和速度空間v的多維函數(對于二維問題具有五個自變量)。vt、vr分別是彈性碰撞頻率和非彈性碰撞頻率。

采用非定常時間分裂方法［9］，將控制方程(1)分裂為源項碰撞變化方程和位置空間的對流運動方程，得到求解約化速度分布函數方程的氣體運動論數值格式為:

其中，下標s表示源項，ζ、η為計算平面坐標。

時間上采用二階Runge-Kutta推進，位置空間采用NND-4(a)有限差分格式［18］。則該有限差分數值計算方法的穩定性條件為［19］:

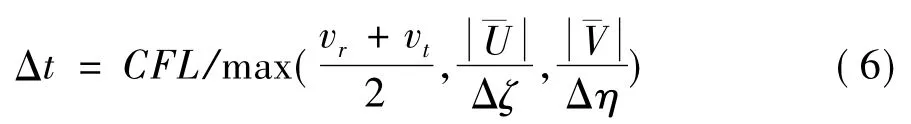
其中，CFL為時間步長調節系數，一般CFL＜1。

1.2 物面邊界條件

考慮轉動非平衡效應氣體運動論統一算法的物面邊界條件由分子與物面碰撞通量守恒無穿透條件［20］和平動、轉動能量平衡關系得到［21］:

2 分區對接網格算法

分區對接網格技術及其算法是數值模擬真實復雜流動的有效途徑。在分區流動計算中涉及兩個關鍵技術:一是邊界類型及分區相鄰關系判斷;二是鄰近分區之間信息的交換及流動信息在整個求解域中的傳播。

Qhw—第四系；J3-K1m—毛坦廠組(粗安斑巖、安山巖、安山質凝灰巖)；Pt3x—小溪河巖組(云母石英片巖、變粒巖)；DBG—大別巖群片麻巖組合；DBM—大別巖群大理巖組合；Pt3Tw—唐灣片麻巖體(二長花崗質片麻巖)；Pt3N—倪店片麻巖體(角閃二長質片麻巖)；Pt3L—龍眠片麻巖體(角閃斜長質片麻巖)；K1Xm—仙米尖單元(二長花崗巖)；K1H—華蓋山單元(石英正長斑巖)；K1D—大圓單元(角閃二長巖)；J3-K1Z—中義單元(石英二長巖)

由于流場采用固定網格劃分，網格不隨時間演變，因此在統一算法迭代之前的初始化過程中通過分區之間的位置關系判斷鄰近分區編號。判斷區域單元的每個邊界類型，如果是分區對接面則還需要給出鄰近分區內該對接面的網格序列號。

控制方程在每個分區中是獨立求解的，因此保證對接面兩側流場信息的正確傳遞是算法成功的關鍵。為了保證流場光滑過渡及流場信息在整個求解域內的正確傳遞，每個分區對接面網格的有限差分格式精度應該與內點保持一致，這就需要在對接面外設置虛擬網格，虛擬網格點的信息通過相鄰分區同一位置的值給出。值得注意的是分布函數G=G(t，r，v)是關于速度v的函數，因此虛擬網格點上速度方向在鄰近分區內對應的速度方向必須保持一致。虛擬網格點上的分布函數值可寫為:

其中border_i、border_j表示相鄰塊內該位置的網格點編號。

為了保證流場信息在分區對接面上的光滑過渡，需要對兩側分區分別迭代得到對接面上的分布函數值進行平均操作。物面和來流邊界的處理與單域網格一致［17］。

3 算例與討論

3.1 豎直平板繞流算例驗證

文獻［16］開展了稀薄過渡流區二維豎直平板高馬赫數繞流計算，本文以其為算例驗證分區對接網格的氣體運動論統一算法程序可靠性。計算區域及網格分區如圖1所示，豎直平板厚度不計，高為1。左端自由來流氮氣的無量綱速度［17］為S∞=7.0，壁面溫度Tw=10，努森數Kn∞=0.01。圖2給出了數值計算得到該高馬赫數豎直平板流場的無量綱壓力等值線分布，可以看到左端來流在平板前端形成一道脫體激波。各網格分區之間的流場參數實現了光滑過渡，說明對接面處理方法是合理的。流場信息在全求解域內實現了較好地傳遞。

圖1 豎直平板流場網格分區Fig.1 Multi-block patched mesh for flow past a erect plate

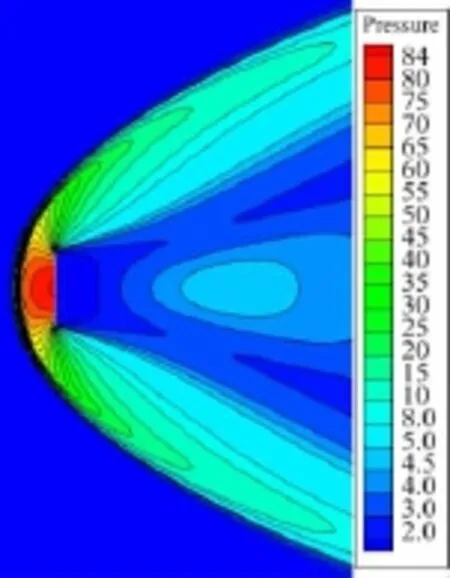
圖2 平板繞流壓力等值線Fig.2 Pressure contours of plate flow

圖3 平板繞流平動溫度等值線與文獻［16］的比較Fig.3 Translational temperature contours by GKUA compared with those from reference［16］

圖3 中基于分區對接網格的氣體運動論統一算法(GKUA)計算得到流場平動溫度分布與文獻［16］基本一致，包括脫體激波位置和形狀、等值線分布變化趨勢等。比較結果表明本文的分區對接網格實現是可靠的。此外，GKUA得到的流場等值線更加光滑，不會出現波浪式起伏現象，這是分區對接網格相比于單域網格的一大優勢。圖4中平板前端流場減速線上(y=0)的無量綱密度、平動溫度、轉動溫度分布與文獻的比較也很好地說明了分區對接網格在氣體運動論統一算法中實現過程的可靠性。

圖4 平板前端減速線上的流動參數分布Fig.4 Macro-parameter distribution on forepart decelerating line

3.2 Crookes輻射計對流問題［22］模擬驗證

將0.01 m×0.04 m的二維簡化Crookes輻射計模型置于0.44 m×0.44 m的方腔內，輻射計風向標左側溫度為450 K、右側為410 K，方腔壁溫固定為300 K。模型及流場分區網格如圖5所示。由于輻射計左右兩側以及方腔壁之間的溫差導致氣體對流運動。圖6給出了統一算法采用分區對接網格(圖5)計算得到該輻射計流場溫度分布與DSMC方法數值模擬結果的比較情況，可以看出二者能夠較好地在上下交界處匹配起來，尤其是近壁區域能完全重合。圖中DSMC方法的結果存在統計波動現象，而基于分區對接網格的統一算法(GKUA)等值線分布則較為光滑細膩，凸顯出后者在計算這種低速輻射對流問題方面的優越性。

圖5 Crookes輻射計模型及分區網格Fig.5 Model and multi-block patched mesh for Crookes vane

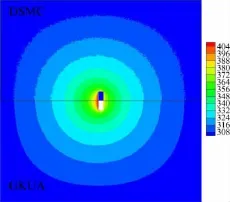
圖6 Crookes輻射計流場的溫度分布Fig.6 Temperature distribution around the vane

圖7 、圖8分別給出輻射計左側中心線、上半部分中心垂直線上的無量綱溫度和密度分布比較。可以看出DSMC和統一算法(GKUA)的計算結果沿這兩條線的流場參數輪廓線完全重合，進一步驗證了分區對接網格在統一算法中的實現是可靠的。

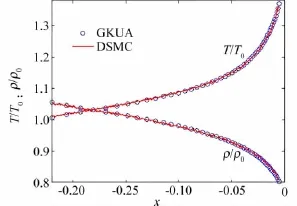
圖7 輻射計左側中心線上的溫度與密度分布Fig.7 Temperature and density distribution along the central line at the left side of the vane

圖8 輻射計上側中心垂直線上的溫度與密度分布Fig.8 Temperature and density distribution along the central vertical line above the vane

3.3 高馬赫數多體干擾復雜流動計算

流場中存在多個物體的情況需要采用分區對接網格才能描述。本文以相互交錯放置的兩個長方形為算例開展高馬赫數(Ma∞=6)多體流場計算。來流克努森數為Kn∞=0.003 65(對應近連續流區)，來流溫度T∞=273.15 K，設置壁面溫度為Tw=300 K，流動氣體為單原子氬氣Ar。圖9給出了兩個長方形的相對位置及流場網格劃分，其中長方形無量綱寬度為1，長度為5，左右交錯1，上下距離為2。

圖9 兩個長方形流場網格Fig.9 Mesh system for flow with two rectangles

圖10 -圖12是該多體干擾流場的馬赫數、無量綱溫度和壓力等值線云圖。可以看到整個流場在各網格分區之間光滑過渡，流場特征明顯且合理，證明分區對接網格在氣體運動論統一算法中的實現是正確的，分區對接面的處理是合理有效的。該多體干擾流場表現出連續流區的流動特征:物體前端出現脫體激波，使得超聲速來流跨越激波成為亞聲速流動。波后是高溫高壓區，延續到兩個交錯長方形的位置，最大無量綱溫度和壓力值分別達到13.5和55。脫體激波的形狀不規則，下方要“胖”一些。

脫體激波波后的高溫高壓低速氣體進入兩個長方形之間的槽道流動中。在向右運動過程中壓力溫度逐漸減小，速度逐漸恢復。特別是在槽道的核心區位置是典型的連續流區亞聲速槽道流動特征。槽道中的氣體在長方形后端的擴張作用與外場氣體壓縮的共同作用下，形成了一片類似于“噴管擴張段”的核心區，該核心區內氣體馬赫數重新達到并超過1，最高時馬赫數恢復到5左右，而壓力和速度持續降低，并且形成了上下兩道不太對稱的壓縮波。

從圖12中兩個長方形上下物面附近的壓力等值線分布能夠明顯看到一層薄薄的邊界層，邊界層厚度很小，這正是連續流動的典型特征。

圖10 兩個長方形流場馬赫數等值線云圖Fig.10 Mach number contours for flow with two rectangles

圖11 兩個長方形流場溫度等值線云圖Fig.11 Temperature contours for flow with two rectangles

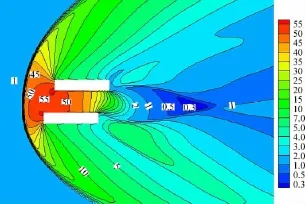
圖12 兩個長方形流場壓力等值線云圖Fig.12 Pressure contours for flow with two rectangles

此外，本文還數值計算了稀薄流區(Kn∞=1.0)上下對稱尖劈外形(如圖13所示)的復雜流動。來流馬赫數Ma∞=3，流動氣體為氮氣N2。圖14給出了該對稱尖劈流場的無量綱密度等值線云圖。不僅實現了分區之間流場參數的光滑過渡，高稀薄流動特征也非常明顯。壁面干擾在流場中影響范圍很廣，整個流場沒有激波的形成，流場參數緩慢過渡。

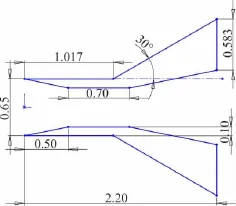
圖13 上下對稱尖劈示意圖Fig.13 Sketch map for symmetrical ramps

圖14 對稱尖劈流場密度等值線云圖Fig.14 Density contours for symmetrical ramps flow

4 結束語

在基于Boltzmann模型方程的氣體運動論統一算法中應用分區對接網格技術，實現了復雜流場中網格分區之間流場信息的正確傳遞，以及分區對接面上流場參數的光滑過渡，能夠實現對復雜外形的跨流域氣體流動問題數值模擬。研究表明，分區對接網格能夠實現對包括多體流場在內的復雜流動的正確描述，而且能夠更加準確地捕捉流場階躍、突變、過渡等特征。

［1］Wang Baoguo，Liu Shuyan.Calculation study of rarefied aerodynamics［M］.Beijing:Beihang University Press，2013.(in Chinese)王保國，劉淑艷.稀薄氣體動力學計算［M］.北京:北京航空航天大學出版社，2013.

［2］Boltzmann L.Weitere studien uber das warm egleichgewicht unter gas molekulen［J］.Sitzungs Berichte kaiserl.Akad.Der wissenschaften，1872，66(2):275-370.

［3］Gilberto Medeiros Kremer.An introduction to the Boltzmann equation and transport processes in gases［M］.Brazil:Interaction of Mechanics and Mathematics，2010.

［4］Chapmann S，Cowling T G.The mathematical theory of non-uniform gases［M］.London:Cambridge university Press，1990.

［5］Bhatnagar P L，Gross E P，Krook M.A model collision processes in gases［J］.Phys.Rev.，1954，94:511-525.

［6］Cheremisin F G.A two-level kinetic model for rotational-translational relaxations in a diatomic gas［J］.AIAA 2008-3932.

［7］James Maxwell Buick.Lattice Boltzmann methods in interfacial wave modelling［M］.Philosophy:The University of Edinburgh，1997.

［8］Xu Kun，Mao Meiliang，Tang Lei.A multidimensional gas-kinetic BGK scheme for hypersonic viscous flow［J］.Journal of Computational Physics，2005，203:405-421.

［9］Li Zhihui，Zhang Hanxin.Study on gas kinetic numerical algorithm using Boltzmann model equation［J］.Advances in Mechanics，2005，35(4):559-576.(in Chinese)李志輝，張涵信.基于Boltzmann模型方程的氣體運動論統一算法研究［J］.力學進展，2005，35(4):559-576.

［10］Li Zhihui，Zeng Shi.Simulation of planar couette flows using the gas-kinetic Boltzmann model［J］.J.of Tsinghua Univ.(Sci.＆Tech.)，2005，45(8):1103-1106.(in Chinese)李志輝，曾實.基于Boltzmann模型方程的平板Couette流計算［J］.清華大學學報(自然科學版)，2005，45(8):1103-1106.

［11］Li Zhihui，Zhang Hanxin.HPF parallel computation based on Boltzmann model equation for flows past complex body from various flow regimes［J］.Acta Aeronautica et Astronautica Sinica，2006，27 (2):175-181.(in Chinese)李志輝，張涵信.基于Boltzmann模型方程不同流區復雜三維繞流HPF并行計算［J］.航空學報，2006，27(2):175-181.

［12］Li Zhihui，Zhang Hanxin.Massive parallelization of gas-kinetic algorithm for Boltzmann model equation［J］.Chinase Journal of Computational Physics，2008，25(1):65-74.(in Chinese)李志輝，張涵信.求解Boltzmann模型方程的氣體運動論大規模并行算法［J］.計算物理，2008，25(1):65-74.

［13］Mao Meiliang，Deng Xiaogang，Xiang Daping.Applied study of method for multi-block patched mesh［J］.Acta Aerodynamica Sinica，2002，20(2):179-183.(in Chinese)毛枚良，鄧小剛，向大平.分區對接網格算法的應用研究［J］.空氣動力學學報，2002，20(2):179-183.

［14］Zhang Zhengke，Zhu Ziqiang，Zhuang Fenggan.Multiblock grid generation technique for multicomponent combination and its application［J］.Acta Aerodynamica Sinica，1998，16(3):311-317.(in Chinese)張正科，朱自強，莊逢甘.多部件組合體分塊網格生成技術及應用［J］.空氣動力學學報，1998，16(3):311-317.

［15］Rykov V A.Model kinetic equation of a gas with rotational degrees of freedom［J］.Fluid Dynamics，1975，10:959-966.

［16］Rykov V A，Titarev V A，Shakhov E M.Numerical study of the transverse supersonic flow of a diatomic rarefied gas past a plate［J］.Computational Mathematics and Mathematical Physics，2007，47(1):136-150.

［17］Wu Junlin，Li Zhihui，Jiang Xinyu.Study of one-dimensional shock-tube and two-dimension plate flows by solving Boltzmann-Rykov model equation involving rotational energy［J］.Chinese Journal of Computational Physics，2013，30(3):326-336.(in Chinese)吳俊林，李志輝，蔣新宇.考慮轉動能的一維/二維Boltzmann-Rykov模型方程數值算法［J］.計算物理，2013，30(3):326-336.

［18］Zhang Hanxin，Shen Mengyu.Computational fluid dynamics—fundamentals and applications of finite difference methods［M］.Beijing:National Defence Industry Press，2003.(in Chinese)張涵信，沈孟育.計算流體力學—差分方法的原理和應用［M］.北京:國防工業出版社，2003.

［19］Wu Junlin，Li Zhihui，Peng Aoping.Numerical simulation of unsteady flows from rarefied transition to continuum using the gas-kinetic unified algorithm［C］.Xi’an，Shaanxi:CSTAM 2013-A31-1100.(in Chinese)吳俊林，李志輝，彭傲平.氣體運動論統一算法對連續流到稀薄流非定常流場計算研究［C］.陜西西安:中國力學大會-2013論文集，2013，CSTAM2013-A31-1100.

［20］Li Z H，Zhang H X.Study on gas kinetic unified algorithm for flows from rarefied transition to continuum［J］.J.of Comput.Phys.，2004，193:708-738.

［21］Larina I N，Rykov V A.On boundary conditions for gases on a body surface［J］.Izv.Akad.Nauk SSSR，Mekh.Zhidk.Gaza，1986，5:141-148.

［22］Ketsdever A，Gnimelshein N.Radiometric phenomena:from the 19thto the 21stcentury［J］.Vacuum，2012，86:1644-1662.

Multi-block patched mesh in gas-kinetic unified algorithm

Wu Junlin，Peng Aoping，Li Zhihui*，Fang Ming
(Hypervelocity Aerodynamics Institute of China Aerodynamics Research and Development Center，Mianyang 621000，China)

In order to simulate gas flows with complex shapes or several bodies covering various regimes，coordinate space should be divided into dinky cells，and numerical method based on the complex mesh system should also be developed.In this paper，two-dimensional flows around complex objects are described by multi-block patched meshes，and then body-fitted mesh systems are given.Boltzmann-Rykov model equation involving rotational non-equilibrium effect is numerically computed based on this mesh system.Discrete velocity ordinate method is used to disperse velocity space，while finite-difference NND scheme for coordinate space.Transfer of distribution function on the interface，information and velocity information on the grid included，should be treated especially.Then flow characters from rarefied transition to continuum around complex bodies are obtained by numerical computing.Some examples show that macro-parameters glossily translate between different blocks in the whole mesh system.Results from GKUA are compared with those from reference and DSMC method.It is showed that the Gas-kinetic Unified Algorithm based on multi-block patched mesh is credible to numerically simulate complex flows in various regimes.

multi-block patched mesh;gas-kinetic unified algorithm;Rykov model equation;flow with several bodies

O355;O356

:Adoi:10.7638/kqdlxxb-2014.0016

0258-1825(2015)05-0624-07

2014-03-17;

:2014-05-22

國家自然科學基金(91016027，11325212);國家重點基礎研究發展計劃(2014CB744100)資助

吳俊林(1985-)，男，四川會理人，碩士，助理研究員，主要從事稀薄氣體動力學研究.E-mail:wujunlin130@aliyun.com

李志輝*，男，博士，研究員.Tel:13693524532，E-mail:zhli0097@x263.net

吳俊林，彭傲平，李志輝，等.分區對接網格在跨流域氣體運動論統一算法的應用研究［J］.空氣動力學學報，2015，33(5):624-630.

10.7638/kqdlxxb-2014.0016 Wu J L，Peng A P，Li Z H，et al.Multi-block patched mesh in gas-kinetic unified algorithm［J］.Acta Aerodynamica Sinica，2015，33(5):624-630.