旋轉鈍錐高超聲速自由飛氣動導數非對稱性

蔣增輝，宋 威，陳 農

（中國航天空氣動力技術研究院，北京 100074）

0 引 言

旋轉飛行器是在飛行過程中，繞其縱軸旋轉的一類飛行器，通常包括地空導彈、反坦克導彈等戰術導彈，炮彈、火箭彈，以及再入飛行器等［1］。旋轉飛行方式具有能夠克服或減小氣動非對稱或推力偏心等干擾因素的影響，以及可以簡化控制系統等優點，但旋轉也帶來了一些新的問題，使得飛行器的空氣動力性能和飛行性能發生變化［2－3］。

軸對稱飛行器的氣動導數通常采用軸對稱假設來描述，也即認為靜、動導數及Magnus力矩導數數值在各個方向上是相等的［4－6］。但Jaffe［7］在對超聲速下10°旋轉尖錐和60°旋轉鈍錐兩個平面的自由飛數據進行分析時，發現采用對稱假設無法獲得較為合理的擬合結果，觀測值與擬合曲線存在明顯的“相差”，對稱假設的合理性因而受到懷疑。Lusardi［8－9］對Jaffe的試驗數據進行了進一步的分析，發現只有靜導數符合軸對稱假設，而動導數和Magnus力矩導數均不符合軸對稱假設，并指出旋轉鈍錐在超聲速小迎角下氣動力的非對稱是由于邊界層位移厚度畸變造成的。Levy和Tobak［10］也認為旋轉錐的氣動阻尼存在非對稱的問題。上述研究僅對氣動導數的非對稱性的存在作了證明，沒有對各個氣動導數的非對稱程度進行深入分析，也沒有分析其對飛行器瞬態角運動和動穩定性預測的影響。

關于非對稱氣動導數對飛行器瞬態角運動影響的研究，未見到試驗分析的文獻發表。Hodapp［11］采用準靜態分析理論研究了不同的非對稱氣動導數對旋轉再入體瞬態角運動的影響。張魯民［12］通過六自由度彈道方程對再入彈頭非對稱靜、動導數對配平迎角的影響進行了數值模擬研究。

本文將在已開展的高超聲速下雙平面拍攝10°旋轉鈍錐風洞自由飛試驗［13］結果的基礎上，對旋轉鈍錐在高超聲速自由飛行狀態下氣動導數的非對稱性問題進行深入分析，并通過對氣動導數軸對稱假設下和考慮非對稱性的辨識結果進行比較，分析氣動導數的非對稱性對飛行器瞬態角運動和動穩定性預測的影響。

1 角運動方程

為便于對氣動導數軸對稱假設和考慮非對稱性的辨識結果進行比較，本文的數據分析方法采用直接對角運動方程中的參數進行辨識而獲得氣動導數的Chapman－Kirk方法［14］，而不采用較為簡易的三周期法。

考慮氣動導數非對稱性，旋轉速度為常值的飛行器其線性角運動模型為［8－9，15］：

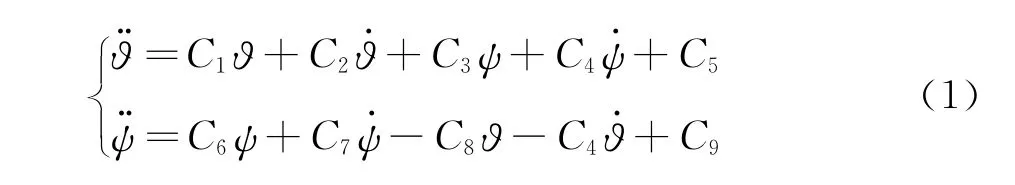
式中，C1＝CmαQsd／I，C2＝（Cmq＋）Qsd2／（2IV），C3＝ －pCmpβQsd2／（2IV），C4＝ －pIx／I，C6＝ －Cnβ·Qsd／I，C7＝ （Cnr－）Qsd2／（2IV），C8＝pCnpα·Qsd2／（2IV）。其中，I為模型的俯仰（偏航）轉動慣量，Cmα及Cnβ分別為模型俯仰、偏航靜導數系數，Cmq＋及Cnr－Cnβ·分別為俯仰、偏航動導數系數，Cmpβ及Cnpα分別為俯仰、偏航Magnus力矩導數系數，Ix為滾轉方向轉動慣量，p為滾轉速度，Q為動壓，s為參考面積，d為模型最大直徑，V為來流速度。其中角位移?為俯仰角，角位移ψ為偏航角。

初始條件為當t＝0時，?＝?0，＝，ψ＝ψ0＝。

在軸對稱假設下，Cmα＝ －Cnβ，Cmq＋Cmα·＝Cnr－Cnβ·，Cmpβ＝Cnpα，則角運動模型簡化為：

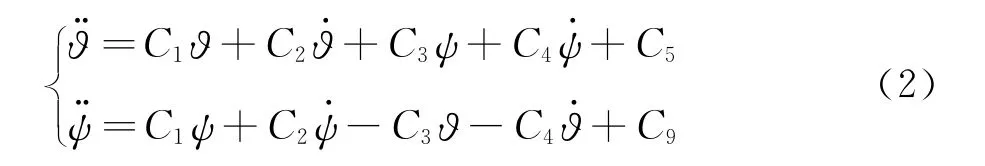
由方程組（1）或（2）出發，結合觀測值 ｛ti，?i，ψi｝i＝0，1，···，n，采用參數微分法進行參數辯識，可以識別出方程中的參數C1～C9，并進而通過式（1）或（2）獲得俯仰和偏航靜、動導數以及Magnus力矩導數。

2 辨識結果與分析

以在中國航天空氣動力技術研究院FD－07風洞中進行的10°半錐角旋轉鈍錐高超聲速（M＝6）雙平面拍攝風洞自由飛試驗結果作為觀測值（高速攝像機拍攝速率為2 000幀／秒）。試驗分兩組進行，均為軸對稱外形，除第二組模型尾部對稱布置了四條小片條外完全相同，如圖1所示。兩組模型的試驗條件也完全相同，發射時設計轉速約為1 200r／min。

根據在俯仰和偏航兩平面拍攝到兩組試驗模型飛行軌跡，分別由方程組（1）和（2）出發辨識得到在軸對稱假設下和考慮氣動導數非對稱性的辨識曲線如圖2～圖5所示，可以看到，雖然兩種情況下辨識曲線與觀測值均大體符合較好，但軸對稱假設下和考慮氣動導數非對稱性的辨識曲線存在一定區別，圖2～圖5顯示兩種模型在軸對稱假設下的辨識曲線與觀測值均存在一定的相位差，而考慮氣動導數非對稱性的辨識曲線則均不存在這一問題，與觀測值曲線重合較好。這說明軸對稱假設下獲得的辨識結果將存在一定偏差，而考慮氣動導數非對稱性的辨識結果較為合理可靠。

兩組試驗辨識結果及估計值的或然誤差分別如表1和表3所示，根據辨識結果換算得到的氣動導數分別如表2和表4所示。本文所采用的辨識方法其估計值或然誤差的表達式見文獻［16－18］。

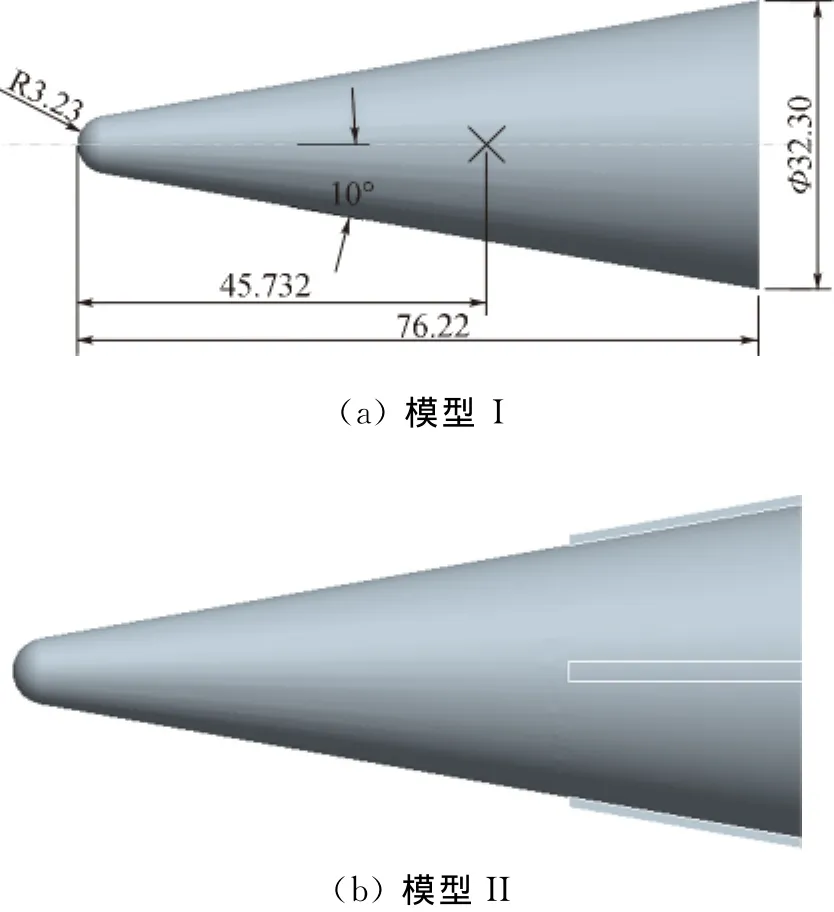
圖1 試驗模型外形圖Fig.1 Schematic of models

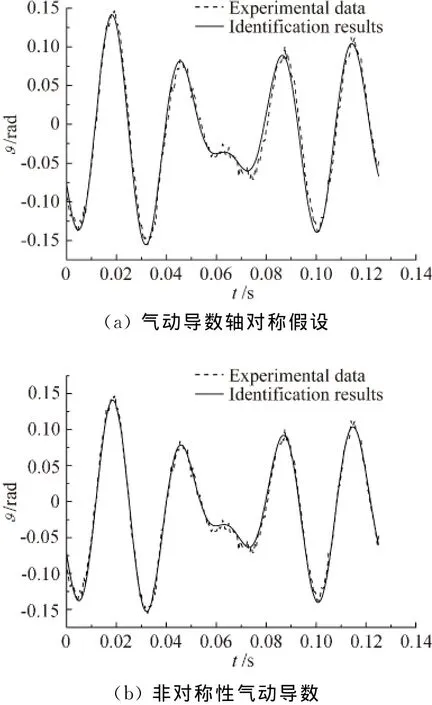
圖2 模型I俯仰平面氣動導數辨識曲線Fig.2 Identification curves of aerodynamic derivatives in pitch plane of model I

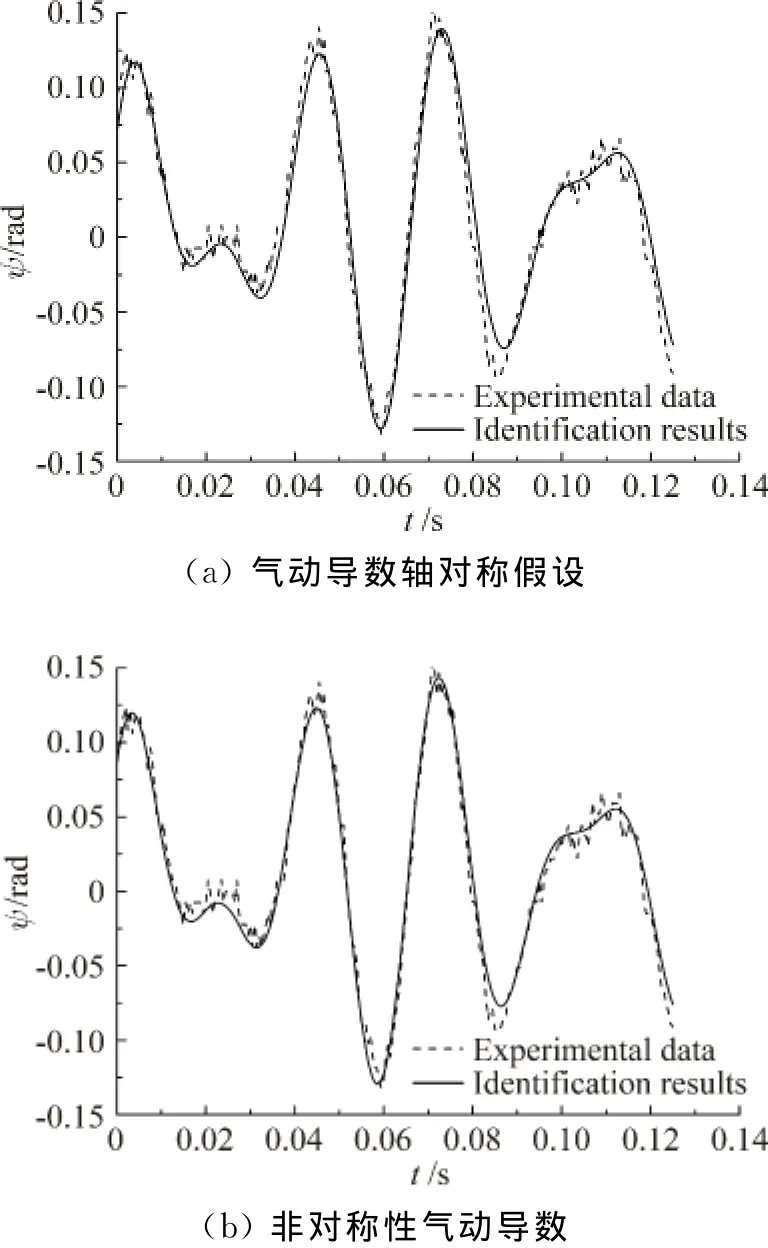
圖3 模型I偏航平面氣動導數辨識曲線Fig.3 Identification curves of aerodynamic derivatives in yaw plane of model I

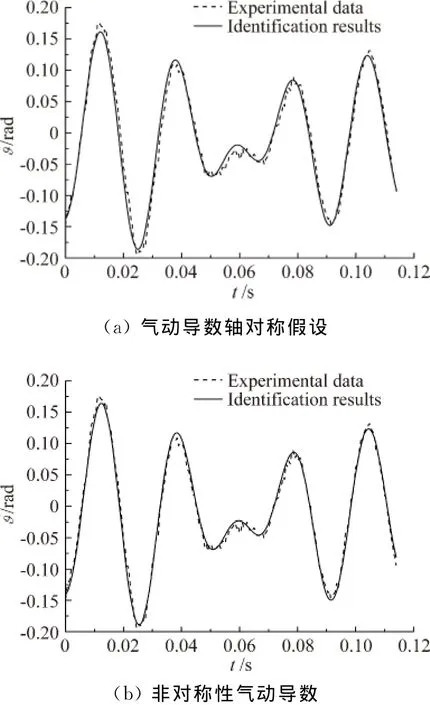
圖4 模型II俯仰平面氣動導數辨識曲線Fig.4 Identification curves of aerodynamic derivatives in pitch plane of model II

表1 模型I辨識結果Table 1 Parameters identified by model I

表2 模型I氣動力系數Table 2 Aerodynamic coeffcients of model I

表3 模型II辨識結果Table 3 Parameters identified by model II

表4 模型II氣動力系數Table 4 Aerodynamic coeffcients of model II

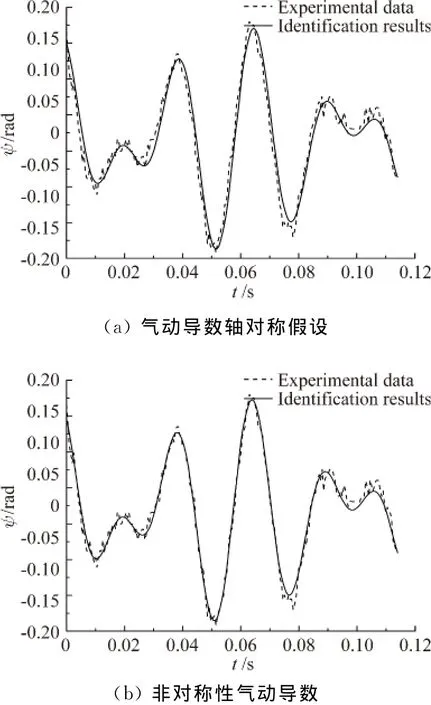
圖5 模型II偏航平面氣動導數辨識曲線Fig.5 Identification curves of aerodynamic derivatives in yaw plane of model II

Eikenbery在文獻［17］中指出該辨識方法的參數估計值及或然誤差都具有可靠的精度。可以看到，考慮非對稱性的辨識方程所得到的兩種模型靜導數的非對稱性均較小，兩個方向的系數幾乎相等，其比值Cmα／（－Cnβ）分別為1.009，和1／1.020，因此可近似認為其是對稱的；兩種模型在兩個方向的動導數系數則存在明顯的非對稱性，兩個方向數據差距較大；Magnus力矩導數系數在兩個方向上的差距也較為明顯。這說明在高超聲速下軸對稱旋轉飛行器也存在著文獻［8－9］在超聲速下獲得的氣動導數非對稱現象，且動導數的非對稱性最嚴重，Magnus力矩導數次之，而靜導數則幾乎不存在非對稱性。

對兩個方向的氣動導數系數取平均（見表2和表4），可發現兩組試驗的平均靜、動導數系數與采用軸對稱假設的結果較為相近，尤其是靜導數系數，幾乎相等；而Magnus力矩導數系數平均值則與軸對稱假設結果相差較大。這說明軸對稱假設下所得到的靜導數和動導數辨識結果可近似認為是兩個方向上的非對稱靜、動導數系數的平均值，且對靜導數預測結果基本沒有影響。但由于動導數存在明顯的非對稱，兩個方向動導數系數數值相差可達數倍，因此采用軸對稱假設得到的動導數系數（也即兩個方向近似平均值）雖然對于飛行器的動穩定性沒有根本性的預測偏差，但卻會對其中一個方向的動穩定性產生過于樂觀的預測，而對另一個方向的動穩定性預測則過低。由于軸對稱旋轉飛行器俯仰和偏航方向的動導數差別較大，因此只對其一個方向的動導數進行測量來評估其動穩定性是不充分的，另一方向的動導數也應當測量。

此外，表2和表4均表明，在軸對稱假設下由試驗觀測值反算得出的轉速也比考慮非對稱因素反算而得的數值要偏大。

3 氣動導數非對稱性影響分析

圖6和圖7分別為兩組試驗在軸對稱假設下和考慮非對稱性辨識得到的?－ψ圖。可以看到，考慮氣動導數非對稱性的?－ψ圖與觀測值的重合度均明顯較軸對稱假設下要好，說明前者獲得的瞬態角運動?－ψ圖更符合實際情況。兩種辨識結果的?－ψ圖差異明顯，因此氣動導數的非對稱性對瞬態角運動存在明顯影響，采用軸對稱假設獲得的瞬態角運動將存在一定誤差。由于靜導數幾乎不存在非對稱問題，而動導數非對稱性較為嚴重，因而旋轉鈍錐?－ψ圖在對稱假設和考慮非對稱導數兩種情況下的差異主要是由動導數的差異引起，且與Hodapp［11］采用理論分析的方法得到的完全由靜導數非對稱引起的?－ψ圖相比，其差異明顯要小，這說明由動導數非對稱占主導的情況下對瞬態角運動的影響要比靜導數非對稱的影響要小。

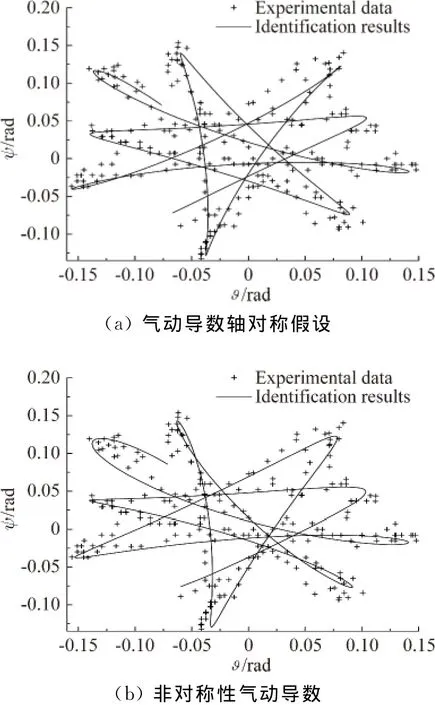
圖6 模型I?－ψ圖Fig.6 ?－ψplots of model I

圖7 模型II?－ψ圖Fig.7 ?－ψplots of model II

圖8和圖9則分別為兩種模型總迎角－時間曲線辨識結果（總迎角Θ＝β分別為迎角和側滑角）。與?－ψ圖類似，考慮非對稱性的總迎角曲線與觀測值的重合度明顯較軸對稱假設下要好。兩組試驗辨識結果均顯示，在軸對稱假設下辨識得到的總迎角峰、谷值中有較多明顯與相應的觀測值峰、谷值不重合，相位與觀測值也多有差異；而考慮非對稱性的辨識結果無論峰、谷值與相位均與觀測值符合較好，這說明氣動導數的非對稱性對總攻角值也有明顯影響。因此采用軸對稱假設獲得的總迎角也存在誤差。同樣可以發現，本文中由動導數非對稱占主導的情況下對總迎角的影響比文獻［11］中完全由靜導數非對稱造成的影響要小。

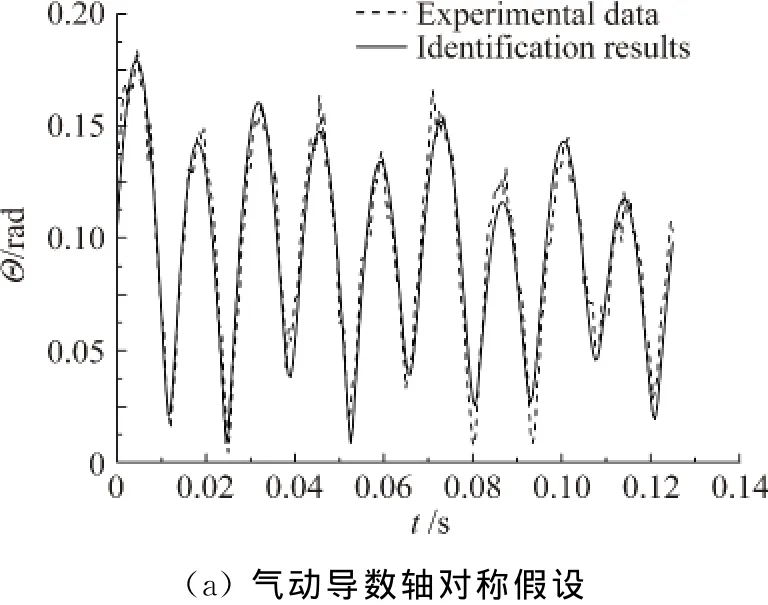
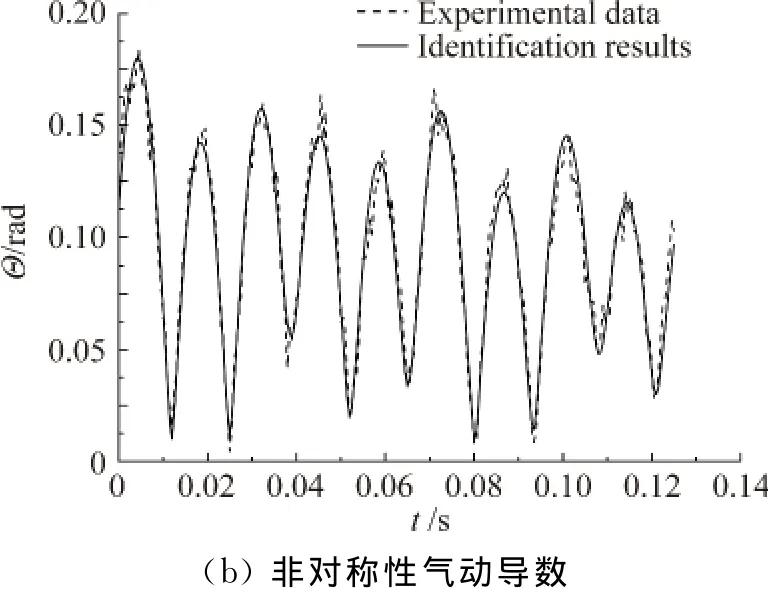
圖8 模型I總迎角－時間曲線Fig.8 Curves of total angle of attack vs.time of model I

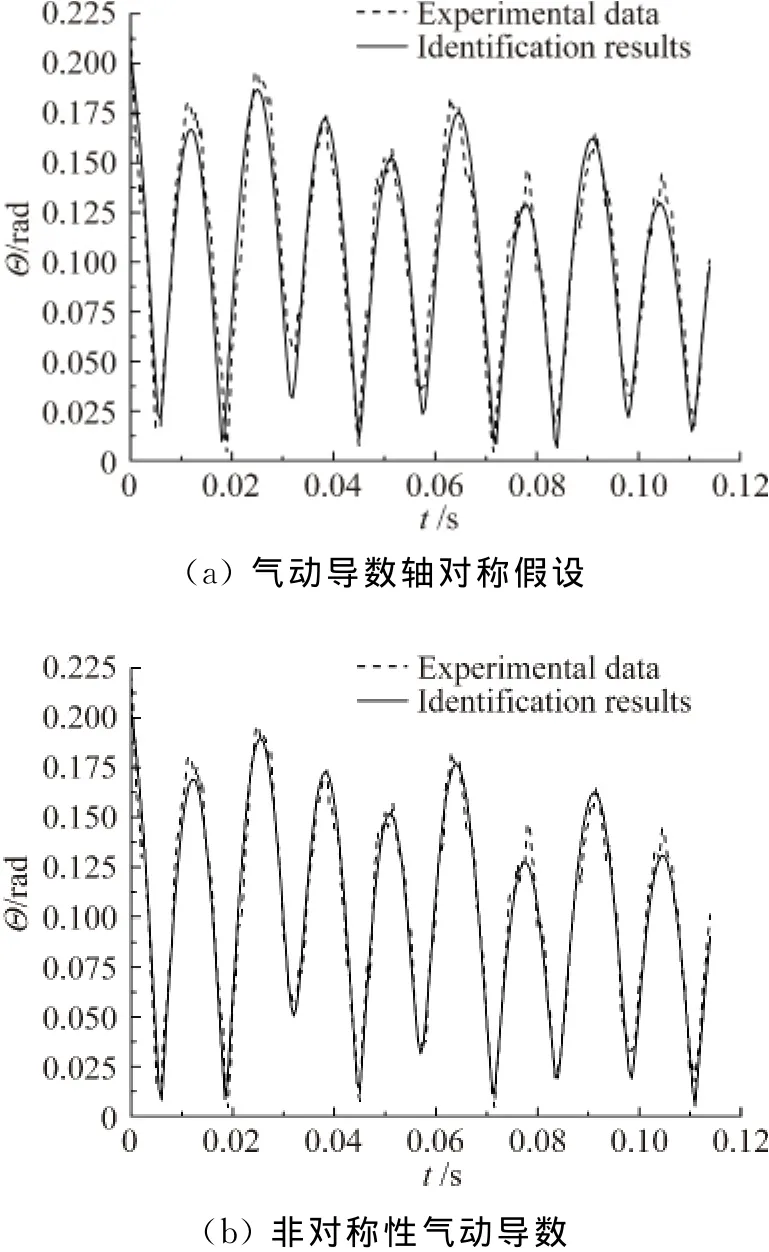
圖9 模型II總迎角－時間曲線Fig.9 Curves of total angle of attack vs.time of model II

4 結 論

通過分別采用氣動導數軸對稱假設和考慮非對稱性的角運動方程，對雙平面拍攝10°旋轉鈍錐高超聲速風洞自由飛試驗結果的辨識結果進行比較，證明了高超聲速下軸對稱旋轉飛行器存在氣動導數（靜導數除外）的非對稱性，其中動導數的非對稱性尤其嚴重。采用軸對稱假設將無法獲得氣動導數的準確數值，而考慮氣動導數非對稱性的辨識結果則更加接近真實值。氣動導數的非對稱性對瞬態角運動以及總迎角的峰、谷值及相位均存在明顯影響，因此其影響不可忽略。軸對稱假設獲得的瞬態角運動及總迎角都存在一定誤差，會對瞬態角運動及總迎角的準確預測產生影響。

［1］Gao Qingfeng，Liu Li，Chen Luojing.Criteria for the nonlinear dynamic stability of rotative vehicles［J］.Modern Defence Technology，2006，34（1）：19－23.（in Chinese）高慶豐，劉莉，陳羅婧.旋轉飛行器非線性運動穩定性判據［J］.現代防御技術，2006，34（1）：19－23.

［2］Miao Ruisheng，Wu Jiasheng.Aerodynamics of spinning projectiles［J］.Advances in Mechanics，1987，17（4）：479－488.（in Chinese）苗瑞生，吳甲生.旋轉彈空氣動力學［J］.力學進展，1987，17（4）：479－488.

［3］Xu Kefa，Wang Lingzhi，Li Mingjuan，et al.Research on dynamic derivative of spinning missile by six－degree－of－freedom free－flight test in wind tunnel［J］.Acta Aerodynamica Sinica，1993，11（3）：257－262.（in Chinese）許可法，王陵志，李明娟，等.旋轉導彈風洞六自由度自由飛動導數實驗研究［J］.空氣動力學學報，1993，11（3）：257－262.

［4］Qian Xingfang，Lin Ruixiong，Zhao Yanan.Missile flight dynamics［M］.Beijing Institute of Technology Press，2012：248－263.（in Chinese）錢杏芳，林瑞雄，趙亞男.導彈飛行力學［M］.北京理工大學出版社，2012：248－263.

［5］Yu Jianqiao，Wen Zhonghui，Mei Yuesong，et al.Tactical missile system design［M］.Beijing：Beijing University of Aeronautics ＆ Astronautics Press，2010：141－166.（in Chinese）于劍橋，文仲輝，梅躍松，等.戰術導彈總體設計［M］.北京航空航天大學出版社，2010：141－166.

［6］Chapman G T，Kirk D B.A new method for extracting aerodynamic coefficients from free－flight data［J］.AIAA Journal，1970，8（4）：753－758.

［7］Jaffe P.Nonplanar tests using the wind－tunnel free－flight technique［J］.J.Spacecraft，1973，10（7）：435－442.

［8］Lusardi R J，Nicolaides J D.The determination of non－symmetric aerodynamics of re－entry missiles［C］.AIAA－74－108，1974.

［9］Lusardi R J，Nicolaides J D.Determination of nonsymmetric aerodynamics of re－entry missiles［J］.J.spacecraft，1975，12（4）：193－198.

［10］Levy L L，Tobak M.Nonlinear aerodynamics of bodies of revolution in free flight［J］.AIAA Journal，1970，8（12）：2168－2171.

［11］Hodapp A E Jr.Effects of unsymmetrical stability derivative characteristics on re－entry vehicle transient angular motion［J］.J.Spacecraft，1975，13（4）：82－90.

［12］Zhang Lumin.Research on unsymmetrical aerodynamics of reentry warhead［J］.Journal of Astronautics，1989，（4）：45－50.（in Chinese）張魯民.再入彈頭非對稱氣動力研究［J］.宇航學報，1989，（4）：45－50.

［13］Jiang Zenghui，Chen Nong.Wind tunnel free－flight test with biplanar optical system on the spinning blunt cone［J］.Chinese Journal of Theoretical and Applied Mechanics，2013，45（5）：777－781.（in Chinese）蔣增輝，陳農.旋轉鈍錐雙平面拍攝風洞自由飛試驗［J］.力學學報，2013，45（5）：777－781.

［14］Ma Jiahuan，Tang Zongheng，Zhang Xiaoping.Free flight method in hypersonic impulse type tunnels for static and dynamic stability study［J］.Acta Aerodynamica Sinica，1983，（4）：77－85.（in Chinese）馬家驩，唐宗衡，張小平.在高超聲速脈沖型風洞中測量靜、動穩定性導數的模型自由飛方法［J］.空氣動力學學報，1983，（4）：77－85.

［15］Ingram C W，Lusardi R J.Effects of rifling and n－vanes on the Magnus characteristics of bodies of revolution［R］.AIAA－72－970，1972.

［16］Han Zipeng，et al.Exterior ballistics of projectiles and rockets［M］.Beijing：Beijing Institute of Technology Press，2008：23－25.（in Chinese）韓子鵬，等.彈箭外彈道學［M］.北京理工大學出版社，2008：23－25.

［17］Eikenbery R S.Analysis of the angular motion of missiles［R］.SC－CR－70－6051，1970.

［18］Ma Jiahuan，Tang Zongheng，Zhang Xiaoping，et al.The measurements of the static and dynamic stability derivatives of conical models in the shock tunnel［J］.Chinese Journal of Theoretical and Applied Mechanics，1980，（1）：84－89.（in Chinese）馬家驩，唐宗衡，張小平，等.激波管風洞中錐模型靜、動穩定性導數的測量［J］.力學學報，1980，（1）：84－89.

［19］Trickey C M，Edwards J A，Shaw S.Experimental and computational assessment of the dynamic stability of a supersonic square missile［C］.AIAA 2004－5454，2004.

［20］Gkritzapis D N.Computational atmospheric trajectory simulation analysis of spin－stabilized projectiles and small bullets［R］.AIAA 2007－6584.