基于車體剛體與彈性合成的重型汽車平順性分析

李 杰， 王文竹， 趙 旗

(吉林大學 汽車仿真與控制國家重點實驗室，長春 130025)

基于車體剛體與彈性合成的重型汽車平順性分析

李 杰， 王文竹， 趙 旗

(吉林大學 汽車仿真與控制國家重點實驗室，長春 130025)

為了研究重型汽車的平順性問題，運用兩端自由等截面彈性梁理論，建立了車體剛體與彈性合成的4自由度1/2重型汽車振動模型。應用頻域分析方法推導了基于前輪的系統頻率響應特性和響應量的頻率響應特性，確定了響應量的功率譜密度和均方根值。基于車體剛體與彈性合成模型和剛性模型，采用Matlab開發了相應的重型汽車平順性仿真程序。通過與剛體模型的平順性仿真結果對比表明：車體的彈性對重型汽車的平順性影響很大，在重型汽車的平順性研究中不能忽略。

車輛工程；重型汽車；平順性；彈性梁

重型汽車因為高效、成本低和低油耗，成為公路的主要運輸工具[1]。重型汽車經常處于長途高速運貨狀態，駕駛員容易疲勞引發交通事故，貨物容易損壞。因此，其平順性的研究至關重要。

以往重型汽車平順性的研究，往往將車架假設成剛體[2]。然而，重型汽車具有車長、軸距大、承載重和車體彈性表現十分明顯等特點，所以，進行重型汽車平順性分析，無法忽略車體的彈性[3]。本文以兩端自由等截面彈性梁理論為基礎，建立基于車體剛體與彈性合成的4自由度振動模型，應用頻域分析方法進行理論分析與仿真，并與車體剛體模型的平順性仿真結果進行比較，以說明車體彈性對重型汽車平順性的影響。

1 振動模型的建立

1.1 兩端自由等截面彈性梁的彎曲振動

假設車體即懸載質量為等截面彈性梁，且兩端自由，則等截面彈性梁的彎曲振動方程為[4]

(1)

式中：z(x,t)為彎曲振動位移；EI為彎曲剛度；ρ為單位長度質量；f(x,t)為作用在梁上的分布載荷。

當兩端自由等截面彈性梁自由振動時，f(x,t)=0。將z(x,t)在時間和空間上分離[5]，則

z(x,t)=φ(x)qe(t)

(2)

式中：φ(x)為彈性梁振型函數；qe(t)為廣義坐標。

將式(2)代入式(1)，可得兩端自由等截面彈性梁的振型函數為

(3)

1.2 兩端自由等截面梁剛體與彎曲振動的運動合成

假設兩端自由等截面彈性梁在平面內既做剛體運動，又做彎曲振動。以彈性梁前端建立慣性坐標系，如圖1所示。

運動合成后，梁上任一點的垂直位移可以表示為

zre(x)=zc+(x-xc)θ+ze

(4)

式中：zre為梁上任一點的垂直位移；ze為彈性梁彎曲振動引起的垂直位移。

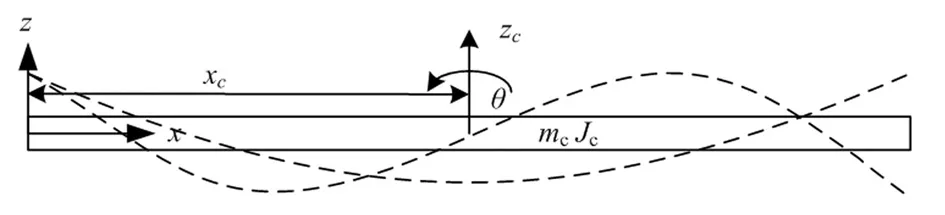
圖1 兩端自由等截面彈性梁運動合成Fig.1 Motion synthesis of elastic beam of equal section with both free ends

由模態疊加原理，彈性梁彎曲振動引起的垂直位移ze可由前n個振型函數的線性組合表示[6]，即

(5)

由于在所有振型函數中，低級振型函數占主導作用[4-5]，因此，將n取2，則梁上任一點的垂直位移就可以表示為

zre=zc+(x-xc)θ+φ1(x)ze1+φ2(x)ze2

(6)

1.3 重型汽車振動系統力學模型

假設汽車左右質量對稱分布，左、右車輪的路面激勵相同，將車體看成均質的彈性梁來建立重型汽車的1/2汽車振動模型，如圖2所示。圖中，zc和θ分別為車體質心的剛體垂直位移和剛體縱向角位移，qf和qr分別為前輪和后車輪處路面激勵，mc和Jc分別為車體和車體繞其質心的縱向轉動慣量，cf和cr分別為前懸架和后懸架的垂直阻尼，kf和kr分別為前懸架和后懸架的垂直剛度，xc、xf和xr分別為車體質心、前軸和后軸至彈性梁前端的距離。

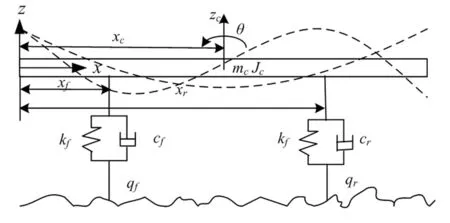
圖2 4自由度1/2重型汽車振動模型Fig.2 Vibration model of 4 DOF half heavy-duty automobile

振動模型的自由度，為車體質心的垂直位移、俯仰角位移和車體的前二階彈性彎曲振動位移，共4個自由度。

1.4 振動系統的能量

振動系統的動能為

(7)

(8)

式中：me1為車體一階模態質量；me2為車體二階模態質量。

振動系統的勢能為

(9)

(10)

式中：ke1為車體一階模態剛度；ke2為車體二階模態剛度。

振動系統的耗散能為

(11)

1.5 重型汽車振動系統數學模型

由圖1所示的振動力學模型，根據拉格朗日方程，由振動系統能量得到數學模型為

(12)

{z}={zc,θ,ze1,ze2}T，{q}={qf,qr}T

(13)

[m]=diag(mc,Jc,me1,me2)

(14)

(15)

(16)

(17)

(18)

(19)

式中：p=c,k；ce1=ce2=0。

2 頻域分析

2.1 基于前輪的系統頻率響應特性

對式(12)兩邊進行傅里葉變換，可得到頻率響應函數為

(-ω2[m]+jω[m]+[k])-1([kq]+jω[cq])

(20)

式中：j為虛數單位；{z(ω)}為{z}的傅里葉變換；{q(ω)}為{q}的傅里葉變換。

假設汽車前后輪統計特性相同，軌跡相同，則前后輪輸入的時間路面功率譜密度的關系為[7]

(21)

式中：qr(ω)為qr的傅里葉變換；qf(ω)為qf的傅里葉變換；u為車速。

于是，路面激勵向量的傅里葉變換為

(22)

式中：{Hq(ω)}為以前輪為輸入、路面激勵向量為輸出的頻率響應特性。

由式(20)和式(22)，可得基于前輪輸入的系統頻率響應特性函數為

(23)

2.2 響應量的頻率響應特性

為了說明車體彈性對重型汽車平順性的影響，以車體質心處垂直加速度、車體前懸架處垂直加速度和車體后懸架處垂直加速度作為響應量。

由式(6)，可得車體任意一點加速度為

(24)

由此可得基于前輪輸入的車體任意一點加速度頻率響應特性函數為

(25)

在式(25)中分別代入x=xc,xf,xr，就可分別得到車體質心處垂直加速度、車體前懸架處垂直加速度和車體后懸架處垂直加速度的頻率響應特性。

2.3 響應量的功率譜密度和均方根值

根據隨機振動理論，響應量的功率譜密度為[8]

(26)

(27)

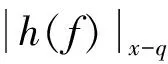
由響應量的功率譜密度，可得振動應量的均方根值為

(28)

式中：fl為頻率下限；fu為頻率上限。

3 整車平順性仿真程序的開發與實例仿真

進行汽車平順性仿真，基于車體剛體與彈性合成模型和傳統的車體剛性模型[8]，使用Matlab開發了相應的仿真程序，程序流程，如圖3所示。

所開發的仿真程序，由參數輸入模塊、車體剛體與彈性合成模型系統矩陣模塊、車體剛性模型系統矩陣模塊、振動響應量對前輪處路面激勵的頻率響應函數模塊、前輪路面激勵功率譜密度確定模塊、振動響應量功率譜密度和均方根值模塊、計算結果顯示與輸出模塊等組成。其中，車體剛體與彈性合成模型系統矩陣模塊，又包含連接點彈性位移、模態質量和模態剛度、合成模型系統矩陣子模塊。

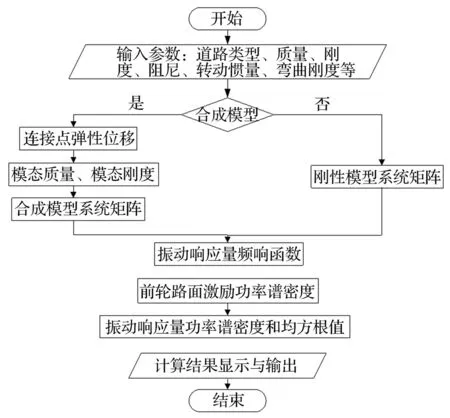
圖3 程序流程圖Fig.3 Program flow chart

以某重型車為計算對象[2]，仿真工況為汽車以50 km/h的速度在C級路面上行駛。仿真結果，如表1、圖4和圖5所示。圖4和圖5中，剛彈模型，是基于車體剛體和彈性合成模型的簡稱；剛體模型，是基于車體剛性而不考慮其彈性的傳統模型。

表1 垂直加速度均方根值的比較

由圖4可以看出，剛彈模型的車體質心垂直加速度功率密度比剛體模型多了一個峰值，發生在車體第一階固有頻率處，而二階固有頻率處沒有出現峰值，這是因為質心位置是第二階振型的節點；剛彈模型在車體前后懸架處垂直加速度功率密度比剛體模型多出了兩個峰值，分別在車體的兩階固有頻率處出現。

由圖5可以看出，振動響應量的均方根值的變化趨勢與功率譜密度曲線相似。

圖4 響應量的功率譜密度Fig.4 Power spectral density of response variables

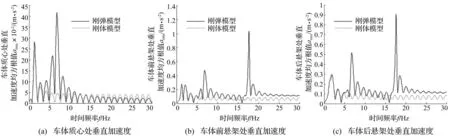
圖5 響應量的均方根值Fig.5 RMS value of response variables

由表1可以看出，剛彈模型和剛體模型的車體加速度均方根值相差較大，其中前懸架處加速度均方根值的差異最大，達到了110%。

通過兩種模型仿真結果對比，可以看出車體的彈性對重型汽車平順性產生了很大的影響，要對重型汽車的平順性進行正確評價，必須考慮車體的彈性。

4 結 論

以1/2重型汽車為研究對象，將車體看成兩端自由等截面彈性梁，對考慮車體剛體與彈性合成的4自由度汽車振動系統進行了力學描述，應用拉格朗日方程推導出矩陣形式的系統振動數學模型。應用頻域分析方法，推導了基于前輪的系統頻率響應函數和振動響應量頻率響應函數，由此可以確定振動響應量的功率譜密度和均方根值。

通過基于車體剛體與彈性合成模型和剛體模型平順性仿真結果的對比可以看出，車體的彈性對重型汽車平順性產生很大影響，在進行重型汽車平順性分析時必須考慮車體的彈性。

[1] 秦玉英．汽車行駛平順性建模與仿真的新方法研究及應用[D]．長春：吉林大學汽車工程學院，2009.

[2] Cole D J，Cebon D．Spatial repeatability of dynamic tyre force generated by heavy vehicles[J]．Proceedings of the Institution of Mechanical Engineers，Part D，Journal of Automobile Engineering，1993，206(3)：17-27．

[3] 楊波，王學林，胡于進,等．基于柔性模型的多軸汽車平順性的研究仿真[J]．汽車工程，2003，25(5)：481-486． YAN Bo，WANG Xue-lin, HU Yu-jin, et al．A simulation study on ride comfort of multi-axle vehicle base on flexible model[J]．Journal of Automotive Engineering，2003，25(5)：481-486．

[4] 劉延柱，陳文良，陳立群．振動力學[M]．北京：高等教育出版社，1998．

[5] 陳宇東．結構振動分析[M]．長春：吉林大學出版社，2007．

[6] IBRAHIM I M．A generally applicable 3d truck ride simulation with coupled rigid bodies and finite element models[J]．Int. J. of Vehicle Design， 2004，11(1)：67-85．

[7] 車華軍．遺傳算法在汽車行駛平順性仿真研究中的應用[D]．長春：吉林大學汽車工程學院，2004．

[8] 余志生．汽車理論[M]．北京：機械工業出版社，2000．

Ride comfort analysis of heavy-duty automobile based on a rigid-elastic synthesis model of vehicle body

LI Jie, WANG Wen-zhu, ZHAO Qi

(State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China)

In order to study the ride comfort of heavy-duty automobile, a 4 DOF vibration model of the half heavy-duty automobile based on the rigid-elastic synthesis of vehicle body was established by using the elastic theory of beams of equal cross sections with both free ends. Frequency response characteristics of the system and response variables based on the front wheel part were derived by the analysis method in frequency domain. The power spectral density and the root mean square value of response variables were determined. The corresponding simulation programs for the ride comfort of heavy-duty automobile were developed based on the rigid-elastic synthesis model and the rigid model of vehicle body with Matlab. By comparing the simulation results of both models, it is shown that vehicle body flexibility has a great impact on ride comfort of heavy-duty automobile and it cannot be ignored in ride comfort dosign of heavy-duty automobile.

vehicle engineering; heavy-duty automobile; ride comfort; elastic beam

國家“863”高科技資助項目(2006AA110104)

2014-01-26 修改稿收到日期：2014-05-06

李杰 男，教授，博士生導師，1964年生

U461.4

A

10.13465/j.cnki.jvs.2015.09.011