溫度影響下FGM圓環板的面內自由振動分析

滕兆春, 蒲 育

(蘭州理工大學 理學院，蘭州 730050)

溫度影響下FGM圓環板的面內自由振動分析

滕兆春, 蒲 育

(蘭州理工大學 理學院，蘭州 730050)

基于二維彈性理論和Hamilton原理，假設材料物理性質隨溫度變化且沿圓環板徑向按照冪律梯度分布，導出了溫度影響下FGM薄圓環板面內自由振動的運動微分方程。用微分求積法(DQM)計算了溫度影響下FGM圓環板面內自由振動的無量綱頻率，并與各向同性材料圓環板面內自由振動的無量綱頻率進行了比較，說明該分析方法的有效性。同時考慮了沿圓環板徑向均勻升溫和非均勻升溫兩種情況下，幾何參數、材料性質和溫度變化對面內自由振動頻率的影響。

FGM圓環板；初始熱應力；面內自由振動；無量綱頻率；Hamilton原理；微分求積法

圓(環)板的面內自由振動，在工程領域中有十分重要的意義和廣泛的應用背景。例如轉動圓(環)板的轉動噪音消除以及面內振動頻率在壓電圓片設計中的參考價值。此外，圓(環)板面內振動研究在工程中的車輪、盤式剎車片以及驅動器硬盤等結構元件中也具有潛在的應用。近些年，隨著新材料的興起，功能梯度材料作為一種新型復合材料，越來越多受到人們的關注。由于功能梯度材料在高的溫度梯度環境下能減小熱變形及緩解熱應力，故功能梯度材料圓(環)板在核工業、船舶，航空航天和化學工業等領域受到廣泛的應用，從而研究功能梯度材料圓(環)板的振動問題顯得尤為重要。許多學者從不同的角度大量研究了各向同性材料圓(環)板的橫向振動[1]，然而圓(環)板面內自由振動的研究相對較少[2-4]。文獻[5]研究了厚板的面內振動，而文獻[6]得出了夾支圓板面內自由振動固有頻率方程的解析解。文獻[7]研究了圓(環)板在四種經典邊界條件下的面內自由振動，應用邊界正交多項式特性和Rayleigh-Ritz法得出了固有頻率和相應的振型。文獻[8]研究了圓環板在內、外部彈性支承約束條件下的面內自由振動，得出增加固支支承點會引起不同高階振型分化成兩個不同的頻率。文獻[9]用Ritz法研究了均勻厚度超橢圓板的面內自由振動，引入Lagrange乘子以滿足邊界條件，并且得到了自由邊界條件和點支承邊界條件下橢圓板和矩形板等不同形狀板的面內自由振動的無量綱頻率。文獻[10-11]基于von-Karman板理論，研究了熱機載荷作用下，功能梯度圓板的非線性彎曲和過屈曲行為。文獻[12]基于三維線彈性理論，用半解析法研究了FGM圓板物性參數沿厚度方向變化的自由振動和強迫振動。然而溫度影響下FGM圓(環)板面內自由振動的研究目前在國內外還沒有相關的文獻報道。

這里研究了溫度影響下FGM薄圓環板的面內自由振動問題。假設材料物性隨溫度變化，且材料組分沿圓環板徑向按冪律梯度分布，首先基于二維熱彈性理論，得到初始熱應力，然后應用Hamilton原理和二維彈性理論推導出溫度影響下FGM薄圓環板面內自由振動的控制微分方程。采用微分求積法非均勻節點將控制微分方程沿圓環板徑向離散，同時也將相應的邊界條件離散，將微分方程組轉化為自由振動的特征值問題，從而求得面內自由振動的頻率，并與已有的各向同性材料圓環板面內自由振動的無量綱頻率進行了比較，證實所得的結果有效。最后研究了沿徑向均勻升溫和非均勻升溫兩種情況下，幾何參數、材料性質和溫度變化對頻率的影響。

1 控制微分方程及參數的無量綱化

1.1 溫度影響下功能梯度材料的物性關系

考慮厚度為h的FGM薄圓環板，設物性參數隨溫度變化，材料組分的體積分數沿徑向按冪律梯度分布，且溫度也沿徑向分布，其彈性模量為E，密度為ρ，泊松比為μ，外半徑為Ro，內半徑為Ri，徑向位移分量為u，周向位移分量為v，圓環板內部(r=Ri)為金屬材料，外部(r=Ro)為陶瓷材料，功能梯度材料圓環板的物性參數P(彈性模量E，泊松比μ，密度ρ，熱膨脹系數α，熱傳導率K)與徑向坐標r和溫度T滿足

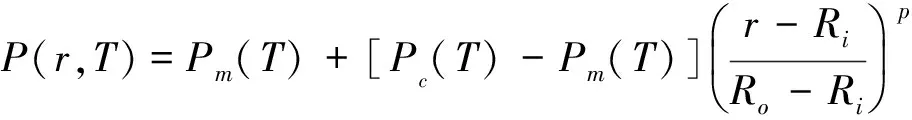
式中：p為梯度指標，下標m與c分別為金屬和陶瓷。陶瓷和金屬兩種材料的某一物性參數G隨溫度T變化的函數關系為[13-14]：

G(T)=G0(1+G1T+G2T2)

(2)

式中：Gi(i=0,1,2)為材料系數。

1.2 初始熱應力的計算

假設FGM薄圓環板內無熱源，溫度沿圓環板徑向方向分布，由一維熱傳導方程

(3)

考察邊界條件：r=Ri時，T=Tm

r=R0時，T=Tc

(4)

式(3)在邊界條件式(4)下的解可由多項式表示為

(5)

式中:

當溫度變化時，FGM圓環板內的初始熱應力[14-15]

(6)

式中：σ0r,σ0θ,τ0rθ為初始熱應力，ΔT=T-T0，T0為無應力狀態時的溫度。

(7)

1.3 自由振動分析

當圓環板達到熱平衡狀態后受外界一擾動(激勵)，此時圓環板內任一點將在熱平衡位置自由振動，設達到熱平衡狀態相對于未變形狀態任意一點的初始位移分別為u0(r,θ)，v0(r,θ)，由于自由振動所產生的位移分別為u(r,θ,t)，v(r,θ,t)，則任意一點的總位移分別為：

由于考慮板內初始熱應力的影響，應變滿足

(8)

式中：上標L表示線性項應變，NL表示非線性項應變。線性項應變與位移之間的關系為

(9)

非線性項應變與位移之間的關系為

(10)

由二維彈性體本構關系

(11)

對圓環板應用Hamilton原理

(12)

(13)

圓環板彈性勢能的變分為

(14)

當達到熱平衡狀態后，初始應變的變分δε0r=δε0θ=δγ0rθ=0，且τ0rθ=0。本文只考慮線性自由振動，故略去式(14)中乘積項的非線性高階無窮小量，從而式(14)可簡化為

(15)

將式(9)～式(11)，式(13)和式(15)代入式(12)，由變分原理及分部積分法可得溫度影響下功能梯度材料薄圓環板面內自由振動的運動微分方程和相應的邊界條件分別如下：

(16)

(17)

邊界條件為

u=v=0

(18)

或

(19)

(20)

式中：n為環向波數，t為時間，i為虛數單位，ω為固有頻率。將式(20)代入式(16)和式(17)，且無量綱化如下：

(21)

(22)

(23)

2 DQM離散及特征值問題

式(22)和式(23)系數中包含初始熱應力項，且微分方程為變系數常微分方程組。許多實例已證實DQM作為求解變系數微分方程(組)的有效方法，具有離散節點個數較少、計算精度高、易收斂、工作量小等優點。采用DQM且參考文獻[16]，FGM圓環板在徑向方向的節點劃分采用如下的公式：

(24)

其中N為節點總數。式(22)和式(23)用DQM分別離散后化為：

(25)

(26)

式中:Aij和Bij分別為一階導數和二階導數的權系數，且i=2,3,…,N-1，

考慮如下的兩種基本邊界條件：

(1) 夾緊 (C)

Un=Vn=0, 在x=β或1

(27)

(2) 自由 (F)

(28)

用DQM分別離散邊界條件式(27)和式(28)得

Uni=Vni=0，i=1或N

(29)

(30)

將式(29)和式(30)對應組合后可得不同類型離散化后的邊界條件：

內部夾緊-外部夾緊(C-C)

內部自由-外部自由(F-F)

內部自由-外部夾緊(F-C)

內部夾緊-外部自由(C-F)

控制式(25)～式(26)與邊界條件式(29)～式(30)對應聯立后便構成了不同邊界條件下面內自由振動的邊值問題。該邊值問題可用分塊矩陣形式表示為：

(31)

{wb}=[Un2,Un3,…,Un(N-1),Vn2,Vn3,…,Vn(N-1)]T
{wd}=[Un1,UnN,Vn1,VnN]T

式中:{wb}為圓環板內部的節點位移，{wd}為圓環板邊界處的節點位移。[Sbb]和[Sbd]是由運動方程導出的剛度矩陣，而[Sdb]和[Sdd]是由邊界條件導出的剛度矩陣。由式(31)消去{wd}，得自由振動的特征值問題

[S]{wb}-Ω2[I]{wb}={0}

(32)

式中:[S]=[Sbb]-[Sbd] [Sdd]-1[Sdb]，[I]為(2N-4)階單位陣，特征向量{wb}描述了溫度影響下FGM圓環板面內自由振動的振型。

3 計算結果與分析

計算中選取金屬材料為Ti-6Al-4V，陶瓷材料為ZrO2，它們隨溫度變化的物性系數如表1所示[13-14]，其溫度的適用范圍為300 K≤T≤1 100 K。通過MATLAB語言編寫的計算程序可獲得方程式(32)特征值問題的無量綱頻率。首先取節點個數N=17，泊松比μc=0.3，p=0，ΔT=0時，溫度影響下FGM圓環板的面內自由振動問題退化為各向同性圓環板的面內自由振動問題。在表2和表3分別給出了C-C，F-C兩種邊界條件下各向同性材料圓環板振動的無量綱頻率。將計算的結果與已有的研究數據[2,7]進行比較，其結果非常接近，取較少的節點數就能滿足精度所需，工作量較小，說明DQM對于研究本問題的適用性和優越性。

表4和表5分別給出了不同梯度指標p在C-C，F-C邊界條件下，均勻升溫和非均勻升溫時FGM圓環板的前三階頻率。從表中可以看出，頻率Ω隨環向波數n的增大而增大，隨p的增大而減小；在相同參數下，均勻升溫ΔT=800 K時的頻率小于與非均勻升溫ΔTm=0，ΔTc=800 K時相應的頻率。

圖1～圖4分別給出了不同梯度指標p在C-C，F-C邊界條件下，均勻升溫和非均勻升溫時FGM圓環板的一階頻率Ω1與內外半徑比β之間的關系曲線。由圖可見，頻率隨內外半徑比β的增大而單調增大。圖5和圖6分別給出了C-C，F-C邊界條件下均勻升溫時FGM圓環板的前三階頻率Ω與梯度指標p之間的關系曲線。由圖可見，Ω隨p的增大而減小，減小程度由明顯趨于緩慢，當p足夠大時，Ω趨于常數。

圖7～圖8分別給出了不同梯度指標p在F-C邊界條件下，均勻升溫和非均勻升溫時FGM圓環板的前三階頻率Ω與升溫ΔT之間的關系曲線。比較圖7和圖8，不難看出，溫度變化對頻率影響較大。頻率Ω隨升溫ΔT的增大而單調減小，而且升溫相同時，均勻升溫比非均勻升溫對頻率的影響更為顯著，且這種差異程度隨升溫的增大而增大。

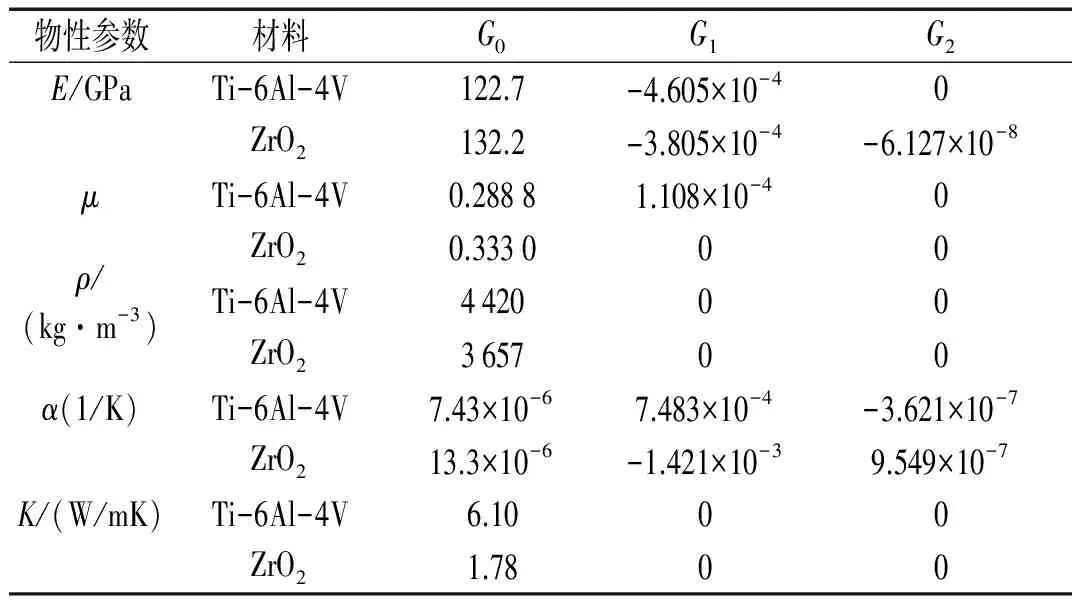
表1 金屬(Ti-6Al-4V)和陶瓷(ZrO2)

表2 圓環板面內自由振動無量綱頻率Ω (C-C)

表3 圓環板面內自由振動無量綱頻率Ω (F-C)

表4 梯度指標p對于FGM圓環板在均勻升溫時前三階無量綱頻率的影響(β=0.2，ΔT=800 K)

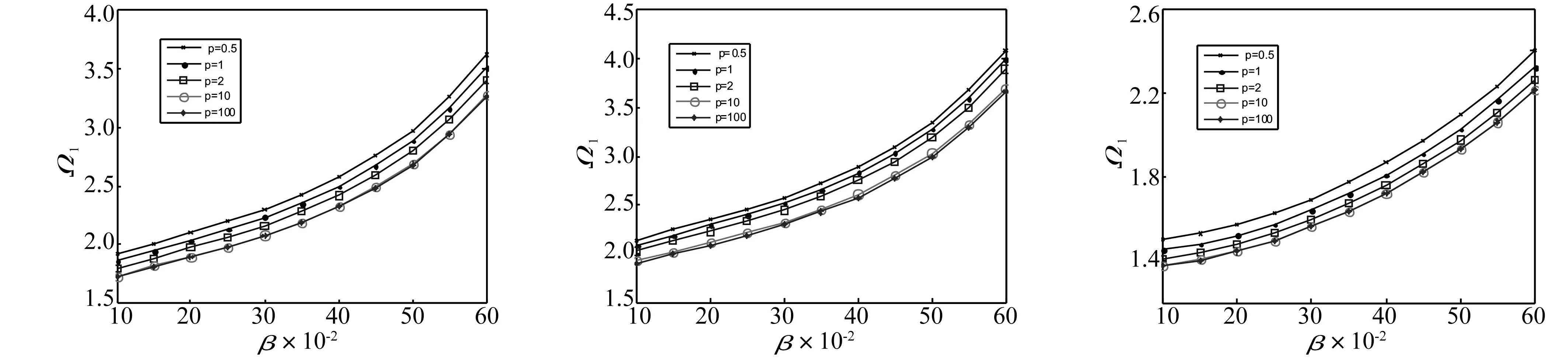
圖1 C-C邊界條件下均勻升溫時一階頻率與內外半徑比之間的關系曲線(ΔT=800K，n=1)Fig．1The1storderdimensionlessnaturalfrequenciesvstheinnertoouterradialratiosubjectedtouniformtemperaturerisewithclampedinnerandouteredges(ΔT=800K，n=1)圖2 C-C邊界條件下非均勻升溫時一階頻率與內外半徑比之間的關系曲線(ΔTm=0，ΔTc=800K，n=1)Fig．2The1storderdimensionlessnaturalfrequenciesvstheinnertoouterradialratiosubjectedtonon?uniformtemperaturerisewithclampedinnerandouteredges(ΔTm=0，ΔTc=800K，n=1)圖3 F-C邊界條件下均勻升溫時一階頻率與內外半徑比之間的關系曲線(ΔT=800K，n=1)Fig．3The1storderdimensionlessnaturalfrequenciesvstheinnertoouterradialratiosubjectedtouniformtemperaturerisewithfreeinnerandclampedouteredges(ΔT=800K，n=1)

圖4 F-C邊界條件下非均勻升溫時一階頻率與內外半徑比之間的關系曲線(ΔTm=0，ΔTc=800K，n=1)Fig．4The1storderdimensionlessnaturalfrequenciesvstheinnertoouterradialratiosubjectedtonon?uniformtemperaturerisewithfreeinnerandclampedouteredges(ΔTm=0，ΔTc=800K，n=1)圖5 C-C邊界條件下均勻升溫時前三階頻率與梯度指標之間的關系曲線(ΔT=800K，β=0．2，n=1)Fig．5Thefirstthreedimensionlessnaturalfrequencyparametersvsmaterialgradedindexsubjectedtouniformtemperaturerisewithclampedinnerandouteredges(ΔT=800K，β=0．2，n=1)圖6 F-C邊界條件下均勻升溫時前三階頻率與梯度指標之間的關系曲線(ΔT=800K，β=0．2，n=1)Fig．6Thefirstthreedimensionlessnaturalfrequencyparametersvsmaterialgradedindexsubjectedtouniformtemperaturerisewithfreeinnerandclampedouteredges(ΔT=800K，β=0．2，n=1)

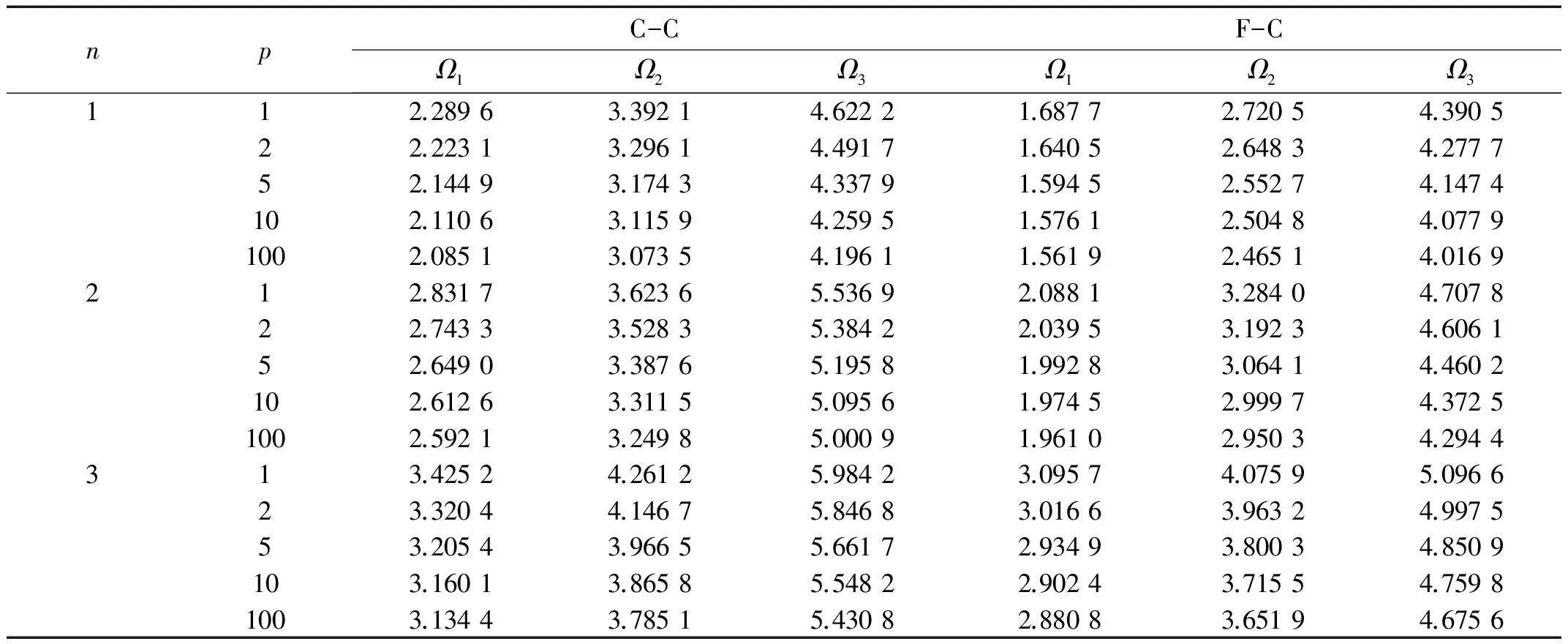
表5 梯度指標p對于FGM圓環板在非均勻升溫時前三階無量綱頻率的影響(β=0.2，ΔTm=0，ΔTc=800 K )

圖7 (a)～(c). F-C邊界條件下均勻升溫時前三階頻率與升溫之間的關系曲線(ΔTc=ΔTm=ΔT，β=0.2,，n=1)Fig.7(a)-(c).The first three dimensionless natural frequency parameters vs uniform temperature rise with free inner and clamped outer edges(ΔTc=ΔTm=ΔT，β=0.2,，n=1)

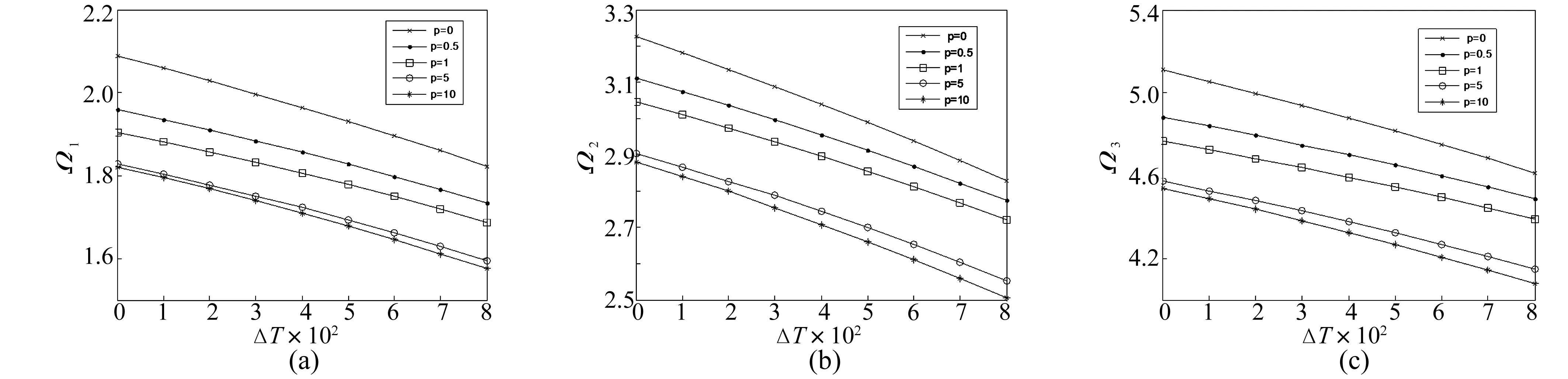
圖8 (a)～(c). F-C邊界條件下非均勻升溫時前三階頻率與升溫之間的關系曲線(ΔTm=0，ΔT=ΔTc，β=0.2，n=1)Fig.8(a)-(c). The first three dimensionless natural frequency parameters vs non-uniform temperature rise with free inner and clamped outer edges(ΔTm=0，ΔT=ΔTc，β=0.2，n=1)

4 結 論

本文基于二維熱彈性理論，研究了溫度影響下FGM薄圓環板的面內自由振動問題。假設材料物性隨溫度變化且沿圓環板徑向按照冪律梯度分布，求得初始熱應力，應用Hamilton原理得出面內自由振動的控制微分方程，用DQM獲得了自由振動的無量綱頻率，并將得到的結果與已有的各向同性材料圓環板頻率進行了比較，說明本文的研究方法有效。最后研究了均勻升溫和非均勻升溫兩種類型下，幾何參數、材料性質和溫度變化對無量綱頻率的影響：頻率隨環向波數的增大而增大；隨內外半徑比的增大而增大；隨梯度指標的增大而減小，減小程度由明顯趨于緩慢，當梯度指標足夠大時，頻率趨于常數；溫度變化對頻率影響較大，且頻率隨溫度的升高而單調減小；均勻升溫與非均勻升溫相比，在相同的邊界條件下升溫相同時，均勻升溫對頻率的影響更為顯著。

[1] 楊志安, 馮宏偉. 電機端蓋超諧共振分析[J]. 工程力學, 2012, 29(10):288-293. YANG Zhi-an, FENG Hong-wei. Superharmonic resonance of end-shields of electric machines [J]. Engineering Mechanics, 2012, 29(10): 288-293.

[2] Irie T, Yamada G, Muramoto Y. Natural frequencies of in-plane vibration of annular plates [J]. Journal of Sound and Vibration, 1984, 97 (1): 171-175.

[3] Farag N H, Pan J. Modal characteristics of in-plane vibration of circular plates clamped at the outer edge [J]. Journal of the Acoustical Society of America, 2003, 113(4): 1935-1946.

[4] 蒲育, 滕兆春, 房曉林. 圓環板面內自由振動的DQM求解[J]. 振動與沖擊, 2013, 32(24): 152-156. PU Yu，TENG Zhao-chun, FANG Xiao-lin. In-plane free vibration of circular annular plates by differential quadrature method[J]. Journal of Vibration and Shock,2013,32(24):152-156.

[5] Tzou K I, Wickert J A, Akay A. In-plane vibration modes of arbitrarily thick disks [J]. Journal of Vibration and Acoustics, 1998, 120(2): 384-391.

[6] Chan II P. Frequency equation for the in-plane vibration of a clamped circular plate [J]. Journal of Sound and Vibration, 2008, 313(1-2,3): 325-333.

[7] Bashmal S, Bhat R, Rakheja S. In-plane free vibration of circular annular disks [J]. Journal of Sound and Vibration, 2009, 322(1-2): 216-226.

[8] Bashmal S, Bhat R, Rakheja S. In-plane free vibration analysis of an annular disk with point elastic support [J]. Shock and Vibration, 2011, 18(4): 627-640.

[9] Aletkin M. Free in-plane vibration of super-elliptical plates [J]. Shock and Vibration, 2011, 18(3): 471-484.

[10] Ma L S, WANG T J.Nonlinear bending and post-buckling of a functionally graded circular plate under mechanical and thermal loadings [J]. International Journal of Solids and Structures, 2003, 40(13-14): 3311-3330.

[11] Ma L S,Wang T J. Relationships between axisymmetric bending and buckling solutions of FGM circular plates based on third-order plate theory and classical plate theory [J]. International Journal of Solids and Structures, 2004, 41(1): 85-101.

[12] Nie G J, Zhong Z. Semi-analytical solution for three-dimensional vibration of functionally graded circular plates [J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(49-52): 4901-4910.

[13] Touloukian Y S. Thermophysical properties of high temperature solid materials [M]. New York: MacMillan, 1967.

[14] Kim Y W. Temperature dependent vibration analysis of functionally graded rectangular plates [J]. Journal of Sound and Vibration, 2005, 284(3-5): 531-549.

[15] Prakash T. Ganapathi M. Asymmetric flexural vibration and thermoelastic stability of FGM circular plates using finite element method [J]. Composite Part B: Engineering, 2006, 37(7-8): 642-649.

[16] Bert C W, Malik M. Differential quadrature method in computational mechanics: A Review [J]. Applied Mechanics Reviews, 1996, 49(1): 1-28.

In-plane free vibration of FGM annular plates considering temperature effect

TENG Zhao-chun, PU Yu

(College of Science, Lanzhou University of Technology, Lanzhou 730050, China)

Based on the two-dimensional elastic theory and the Hamilton’s principle, the differential motion equations for in-plane free vibration of the functionally graded material thin annular plate in thermal environment were derived. In the equations, the material properties were assumed to be temperature-dependent and graded in the radial direction of annular plates according to power law distributions. By using differential quadrature method(DQM), the dimensionless frequency parameters of in-plane free vibration of FGM annular plates under thermal environment were obtained. The formulations were validated by comparing the results with those available in literatures. Considering the cases of uniform and variable temperature rise distribution in the radial direction of annular plate respectively, the effects of geometrical parameters, material graded index and temperature rise on the natural frequencies of in-plane free vibration of annular plates were investigated.

FGM (Functionally Graded Material) annular plates; initial thermal stress; in-plane free vibration; dimensionless frequency; Hamilton’s principle; DQM

國家自然科學基金項目(11372123)

2013-10-29 修改稿收到日期：2014-05-29

滕兆春 男，碩士，副教授，1969年8月生

O343

A

10.13465/j.cnki.jvs.2015.09.037