雙限位器隔離系統的沖擊響應計算及參數影響分析

張春輝， 汪 玉， 吳一紅， 溫肇東

(1. 海軍工程大學 動力工程學院，武漢 430033； 2. 海軍裝備研究院，北京 100161)

雙限位器隔離系統的沖擊響應計算及參數影響分析

張春輝1， 汪 玉2， 吳一紅2， 溫肇東2

(1. 海軍工程大學 動力工程學院，武漢 430033； 2. 海軍裝備研究院，北京 100161)

針對限位器在承受沖擊載荷過程中存在二次沖擊的問題，建立了雙限位器沖擊隔離系統數學模型，通過分段線性的杜哈梅積分對沖擊方程進行了解析求解，并與階躍速度法的沖擊響應結果進行對比，分析限位器參數(剛度比、阻尼比、安裝間隙)對沖擊響應的影響，討論了多島遺傳算法在限位器參數優化中的應用。研究結果表明：適當的限位器阻尼可以有效提升隔沖系統的抗沖擊能力，但當阻尼較大時，不可用速度階躍法進行計算；制定合理的優化策略，利用多島遺傳算法可以得到符合沖擊要求的限位器最優參數。

限位器；杜哈梅積分；階躍速度法；多島遺傳算法

船舶在服役期間必然要面臨接觸性爆炸、非接觸性爆炸及自身武器發射等帶來的強沖擊問題[1]。船舶設計時對大多數機械設備采用了隔振裝置兼著沖擊防護作用。這種隔振裝置雖然可以減小設備的絕對加速度響應幅值，但卻會產生較大的相對位移，設備相對位移過大有可能造成設備附屬連接管系的損壞，甚至超過隔振器本身的極限變形能力[2]。目前，為了改善這種情況，通常在隔振系統中安裝限位器，此種方法可以降低相對位移幅值，但如果所取限位參數不合理，卻會引起系統的二次沖擊問題[3-4]。因此，對限位器的參數影響和優化設計研究具有重要意義。文獻[5]對限位器隔沖系統的沖擊響應進行了計算，探討了限位器各參數對抗沖擊性能的影響，并提出了限位器參數的確定方法，文獻[6]利用有限元及遺傳算法優化設計得到了剛度分段線性隔沖系統的最優解集，文獻[7]利用有限元法研究了彈性限位器的剛度和安裝間隙對雙層隔振裝置抗沖擊性能的影響，以上研究為限位器的實際應用提供了理論基礎，但都忽略了限位器阻尼對抗沖擊作用的影響。文獻[8]雖然考慮了有阻尼限位器隔沖系統的沖擊響應計算和參數影響分析，但計算時把沖擊激勵信號簡化為速度階躍信號，忽略了沖擊作用過程中阻尼的粘滯作用，使得系統一開始就獲得初速度，可能會對系統造成誤差。

本文首先建立了雙限位器沖擊隔離系統數學模型，通過分段線性的杜哈梅積分對沖擊方程進行了解析求解。然后用數值方法分析了限位器參數對沖擊響應的影響，并與階躍速度法的沖擊響應結果進行了對比。最后用多島遺傳算法優化設計了限位器參數。

1 含雙限位器隔沖系統數學模型及求解

含雙限位器的沖擊隔離系統如圖1所示，隔振器彈簧的支撐剛度為k，限位器彈簧的剛度為ka，限位器安裝間隙為D0，模擬設備質量塊為m，隔振器阻尼系數為c，限位器阻尼系數為c1。令相對位移x(t)=z(t)-u(t)，當系統基礎受到沖擊激勵時，可以得到運動微分方程：

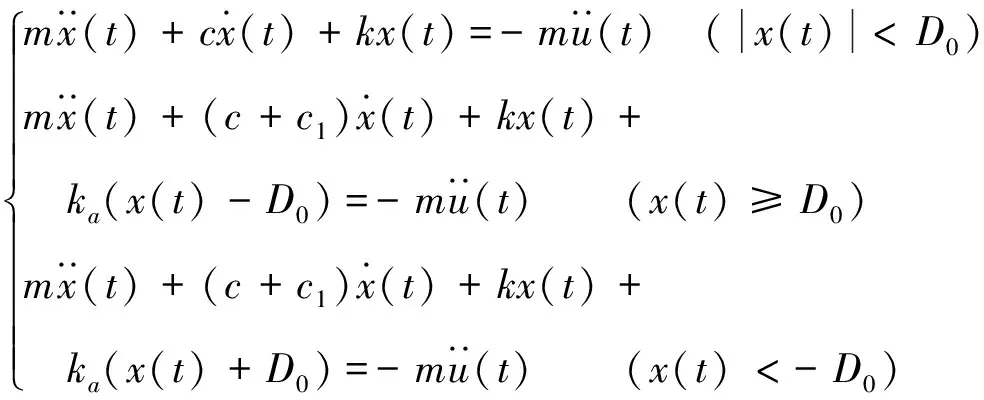
(2)

式中:A是加速度幅值，ωs是激勵信號角頻率，t0是沖擊持續時間。

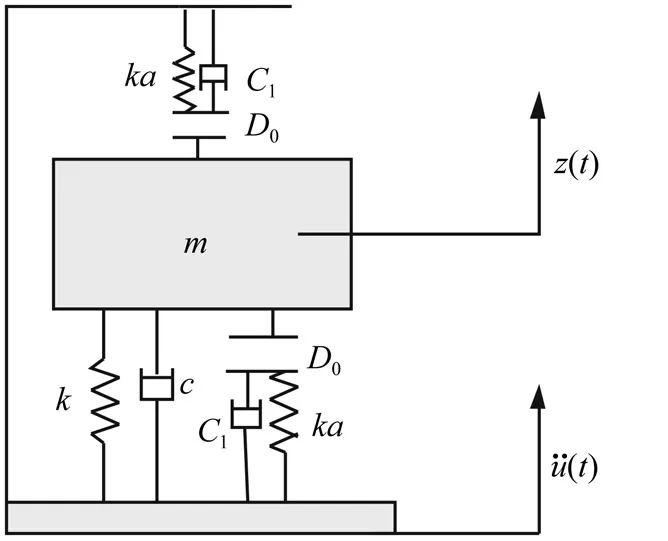
圖1 雙限位器沖擊隔離系統Fig.1 Shock isolation system with double displacement restrictors

沖擊響應一般分為兩個階段：沖擊載荷作用階段和沖擊載荷作用結束后的殘余響應階段。由于兩個階段受到的沖擊激勵不同，且兩個階段各時間段的等效剛度也不同，故采取分段線性化的方法進行求解。

(1) 沖擊載荷作用階段

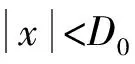
(3)

(4)

進一步，由微分方程組(1)第一式可推得被隔離設備的絕對加速度

(5)

(6)

對上式采用杜哈梅積分可得：

(7)

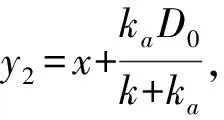
(8)

對上式采用杜哈梅積分可得：

(2) 殘余響應階段的沖擊響應

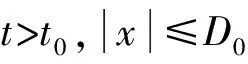
(10)

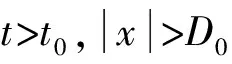
(11)

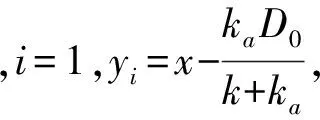
2 限位器參數對沖擊響應的影響分析

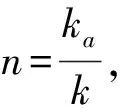
不同剛度比下設備的絕對加速度響應幅值與阻尼比的關系如圖2所示。從圖中可以看出，對于某一確定的剛度比，存在一個最佳阻尼比使得絕對加速度響應幅值最小，且剛度比越大，最佳阻尼比值越大；當阻尼比大于最佳阻尼比后，不同剛度比下的絕對加速度響應幅值與阻尼比近似呈線性關系，且斜率相同。

不同剛度比下相對位移幅值與阻尼比的關系曲線如圖3所示。從圖中可以看出，對于任意確定的剛度比，阻尼比越大，相對位移響應幅值越小，特別是當阻尼比小于0.4，剛度比n<5時，相對位移幅值隨著阻尼比的衰減比較明顯。

為了綜合評價隔沖系統的抗沖擊性能，在沖擊響應過程中，一般用緩沖系數表示系統的抗沖擊極限性能，其值越小，表示系統抗沖性能越好。系統緩沖系數η計算公式為

(12)

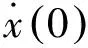
不同剛度比下系統緩沖系數隨阻尼比的變化曲線如圖4所示。從圖中可以看出，對于不同的剛度比，緩沖系數隨著阻尼比的增大先減小后增大，即存在一個最優阻尼比使得緩沖系數最小，且剛度比越大，最優阻尼比值越大。結合圖2和圖4可以看出，對于同一剛度比，最優阻尼比值稍大于最佳阻尼比值，這主要是因為沖擊響應過程中相對位移響應幅值隨著阻尼比的增大不斷減小。

雙限位器沖擊隔離系統的沖擊響應與安裝間隙的關系如圖5～7所示。從圖中可以看出，相對位移響應幅值與安裝間隙近似呈正比，絕對加速度響應幅值則與安裝間隙近似呈反比，安裝間隙增大，絕對加速度響應幅值迅速減小。系統緩沖系數則隨著安裝間隙的增大先增大后減小。限位器實際設計時，應避開使緩沖系數最大的安裝間隙，且安裝間隙在大于振動幅值的前提下應盡量減小。

圖2 不同剛度比下絕對加速度幅值隨阻尼比的變化曲線Fig．2Absoluteaccelerationvs．dampingratioandstiffnessratio圖3 不同剛度比下相對位移幅值隨阻尼比的變化曲線Fig．3Relativedisplacementvs．dampingratioandstiffnessratio圖4 不同剛度比緩沖系數隨阻尼比的變化曲線Fig．4Buffercoefficientvs．dampingratioandstiffnessratio

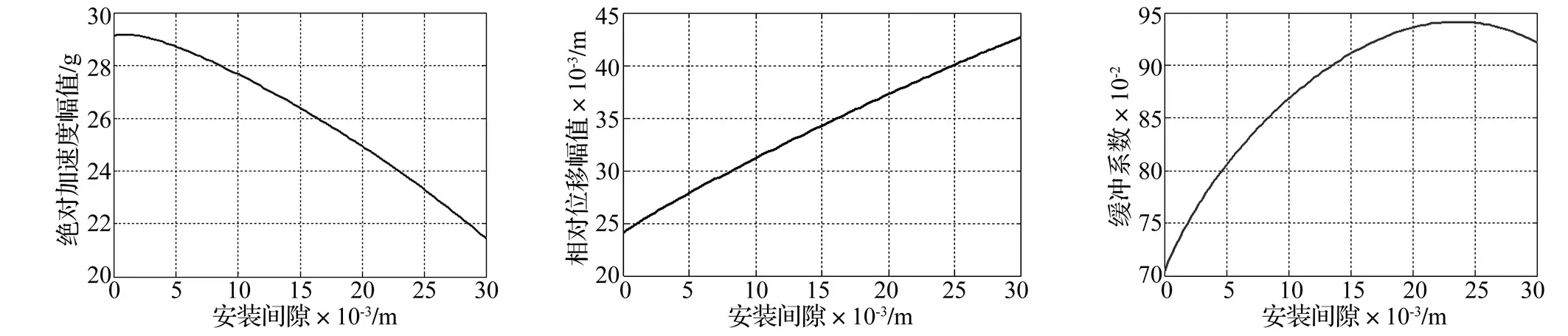
圖5 絕對加速度與安裝間隙的關系Fig．5Absoluteaccelerationvs．installationclearance圖6 相對位移幅值與安裝間隙的關系Fig．6Relativedisplacementvs．installationclearance圖7 緩沖系數與安裝間隙的關系Fig．7Buffercoefficientvs．installationclearance

3 速度階躍等效對沖擊響應的影響

傳統上，當沖擊作用時間遠小于系統固有周期時，通常把沖擊激勵理想化為階躍速度，即

(13)

速度階躍等效后運動微分方程組(1)變成齊次微分方程，大大簡化了沖擊響應計算，但這種簡化方式忽略了沖擊脈寬及粘滯阻尼作用的影響，對沖擊響應結果會造成誤差。通過對不同剛度比和不同阻尼比沖擊模型進行仿真計算，分析階躍速度等效法對沖擊響應的影響。

圖2～4的仿真結果沒有進行階躍速度等效，保存了系統的真實特性，可以將其作為其他仿真結果的標尺。階躍速度等效法得到的沖擊響應結果如圖8～10所示。對比兩組仿真圖可以看出，當阻尼比大于0.5時，階躍速度等效法計算得到的加速度響應峰值和緩沖系數過大，偏離了真實值；相對位移響應幅值近似相等。因此，當阻尼比大于0.5時階躍速度等效法不適用于求解帶限位器的剛度非線性微分方程。

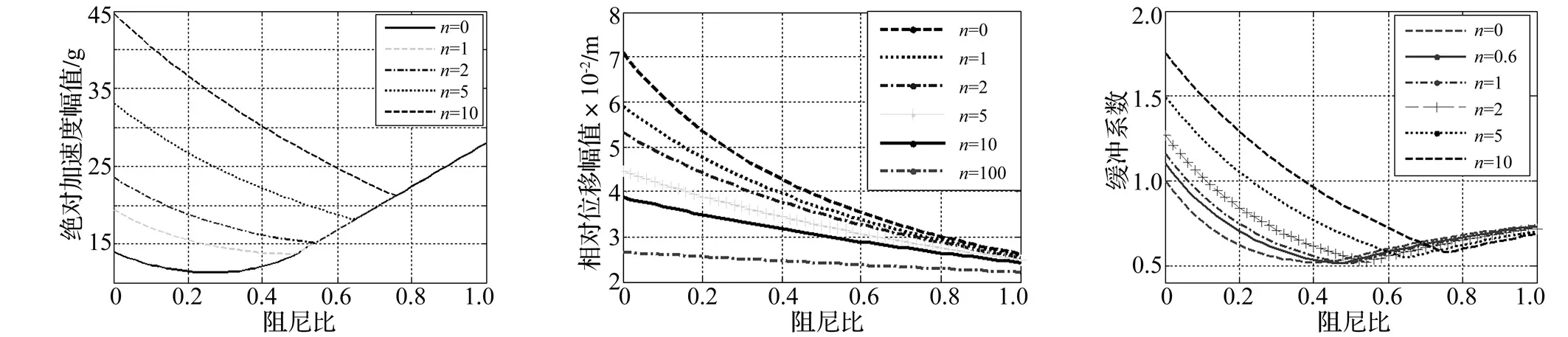
圖8 階躍速度時絕對加速度幅值隨剛度比和阻尼比的變化Fig．8Amplitudeofabsoluteaccelerationvs．dampingratioandstiffnessratiowithvelocitystepequivalent圖9 階躍速度時相對位移幅值隨剛度比和阻尼比的變化Fig．9Amplitudeofrelativedisplacementvs．dampingratioandstiffnessratiowithvelocitystepequivalent圖10 階躍速度時緩沖系數隨剛度比和阻尼比的變化Fig．10Thebuffercoefficientvs．dampingratioandfrequencyratiowithvelocitystepequivalent

4 限位器參數優化設計

4.1 優化方法

遺傳算法是根據生物進化思想啟發得出的一種全局優化算法，而多島遺傳算法是在此基礎上發展起來的一種偽并行遺傳算法[9]。其特點是將整個進化群體劃分為若干子群體(島嶼)，在每個島嶼上對子群體獨立地進行傳統遺傳算法的選擇、交叉、變異等遺傳操作。多島遺傳算法采用的輪盤賭選擇法和精英保留策略，保證了將父代中的最佳個體復制到子代中，定期隨機選擇一些個體進行“遷移”操作，將其轉移到別的島嶼上，通過這種方式,可以維持群體的多樣性，從而抑制了早熟現象[10]。

4.2 優化策略及參數選擇

隔振裝置設計時，系統的支撐剛度k主要根據系統隔振要求(固有頻率)確定；限位器參數則根據限位器的使用情況和抗沖擊要求綜合確定。基于此，限位器參數按照以下三種策略進行優化：一是根據設備允許承受的最大加速度確定一個加速度閾值(略小于設備允許承受的最大加速度幅值)，通過最小化相對位移響應幅值的方法來確定限位器的參數。二是根據隔振器和外接管路允許的最大變形量確定一個相對位移閾值(取二者中較小者)，通過最小化設備的絕對加速度響應幅值來確定限位器的各項參數。三是給出設備能夠承受的加速度范圍和相對位移范圍，通過最小化緩沖系數的方式獲得限位器的最優參數。

采用多島遺傳算法分別對上述3種策略下限位器的參數進行優化。計算過程中，種群數、島數和進化代數均選擇10，目標函數分別為

MINf1(X)=x(t,D0,ξc1,n)

(14)

(15)

MINf3(X)=η(t,D0,ξc1,n)

(16)

式中;f1(X)、f2(X)、f3(X)分別代表三種優化目標：相對位移、絕對加速度和緩沖系數，X代表優化變量向量。優化變量范圍和約束條件如表1所示。

表1 遺傳算法參數

4.3 優化結果

為檢驗多島遺傳算法的優化結果，根據第二部分的分析，為限位器選擇一組初始參數，與優化結果進行對比。文獻[11]中提出線性剛度系統存在最佳阻尼比0.265，故選擇阻尼比ξc1=0.265為初始條件，另隨機選取初始條件D0=5 mm，n=3。

限位器的優化參數及沖擊響應結果如表2所示。從表2可以看出，三種優化策略的結果均在設計變量范圍內，且都滿足約束條件；與限位器初始參數相比，第一種優化策略產生的相對位移響應幅值下降12.3 mm，第二種優化策略產生的絕對加速度響應幅值下降6 g；第三種優化策略產生的緩沖系數下降0.242。

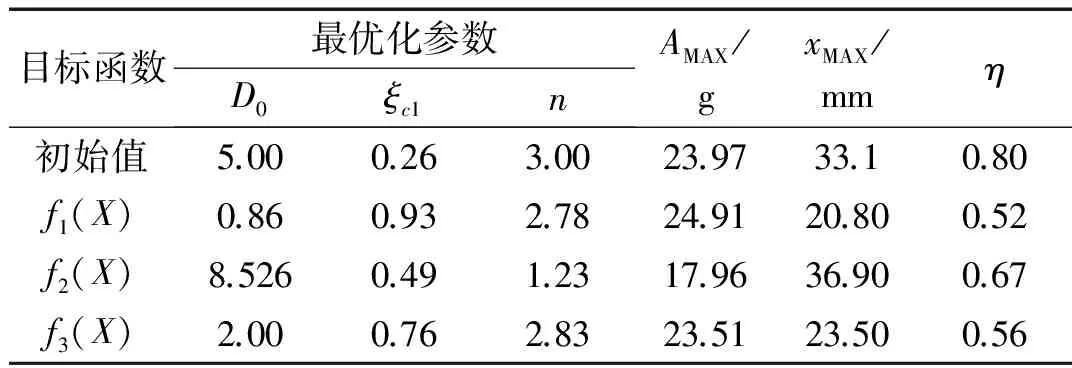
表2 優化參數及沖擊響應結果

5 結 論

利用杜哈梅積分對雙限位器沖擊隔離系統運動方程進行解析求解；分析限位器參數(剛度比、阻尼比、安裝間隙)對系統抗沖擊性能的影響；應用多島遺傳算法對限位器參數進行了三種策略的優化，并與階躍速度等效法進行對比，主要結論有：

(1) 對于任意確定的剛度比，存在一個最佳阻尼比使得絕對加速度響應幅值最小，且剛度比增大，最佳阻尼比增大；

(2) 當阻尼比大于最佳阻尼比時，對于任意剛度比，加速度幅值與阻尼比近似成線性關系；

(3) 對于任意確定的剛度比，存在一個最優阻尼比使得系統緩沖系數最小，當阻尼比大于該最優阻尼比時，緩沖系數隨著阻尼比的增大緩慢增加；

(4) 當限位器阻尼比大于0.5時，階躍速度等效法不適于求解帶限位器的沖擊微分方程；

(5) 根據限位器的使用要求，可以通過多島遺傳算法得到限位器的最優參數。

[1] Scavuzzo R J，Pusey H C. Naval shock analysis and design [M]. Falls Church：The Shock and Vibration Information Analysis Center，2000.

[2] 汪 玉, 華宏星. 艦船現代沖擊理論及應用[M]. 北京: 科學出版社, 2005:1-68．

[3] 張志，張兆會，董森，等.橡膠雙層減振與隔振系統沖擊響應研究[J].振動與沖擊,2013,32(23):126-129. ZHANG Zhi,ZHANG Zhao-hui,DONG Sen,et al.Shock response of a rubber double-deck vibration isolation system[J].Journal of Vibration and Shock,2013,32(23): 126-129.

[4] Rudolph J S，Henry C P. Naval shock analysis and design [M]. The Shock and Vibration Information Analysis Center Booz，Allen and Hamilton, inc. USA, 2000.

[5] 趙應龍，何琳，黃映云，等. 限位器對隔振系統抗沖擊性能的影響[J]. 振動與沖擊，2005，24(6)：71-76. ZHAO Ying-long, HE Lin, HUANG Ying-yun, et al. Influence of the displacement restrictor on shock resistance performance of vibration isolation system [J]. Journal of Vibration and Shock, 2005,24(6): 71-76.

[6] 唐斯密，趙存生，朱石堅. 剛度分段線性系統隔振抗沖擊優化設計研究[J]. 噪聲與振動控制，2010,30(1)：27-32. TANG Si-mi, ZHAO Cun-sheng, ZHU Shi-jian. Study on optimal design for vibration and shock isolation of piecewise linear stiffness system[J]. Noise and Vibration Control,2010,30(1): 27-32.

[7] 馬炳杰，沈建平，王志剛. 彈性限位器對雙層隔振裝置抗沖擊性能影響分析[J]. 噪聲與振動控制，2011,31(6)：72-75. MA Bing-jie, SHEN Jian-ping, WANG Zhi-gang. Affect of displacement restrictor on shock resistance performance of double-stage vibration isolation system[J].Noise and Vibration Control, 2011, 31(6): 72-75.

[8] 翁雪濤，朱石堅，何琳. 限位器抗沖擊計算[J]. 中國造船，2002，43(2)：85-89. WENG Xue-tao, ZHU Shi-jian, HE Lin.Calculation of shock resistance performance of restrictor[J]. Ship Buliding of China, 2002, 43(2): 85-89.

[9] 石秀華, 孟祥眾, 杜向黨. 基于多島遺傳算法的振動控制傳感器優化配置[J]. 振動、測試與診斷, 2008(1): 62-65. SHI Xiu-hua, MENG Xiang-zhong, DU Xiang-dang. Application of MIGA to optimal disposition of sensors in active control [J].Journal of Vibration, Measurement & Diagnosis, 2008(1): 62-65.

[10] 宋昕, 谷正氣, 張清林. 基于多島遺傳算法的湍流模型優化研究[J]. 湖南大學學報(自然科學版)，2011, 38(2): 23-29. SONG Xin, GU Zheng-qi, ZHANG Qing-lin.Study of the turbulence model optimization based on multi-island genetic algorithm[J]. Journal of Hunan University(Natural Sciences), 2011, 38(2): 23-29.

[11] 單樹軍，何琳. 粘性阻尼在硬特性剛度隔沖系統中的作用[J]. 振動與沖擊，2008，27(6)：96-98. SHAN Shu-jun, He Lin. Effect of viscous damping in a harden stiffness shock isolation[J]. Journal of Vibration and Shock, 2008，27(6)：96-98.

Shock response calculation and effects of structural parameters on shock isolation system with double displacement restrictors

ZHANG Chun-hui1, WANG Yu2, WU Yi-hong2, WEN Zhao-dong2

(1. Naval University of Engineering, Wuhan 430033, China; 2. Naval Academy of Armament, Beijing 100161, China)

In order to solve the secondary impact problem of displacement restrictors in the process of enduring impact load, the mathematical model of a shock isolation system with double displacement restrictors was established. The analytical solution for the shock isolation system was obtained by using a piecewise linear Duhamel integral method, and compared with the results by using the step velocity method. Effects of displacement restrictors’ parameters (stiffness ratio, damping ratio and assembled clearance) on shock responses were studied and the application of multi-island genetic algorithm in parameter optimization was discussed. The results prove that proper damping ratio of displacement restrictor can provide effective impact resistance to the system, but the equations could not be solved by the step velocity method in large damping ratio condition. Besides, by using multi-island genetic algorithm, the optimal parameters of displacement restrictor can be adjusted to meet shock isolation requirement by proposing reasonable optimization strategy.

displacement restrictors; Duhamel integral; step velocity method; multi-island genetic algorithm

973項目(613157010102)；十二五預研基金(4010304030202)

2014-08-26 修改稿收到日期：2014-11-06

張春輝 男，博士，1988年生

汪玉 男，博士，研究員，博士生導師，1964年生

O322

A

10.13465/j.cnki.jvs.2015.09.023