美式期權定價的一種蒙特卡洛方法

張麗虹

（云南財經大學馬克思主義學院，昆明 650221）

引言

在最近的幾十年里，金融衍生市場的發展已經成為影響經濟的重要現象，衍生市場是相對于基礎市場而言的。金融衍生物是一種風險管理工具，它的價值依賴于基本的原生資產（或稱標的資產）的價格變化。在金融市場，商品市場有很多形式的金融衍生工具，其中遠期合約、期貨和期權是三種最基本的金融衍生工具。如果把原生資產設定為股票、債券、匯率或商品等，那么為了對這些原生資產進行風險管理，相應的有：股票期貨（期權）、債券期貨（期權）、貨幣期貨（期權）以及商品期貨（期權）等[3，7]。

在市場經濟發達的國家，期權市場已是構成其證券市場的一個重要組成部分。近二十年來，國際金融界對期權理論的研究和應用投入了巨大的關注。特別是在西方發達國家，期權理論的發展日新月異，期權應用研究也緊隨其后[3，7]。從金融期權研究得出的原理、方法和結論不僅僅應用于期權投資領域，還可以廣泛應用于宏觀、微觀經濟和管理問題的分析與決策[8]。瑞典皇家科學院將1997年度的諾貝爾經濟學獎授予兩位對現代期權理論研究有突出貢獻的經濟學家：美國斯坦福大學教授梅隆·舒爾斯（Myron Scholes）和哈佛大學教授羅伯特·莫（Robert C.Merton），這表明全世界對期權理論研究和實際應用重要性的認可[5，7]。由于歷史、體制、學科建設等方面因素的影響制約，期權理論在我國的研究才剛剛開始，其應用也幾乎呈空白狀態。但我國政府、金融學術界和實務界已經越來越重視這一理論的研究和應用。國務院曾多次指示要加快金融科學的設立，國家自然科學基金會對金融數學、金融工程的研究項目支持力度也較大。現在已有相當一部分學者正活躍在這一領域，許多大學相繼成立了金融數學系和金融工程中心，并開始了相應的學術研究和人才培養工作，這將對中國的金融改革，特別是金融數學、金融工程的發展做出有益的嘗試和貢獻。期權理論作為金融數學的一個重要研究內容也將得到迅速的發展。隨著中國經濟市場化進程的發展和各方面條件的成熟，期權市場在中國的發育和發展是中國市場體系，特別是金融市場發展與完善過程中的一項重要內容，是大勢所趨[1]。

期權是最重要的金融衍生工具之一，合理定價則是期權發揮其功能的基礎。對于歐式期權，已經有了經典的Black-Scholes公式，但由于美式期權具有可提前執行的特性，Black-Scholes公式并不適用[7]。

期權作為一種衍生金融產品，它的價格決定于標的資產價格的變化。標的資產的價格變化是不確定以及隨機的，所以由此產生的期權價格變化也是隨機的。但是一旦標的資產的價格確定下來，那么作為其衍生物的期權的價格也將隨之確定，即存在函數Vt=V（St，t）。它表示若在t時刻原生資產的價格為 St，則期權的價格為 Vt=V（St，t）。這里的期權價格V（St，t）是一個確定的二元函數。通常在期權的到期日那天，期權的價值（或成為期權的收益、期權的價格）V（St，t）是確定的。但是期權生效日t=0那天的期權價格即期權金是未知的。因為他是期權購買者為了取得這個未定權益所要付出的代價。我們的計算目的就是求出期權金的值[1]。

通常計算美式期權的方法有有限差分法、二叉樹法及蒙特卡洛法[2，6，9]。本文將討論如何利用蒙特卡洛方法來計算美式期權的價格。國內學者在考慮美式期權定價問題的蒙特卡洛方法時，比較少詳細討論方法的具體設計過程[6，9-12]，并且由于美式期權一般不具有封閉解，所以人們通常依靠數值解法來解決這一問題。本文將詳細討論方法的設計過程，并用Matlab程序在計算機上數值實現該過程。本文將按照下面的方式來組織：（1）簡單介紹美式期權的定義、美式期權的特性及分類等基本概念，幫助人們更好地理解美式期權；（2）詳細討論美式期權定價的蒙特卡洛方法設計與數值計算過程；（3）得出計算結果并與傳統的有限差分法計算得到的結果相比較。

一、美式期權的基本概念

美式期權是指可以在成交后有效期內任何一天被執行的期權。也就是指期權持有者可以在期權到期日以前的任何一個工作日，選擇執行或不執行期權合約。它通常分為美式看漲期權與美式看跌期權。

美式看漲期權在行權期內，如果標的資產S高于敲定價格K，則持有者隨時可以以敲定價格K買進標的資產。此時持有者以價格K買入標的資產，在市場中又可以以即時價格S賣出，獲得利潤S-K；若在行權期內，標的資產的價格始終低于敲定價格K，則持有者可以選擇不買進任何標的資產，此時獲得的利潤為0，所以看漲期權的最終價格是確定的：V（S，t）=max（S-K；0）。

美式看跌期權在行權期內，如果標的資產價格S低于敲定價格K，則持有者隨時可以以敲定價格K賣出標的資產，獲得利潤K-S；若在行權期內，標的資產的價格始終高于敲定價格K，則持有者可以選擇不賣出任何標的資產，此時獲得的利潤為0，所以看跌期權的最終價格是確定的：V（S，t）=max（K-S；0）。

二、美式期權定價的蒙特卡洛方法

首先假定美式期權標的資產的價格，也就是S=S（t）服從下面的隨機過程：

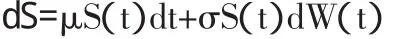
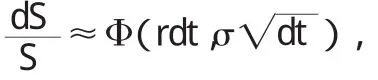
對于任意的t>0都成立，這里z是服從標準正態分布隨機變量（均值0，方差1）。在下面的蒙特卡洛方法計算中，我們就是利用公式（1）來模擬標的資產在任意t時刻的價格。

下面討論蒙特卡洛方法計算在t=0時刻美式期權的價格。設t=T是美式期權交割日時間，t=0是美式期權開始生效的那一時刻，S（t）表示美式期權標的資產在t時刻的價格。假定 t0，t1，t2，…，tm滿足：

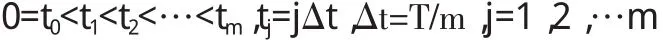
且記Si=S（ti），i=0，1，2，…，m；這里的m是一個給定的正整數。同時假定美式期權只可能在t1，t2，…，tm這m個有限時刻行權。下面，可以記Vi（s）表示在t=ti時刻且標的資產的價格Si=s時美式期權的價格。并且記hi（s）=h（Si=s），這里規定：

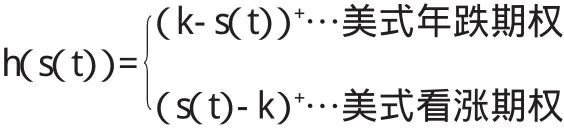
如果r（t）是一個常函數，例如r（t）=r不變，則Di-1，i=e-r（ti-ti-1），若進一步規定 ti=iΔt，i=0，1，2，…m則：

本文首要的計算目的是求出V0（s）的值，也即在t=0時刻且標的資產價格S0=s時美式期權的價格。關于它的計算，可以用下面的公式來計算：

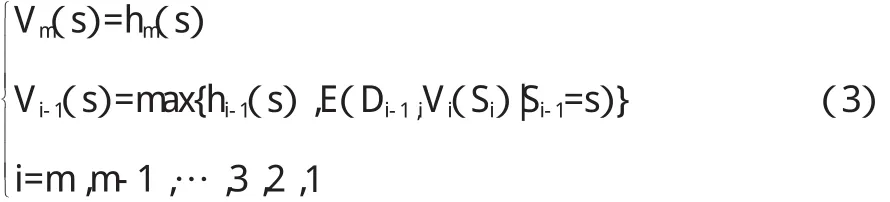
如果對所有的 i=1，2，…m，有 Di-1，i=e-rΔt，則：

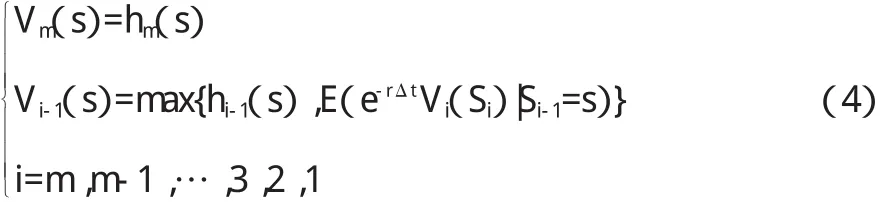
這里的E（e-rΔtVi（Si）|Si-1=s）代表一條件數學期望。

為了便于（4）的計算，我們引入新的變量：

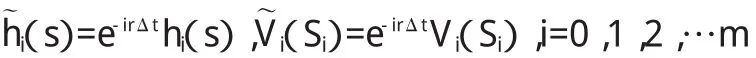
通過計算，（4）可變化為：

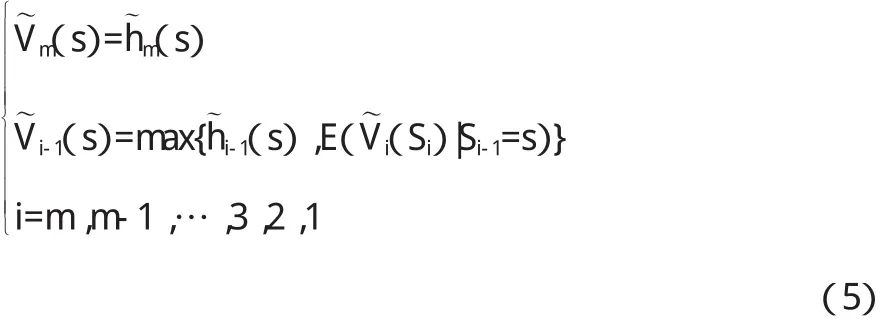
為了順利進行下一步的計算，首先要求出（5）中的條件期望E（i（Si）|Si-1=s）。為此，我們假定：

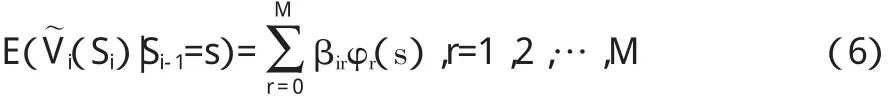
這里，φ1（s），φ2（s），…，φM（s）是一些形式已知的基函數。在后面的計算之中，本文選取以下基函數：φr（s）=sr，r=0，1，2，…，M。由（6）可得：

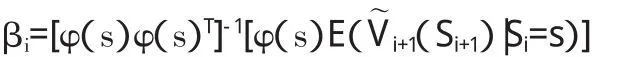
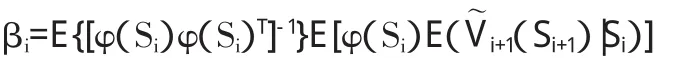
蒙特卡洛方法主要利用（5）式計算V0（s），該方法通過以下步驟分步進行：

1.給定 S（0）=s的值。

2.根據式（1），先模擬 n條標的資產價格 S（t）變化的曲線，每條曲線上都有m個值，也即t1，t2，…，tm時刻的值為{S1j，S2j，…，Smj}，j=1，2，…，n。

4.對于 i=m-1，…3，2，1，0按照下列步驟進行循環計算：

三、計算結果

我們假定用有限差分法計算出來的結果為“準確解”（該方法詳細內容見[13]之中的介紹），然后將其與蒙特卡洛方法得出的結果進行比較分析。

在具體的計算過程中，本文設標的資產的平均收益率r=0.1，標的資產波動率σ=0.4，到期日T=1（年），合約執行價格K=10。

關于美式看跌期權，t=0時的價格V0（s）對不同的s計算結果（見下頁表1）。

關于美式看漲期權，t=0時的價格V0（s）對不同的s計算結果（見下頁表2）。

從表2中不難看出，模擬次數越多時，得到的數值解越接近“準確解”。

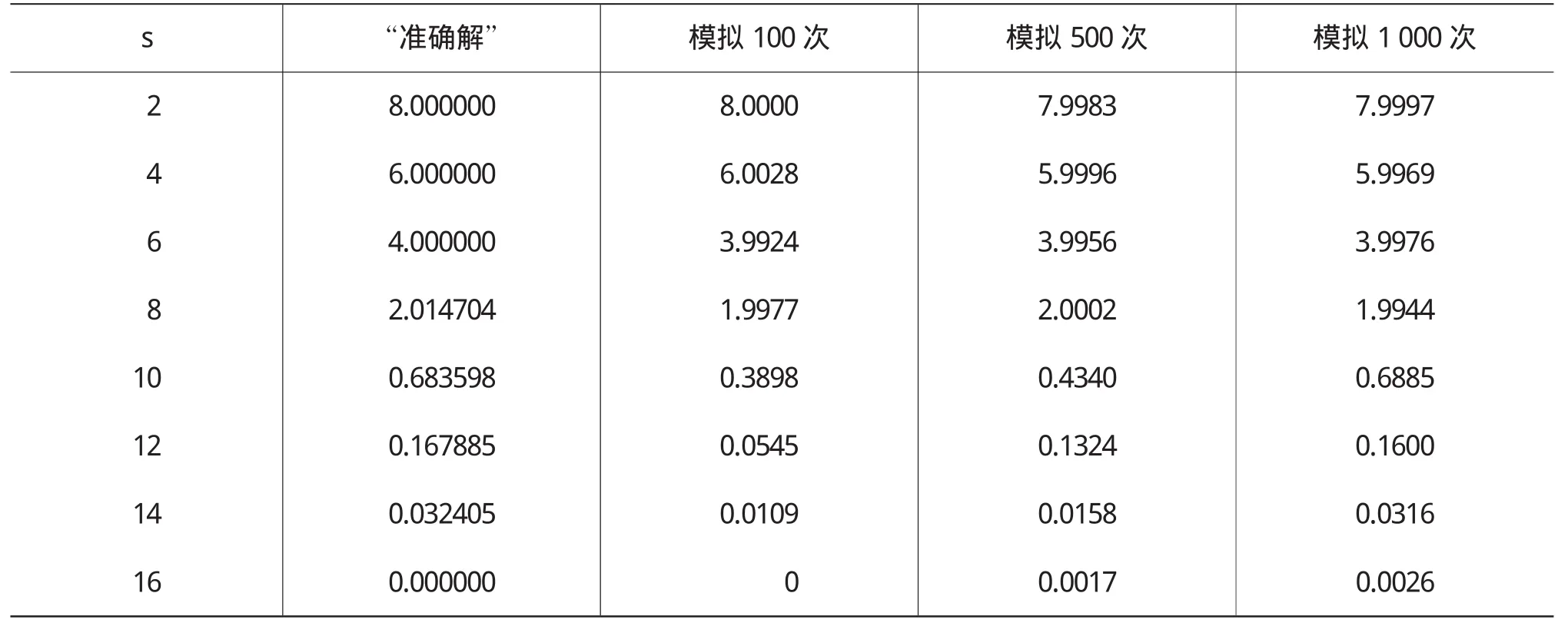
表1

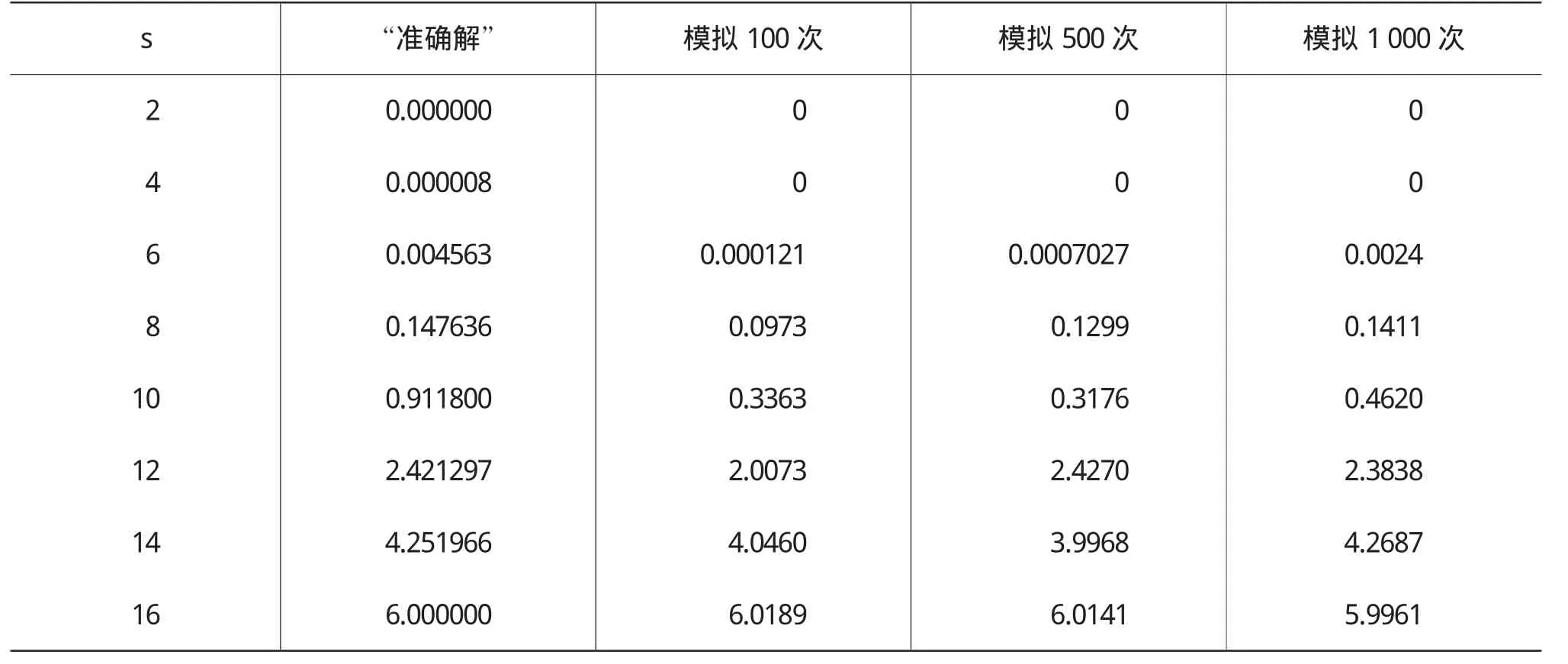
表2

結論

本文討論了美式期權定價的蒙特卡洛方法，我們根據美式期權的特點詳細地制定了相應的數學模型和Matlab程序。本文比較了蒙特卡洛方法與有限差分法得到的數值結果，發現它們非常接近。相對于傳統二項式、有限差分（隱式和顯式）等方法，蒙特卡洛方法具備了更好的普適性，可推廣用于各式期權價格的計算中，在實際應用中也就更能大顯身手。但蒙特卡洛方法也有自己的缺點，那就是仿真結果不太精確，具有較大波動性，尤其是在在模擬次數較小的時候。為了提高精度，我們可以增加模擬次數。但是，蒙特卡洛方法具有一般性，相信本文的研究方法可以較好地解決其他各式期權價格的計算問題，同時，也可以將之推廣應用于其他類型的金融衍生品的定價問題中。

[1]姜禮尚.期權定價的數學模型和方法[M].北京：高等教育出版社，2003.

[2]林群.微分方程數值解法基礎教程：第2版[M].北京：科學出版社，2003.

[3]Robert.Tompkins.解讀期權：第2版[M].陳宋生，崔宏，劉鋒，譯.北京：經濟管理出版社，2004.

[4]Longstaff，Schwartz ES.Valuing American optionsby simulationasimpleleast squaresapproach[J].Reviewof Financial Studies，2001，(1)：113-148.

[5]F.Black，M.Scholes，The pricing of options and corporate liabilities，J.Polit.Econ，1973，(3)：637-654.

[6]張鐵.美式期權定價問題的數值方法[J].應用數學學報，2002，(1).

[7]約翰·赫爾.期權、期貨與衍生證券[M].北京：華夏出版社，1997.

[8]羅開位，候振挺，李致中.期權定價理論的產生和發展[J].系統工程，2000，(18).

[9]梁義娟，徐承龍.美式期權定價的數值方法[J].應用數學與計算數學學報，2013，(1).

[10]曹小龍，胡云姣.美式期權定價的擬蒙特卡羅模擬及其方差減小技術[J].北京化工大學學報：自然科學版，2014，(3).

[11]古麗麗，金朝嵩.美式看跌期權定價的控制變量法及其估值效率研究[J].經濟數學，2007，(4).

[12]馬俊海，劉鳳琴，張義珍.關于美式衍生證券定價的數值分析方法的分析與評述[J].管理工程學報，2000，(4).

[13]P.Wilmott，J.Dewynneand J.Howison.Option Pricing：Mathematical Modelsand Computation[M].Oxford Financial Press，Oxford，1993.