卡爾曼濾波在水下慣性導航系統中的研究及實現

雷曙光，張　柳，林列書

(廣州民航職業技術學院，廣東廣州510403)

卡爾曼濾波在水下慣性導航系統中的研究及實現

雷曙光，張柳，林列書

(廣州民航職業技術學院，廣東廣州510403)

摘要:首先建立慣性導航系統中的速度誤差、位置誤差、陀螺儀誤差模型，然后與現實相聯系研究帶偏移量的卡爾曼濾波，同時對偏移量進行估計，最后通過實驗驗證卡爾曼濾波對航向、陀螺儀誤差等的修正，極大地提高了水下慣性導航系統的結算能力和準確性。

關鍵詞:卡爾曼濾波;慣性導航系統;偏移量;估計量

The research and implementation of kalman filtering in INS integrated navigation

LEI Shu-guang，ZHANG Liu，LIN Lie-shu
(Guangzhou Civil Aviation College，Guangzhou 510403，China)

Abstract:First，this article established speed error，position error，gyro error model in inertial navigation system．Then linked with reality and researched on Kalman filter with offsets．At the same time estimated offset．Finally，experiments show that Kalman filter amendmented to the heading，gyroscope error，etc．This algorithm greatly improved the billing capability and accuracy of underwater inertial navigation system．

Key words:Kalman filter; INS integrated navigation; bias federated filter;estimator

0　引言

隨著科技的發展，利用導航對潛艇等非固定目標進行定位、定向等應用越來越廣泛，在復雜的海洋中對潛艇進行高精度的導航定位可以有效的預防意外事故的發生。慣性導航系統全天候都可以工作，隱蔽性強、帶寬寬，能夠平穩的提供才捕捉到數據信息。在狀態空間中卡爾曼濾波是典型的最優估計法。

本文首先建立了慣性導航系統中的速度誤差、位置誤差、陀螺儀誤差模型，然后與現實相聯系研究了帶偏移量的卡爾曼濾波，同時對偏移量進行估計，最后通過實驗驗證卡爾曼濾波在水下慣性導航系統中的作用。

1　建立慣性導航系統的數學誤差模型

在現實中船舶上的微機電系統在通電工作后，隨著時間的增長，元件自身的溫度會升高，同時環境、元件材質等影響使元器件的電壓處在一個動態變化的狀態，從而影響了慣性導航系統的精度，所以本文著重研究這種帶有偏置的卡爾曼濾波，在利用卡爾曼濾波之前應該獲取到慣性導航系統的數學誤差模型。

慣性導航系統的誤差有速度誤差、位置誤差、平臺誤差、陀螺儀和加速計等誤差［1－3］。

1)陀螺儀誤差方程

陀螺儀直接關系到慣性導航系統的姿態誤差。本文選用的陀螺偏移模型是AIC最小的AR(1)。

將AR(1)的數學表達式xk=φ1xk－1+αk轉換成連續的一階馬爾科夫x·(t) +βx(t) = z(t)，從而可以得到:

式中wg(t)為陀螺儀的隨機信號。

2)位置誤差模型

由

從而可以獲得空間直角坐標的位置誤差為:

3)航速誤差

根據慣性導航方程

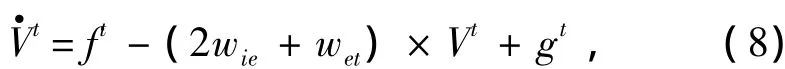
可知:

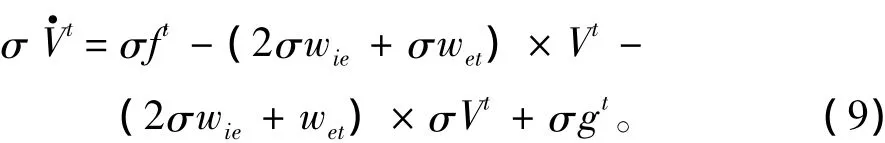
通常重力加速度被認為是常數，故σg= 0。令

則:

式中: fp為實際的加速度;Δp為測量的偏差。

則:

從而可得:

代入式(9)得到速度的誤差方程:

2　帶偏移量的卡爾曼濾波

參考文獻根據［4］可知，帶偏置的科爾曼濾波的估計狀態方程為:

觀測方程為:

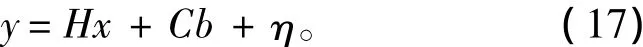
對式(16)和(17)進行離散可得:

式中: xn為第n個更新點變化向量; yn為第n個更新點的觀測向量; b為偏置向量; An，Bn，Hn，Cn均為隨時間變化的矩陣系數;ξn為系統數學期望為0時的噪聲;ηn為觀測噪聲。

在沒有偏置的理想情況下，得到的狀態方程為:

從而得到狀態的估計方程為:

式中: x為理想狀態下的估計; p為x的誤差協方差矩陣; kx為卡爾曼濾波的增益矩陣。

當偏置已知時，b就是固定值，則可以得到x的估計:

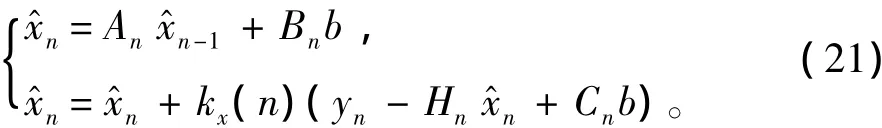
由式(20)和式(21)可得2個狀態的估計值關系為:

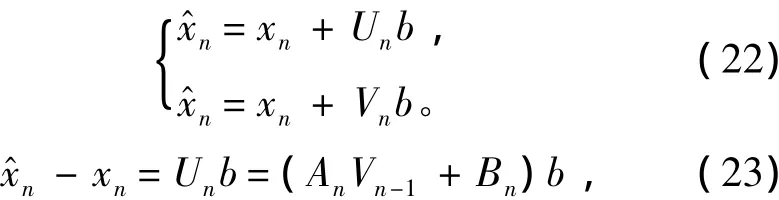
從而得到狀態的加權陣:

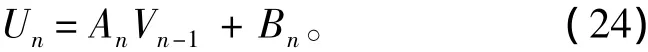
同時可知:

因此，可得關于每一步估計的狀態矩陣:

式中:

由式(24)～式(27)可以得到加權矩陣的類推方法。

沒有偏置情況下，濾波器的測量誤差為:

對上式作如下變換可得:

式中: vn為濾波估計的測量誤差，表述了與自估計偏移量之間的關系; vn不是一個固定的值，因此測量值與估計值沒有關系。

對偏移向量b進行估計:

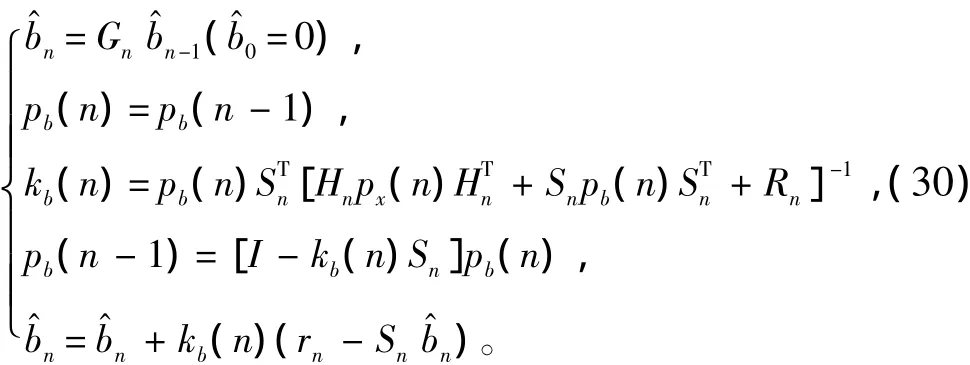
式中: px和rn根據沒有偏移量的情況估算求得; Sn通過式(24)～式(27)可得。

從而得到狀態估計的修正值，利用式(30)修正沒有偏移的x，從而得到最小方差估計表示為:

求偏移向量b的估計值

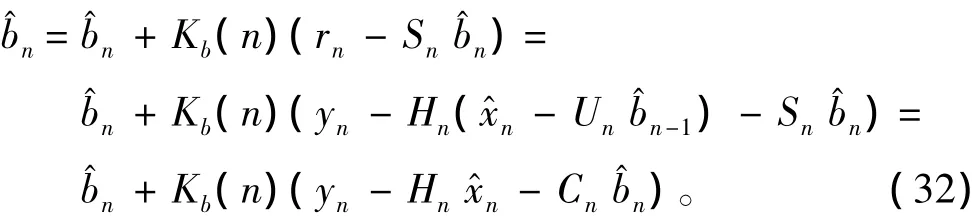
故而得到最小方差估計為:

通過以上推理可知卡爾曼濾波是利用兩部分之間的相互關系估算狀態偏差。步驟如下估算出在偏移量作用下的，同時可以求得協方差矩陣P，P有系統狀態X和b有關，根據二者影響的不同，可以將b對之的影響分離出來，從而求出偏移向量b。

3　帶偏移的卡爾曼濾波在慣性導航系統的應用實驗結果

本文通過建立六狀態下的卡爾曼濾波方程估算航行方向、陀螺儀角速度等的誤差。要估算的六狀態誤差為Δθ，Δγ，Δψ，Δwx，Δwy，Δwz。

由加速度計信號確定的姿態角θ0= 2.45°， γ0= 1.55°。令ψ0= 1°，從而獲得初始姿態矩陣，實驗結果如圖1所示(橫坐標表示時間，單位: s)。

圖1　六個狀態量的卡爾曼濾波誤差曲線Fig.1　Kalman filter error curve of six state quantity

從圖1可看出，航向角誤差和姿態角誤差在很短的時間內就接近于0，由此可知在經過卡爾曼濾波后，大大提升了系統的結算能力，并且準確度得以提高。角度的偏移量最大不超過±0.05°，一定時間后系統趨于平穩，從陀螺的角速度誤差曲線可以看到處于穩定的狀態。由此說明了帶偏移量的卡爾曼濾波通過偏移量修正改善了實際應用中因為偏移量所帶來的不準確性，提高了系統的穩定性。

4　結語

本文首先建立了慣性導航系統中的速度誤差、位置誤差、陀螺儀誤差模型，然后與現實相聯系研究了帶偏移量的卡爾曼濾波，同時對偏移量進行估計，最后通過實驗驗證了通過卡爾曼濾波對航向、陀螺儀誤差等的修正，極大提高了水下慣性導航系統的結算能力和準確性。

［1］LIU Hai-tao．Study and realization of the low-cost INS/GPS integrated navigation system algorithms［J］．Journal of Telemetry，Tracking and Command，2003，24(2) :36－41．

［2］WEN Wu．Federated filter of INS/GPS integrated navigation ［J］．Journal of North China Institute of Technology，2004，25 (4)．

［3］YAN Xian-gong．Research of kalman filter and its application in ship GPS/SINS integrated navigation［J］．Ship Science and Technology，2014，36(12) :128－131．

［4］BERNARD F．Treatment of bias in recursive filtering［C］/ / IEEE Transactions on Automatic Control，volAC－14，NO．4，AUGUST 1969:359－367．

作者簡介:雷曙光(1973－)，男，副教授，研究方向為飛機電子設備維修研究。

收稿日期:2014－10－26;修回日期: 2014－12－27

文章編號:1672－7649(2015) 07－0200－03doi:10.3404/j.issn.1672－7649.2015.07.047

中圖分類號:U665．26

文獻標識碼:A