群的判斷算法設計

姜 楠，張富彬，寧春芳

(大連民族大學 計算機科學與工程學院，遼寧大連116605)

群論是研究群的結構及其應用的數學理論，是代數系統的重要分支，它不僅在物理學、化學、力學、生物學中有著廣泛的應用，其應用范圍也深入到科學技術的各個領域［1－2］。尤其是在計算機科學領域的研究和應用中，群論已成為非常重要的工具。而且群論也是密碼學的重要理論基礎，例如組合群論中有些基本問題相對于某個特定的群是困難問題，可以作為構造公鑰密碼體制的基礎［3］，還有一些對稱加密算法和非對稱加密算法都是以群論為理論基礎的。群的理論比較抽象難以理解，本文設計了一個判斷群的仿真系統。首先設計了對代數系統進行判斷的算法，進而設計出判斷給定的代數系統是否為群的算法，最后通過Java 程序設計實現了群的判斷系統。

1 系統原理

代數，也稱代數結構或代數系統，是指定義有若干運算的集合。

定義1:非空集合S 和S 上k 個一元或二元運算f1，f2，…，fk組成的系統稱為一個代數系統，簡稱代數。記作＜S，f1，f2，…，fk＞［4］。

定義2:群 ＜G，* ＞是一個代數系統，其中二元運算* 滿足以下3 條:

(1)結合律，即對所有的a，b，c∈G，有

a * (b * c)=(a * b)* c (滿足結合律的代數系統為半群);

(2)含幺元，即存在一個元素e，對任意元素a∈G，有(含幺半群稱為獨異點);

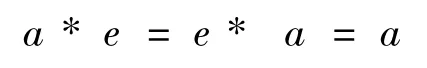
(3)存在逆元，即對每一個a ∈G，存在一個元素a–1∈G，使

a－1* a=a * a－1=e(稱G 為群);

簡單地說，群是一個具有可結合運算，存在幺元，每個元素存在逆元的代數系統［4］。

2 算法設計

2.1 代數系統的判斷

代數系統的判斷就是通過用戶自定義的集合和運算表，判斷給定的運算在相應的集合上是否封閉，如果封閉，則上述集合與運算構成代數系統，否則不能構成代數系統。判斷運算封閉的函數為judgeAlgebraicSystem()，對于給定的運算表，如果運算是封閉的，返回true，否則返回false。將給定的運算表中的元素和集合中的元素依次做對比驗證，如果運算表中的元素均屬于此集合，則此運算是封閉的。算法2.1 具體描述如下:

(1)給定n 個元素的List 類型的集合set，給定n 行n 列的List 類型的二維運算表operationTable，計數器count=0，運算表循環變量i=0，j=0，集合循環變量k=0;

(2)驗證運算表中所有的元素是否屬于該集合，依次取出運算表中第i 行第j 列元素，與集合set 中元素對比，通過語句operationTable. get(i).get(j). equals(set. get(k))進行判斷。如果存在相等，則計數器count + +，并且跳出k 層循環，j=j+1，i=i +1;否則k 層循環結束后j=j +1，i=i+1;

(3)直到循環結束將運算表中所有元素驗證完畢，執行(4)，否則執行(2)

(4)若count 的值與運算表中元素數量相等，則構成代數系統，返回true，否則不能構成代數系統，返回false。

2.2 判斷給定的代數系統是否為半群

在已知給定的系統是代數系統的基礎上，判斷此代數系統是否為半群的函數為judgeCombination()，根據結合律公式(a * b)* c=a* (b * c)設計算法，首先求出等式左側前兩個元素作用的值，然后取其值的下標，再與第三個元素進行運算，得出結果;然后求出等式右側后兩個元素作用的值，并取其值的下標，使第一個元素與之運算，得出結果，將兩次的結果進行比較如果相等返回true，如果不相等返回false。算法2.2 具體描述如下:

(1)給定n 個元素的List 類型的集合set，給定n 行n 列的List 類型的二維運算表operationTable，分別初始化代表三個元素的循環變量i=0，j=0，k=0;

(2)計算前兩個元素運算的結果operationTable.get(i). get(j)，暫存temp1 變量中，計算出temp1 的值在集合中的地址下標set. indexOf(temp1)，暫存add1 變量中;

(3)進入k 層循環，計算后兩個元素作用的結果operationTable.get(j). get(k)，暫存temp2 變量中，計算出temp2 的值在集合中的地址下標set.indexOf(temp2)，暫存add2 變量中，執行(4);

(4)驗證前兩個元素運算的結果temp1 與第三個值運算的值，同第一個元素與后兩個值運算的值temp2 運算的值是否相等，通過語句operationTable.get(add1). get(k). equals(operationTable.get(i).get(add2))進行判斷，如果兩次運算的值不相等，則代數系統不滿足結合律，返回false，結束程序;如果兩次運算的值相等，則k=k+1，j=j+1，i=i+1;

(5)直到所有循環運行結束，執行(6)，否則回到(2);

(6)代數系統滿足結合律，代數系統是半群，返回true。

2.3 判斷半群是否為含幺半群

在給定的代數系統是半群的基礎上，判斷其是否為含幺半群，這個判斷函數為judgeIE()，在半群中存在單位元則為含幺半群也稱為獨異點。對集合中任意元素a，如果有a* e=a，e* a=a，則此半群中存在單位元e。

算法2.3 具體描述如下:

(1)給定n 個元素List 類型的集合set，給定n 行n 列的List 類型的二維運算表operationTable，循環變量i=0;

(2)進入循環，計數器count=0，循環變量j=0;

(3)如果集合中第i 個的元素與第j 個元素運算的值等于第j 個元素，并且第j 個元素與第i個元素運算的值也等于第j 個元素，用語句operationTable. get(i). get(j). equals(set. get(j))＆＆operationTable. get(j). get(i). equals(set. get(j))進行判斷，如果成立count + +，j=j+1;

(4)如果j 層循環完畢，判斷count 的值是否等于集合的長度，如果相等，表明此時存在單位元，此半群是含幺半群，并且將單位元set. get(i)返回，程序結束;否則i=i+1;

(5)直到循環結束，執行(6)，否則回到(2);

(6)代數系統中不存在單位元，返回false。

2.4 判斷含幺半群是否為群

在給定的代數系統是含幺半群的基礎上，判斷其是否為群的函數是judgeInverseElement()，若在含幺半群中每一個元素都存在逆元，此含幺半群為群，對代數系統任意的a 存在a * a－1=e，a－1* a=e，a－1屬于集合set，則此元素存在逆元。算法2.4 具體描述如下:

(1)給定n 個元素List 類型的集合set，給定n 行n 列的List 類型的二維運算表operationTable與單位元ie，設置計數器count=0，循環變量i=0，j=0;

(2)利用運算表，依次取出運算表中第i 行j列元素，驗證集合中第i 個元素與第j 個元素運算的值，同第j 個元素與第i 個元素運算的值是否同時為單位元，通過語句operationTable. get(i).get(j). equals(ie)＆＆operationTable. get(j). get(i).equals(ie)判斷，如果所得的兩個值同時為單位元，則計數器count+ +，否則j=j+1，i=i+1;

(3)直到循環結束，執行(4)，否則回到(2);

(4)如果count 的值與集合長度相等，表明所有的元素均具有逆元，含幺半群是群，返回true，否則表明某個元素不存在逆元，含幺半群不是群，返回false。

3 系統實現流程

本系統是通過Java 語言編程實現的。對于一個非空集合G 以及定義在G 上的代數運算所構成的系統，判斷＜G，* ＞其是否為代數系統，首先需要給定集合set，以及定義在集合上的運算構成的運算表operationTable，通過類JudgeAlgebreic-System 聲明對象jas，調用函數judgeAlgebreicSystem(operationTable，set)，通過算法2.1 判斷運算是否封閉，如果返回true，則運算封閉，輸出“運算封閉，是代數系統”，程序繼續執行，如果返回false，運算不封閉，＜G，* ＞不是代數系統，輸出“不是代數系統”，程序結束。

在滿足代數系統的基礎上，通過類JudgeCombination 聲明對象jc，調用judgeCombination(operationTable，set)，通過算法2.2 判斷代數系統是否滿足結合律，如果程序返回true，則表明代數系統滿足結合律，此時代數系統是半群，輸出“運算可結合，此代數系統是半群”，否則返回false，代數系統不滿足結合律，輸出“運算不可結合，此代數系統不是半群”，程序結束。

在滿足半群的基礎上，通過類JudgeIE 聲明對象jie，調用judgeIE(operationTable，set)，通過算法2.3 判斷半群是否含有單位元，如果存在，函數將單位元返回用result 接收，并輸出“單位元，此代數系統是含幺半群”，否則返回false，輸出“此代數系統不存在單位元，不是含幺半群”，程序結束。

在滿足含幺半群的基礎上，通過類JudgeInverseElement 聲明對象jie2，調用judgeInverseElement(operationTable，set，result)，通過算法2.4 驗證是否每個元素均存在逆元，如果返回true，則表明所用元素均存在逆元，輸出“所用的元素均存在逆元，此代數系統是群”，否則返回false，輸出“部分元素不存在逆元，代數系統不是群”，程序結束。

系統實現流程圖如圖1 。

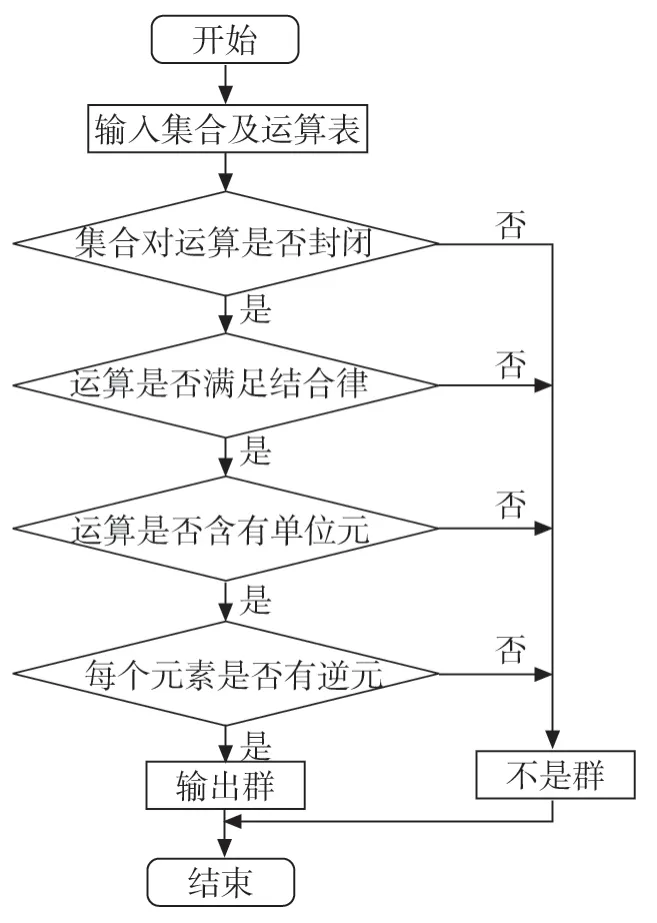
圖1 系統流程圖

4 結 論

群論是離散數學課程的重要組成部分，也是一種非常重要的代數系統，在很多領域都有應用，尤其是在計算機和通信以及信息安全領域有更為廣泛的應用。本文主要研究給定集合與運算是否構成代數系統、是否構成半群和獨異點，對給定的代數系統是否構成群的判斷系統的原理與算法設計，并且編程實現了群的判斷系統。該系統把抽象難以理解的代數中的群論問題通過形象直觀的程序軟件表現出來，不僅可以幫助學生更好的理解書本上學過的抽象的難以理解的代數系統理論，還可以提高學生的數學建模能力、算法分析設計能力和程序設計能力。既提高了學生各方面的能力，又培養了學生的學習興趣，可以很好的提高教學質量。

［1］李奴義.淺議群論在化學中的應用［J］.青海師范大學民族師范學院學報，2012，23(1):95 －96.

［2］何劼. 用群論的基礎知識理解信號處理中的一些基本概念［J］.中央民族大學學報(自然科學版)，2007，16(3):259 －261.

［3］湯學明，洪 帆，崔國華. 辮子群上的公鑰加密算法［J］.軟件學報，2007，18(3):722 －728.

［4］屈婉玲，耿素云，張立昂. 離散數學［M］. 北京:清華大學出版社，2014.