學習從哪里開始？

編者按

特級教師，可謂大家公認的“好老師”。一個學生、一個班級能有特級教師來任課，無疑是幸運的。本刊特設此專欄，將特級教師的“三尺講臺”設立在此，就是希望通過特級教師的講學，帶動廣大教師的專業提升，讓所有的學生、所有的班級，都能幸運地享受高水平的教學。

另外，各位讀者可就每期主講特級教師的講解內容開展討論。我刊《互動問答》專欄將刊出讀者的提問、討論等內容，以進一步開拓與大家的互動研討，支持大家的專業發展。

本期主講特級教師

俞正強，浙江省小學數學特級教師，北京師范大學教育家書院首屆兼職研究員，浙江師范大學碩士生導師，浙江省金華市環城小學校長。

平均數，在學生的數感發展中具有非常重要的地位。在學習平均數之前，學生所接觸的數都對應著物品，具有實在性，而平均數則既可能是一組數中現成存在的，也可能是一組數中不存在的。它反映的不是物的多少，而是一組數的整體水平。這種發展，對學生的數感成長而言，其意義是非常重要的。也因此，在小學數學界，我們一直將平均數的認識作為一節重要的課題，加以研究。

目前教材中，不論哪個版本，基本上會用以下的素材來開展平均數的學習：

問：兩個隊，哪個隊的水平比較高？或選哪個隊代表班級去比賽？

教材用這一材料或類似材料，是基于以下對學生關于比較的發展水平的認識：

第一：一對一比，比大小。如甲8個，乙6個。8>6

第二：多對等多比，比總數。如甲8個和7個，乙6個和9個。8﹢7=6﹢9

第三：多對不等多比，比平均數。比如前面書中的例題。

對這個過程的認識無疑是正確的。但有一個問題很致命，即在此一問題情境下，平均數是用來解決問題的。即軍隊若要打100千米以內的目標，可以用炮，但打1000千米的目標，則需要用導彈。但在用導彈之前，我們應該先有導彈，即武器庫內應儲存導彈才能用導彈，不可能在用導彈中制造出導彈。

也就是說，學生在用平均數來解決遇到的因人數不等而不能用總數解決的問題時，他們的知識儲備中應該已經有了平均數的認識。

為此，我在帶領學生學習平均數的認識時，先用了以下這份材料。

材料：

二年級小朋友丁丁，60米跑了5次，測得時間分別是：

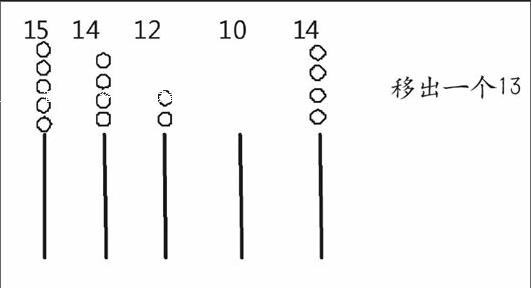
15秒 ? 14秒 ? 12秒 ? 10秒 ? 14秒

第二天他向老師匯報：

60米我要跑 ?15 ?秒

老師一問：丁丁為什么填了15秒，卻把15又劃去呢？

學生討論：15秒是他跑得最慢一次，他不甘心，就劃去了。

老師出示材料：60米我要跑 ?15 ?秒

10 ?秒

老師二問：丁丁填了10秒，又為什么劃去呢？

學生討論：10秒是他跑得最快的一次，他沒有把握一定跑出來，不好意思填10秒。

老師三問：對，寫15秒太慢不甘心，10秒太快不好意思寫，你覺得丁丁會填幾秒呢？

學生討論：12秒 偏快

14秒 偏慢

13秒 不快不慢

但沒有跑出來過

課堂討論進行至此，關于平均數的兩個理解要點已經出來了。

要點一：13秒表示水平正好，不慢不快。

這是學生支持的理由，說明他們完全理解平均數用來代表一組數整體水平的內涵了。

要點二：13秒，他從來沒有跑出來過，怎么能算呢？

這是學生反對的理由，說明他們尚未接納虛擬數。

由此，接下來的關鍵在于討論13秒，到底丁丁能不能填的問題了。

老師四問：13秒沒有跑出來過，那13秒怎么來的？

學生討論：①13秒在14和12的中間。

②13秒在15和10的中間。

這里已經有了平均數的算術意義上的理解了，它是最大數與最小數之間的中間數。

老師五問：13秒最能表示丁丁的一般水平，可是卻沒有跑出來過，能填嗎？

學生討論：也許第六次就能跑出13秒啊！

課堂進行到這里，小朋友都有此體會了。對啊，可以跑第六次啊！同學們開始接受13秒了，意味著學生們開始接受虛擬數了。

老師六問：同學們，那么13和15、14、12、10、14這組數間有內在聯系嗎？

學生討論：可以用移動法，移出一個“13”。

可以計算出一個“13”。

②（15+14+12+10+14）÷5=13

老師七問：剛才我們認識了平均數，那么平均數有什么用呢？能幫助我們解決什么問題呢？

接著采用教材中的例題繼續教學。

（責任編輯：林靜）