GNSS擬合高程代替三等水準測量的可行性分析

粟劍

(中鐵二局第二工程有限公司,成都 610073)

?

GNSS擬合高程代替三等水準測量的可行性分析

粟劍

(中鐵二局第二工程有限公司,成都 610073)

摘要：應用GNSS擬合高程時,需要根據已有數據分析其精度及可靠性．以某新建高速鐵路CPⅠ控制網和二等水準數據為基礎,在EGM2008地球重力場模型的基礎上,采用曲線擬合法將GNSS大地高轉換為正常高,計算每測段擬合高差與二等水準高差的差值,進行GNSS高程擬合精度評定．數據統計結果顯示,以二等水準高差為真值,該方法GNSS擬合高程可以達到三等水準的精度。

關鍵詞：GNSS;高程異常;EGM2008;曲線擬合

0引言

GNSS具有測量精度高、速度快、無需通視遠距離測量、操作簡單等優點,已經在平面控制測量領域得到了廣泛的應用。GNSS測量可以同時得到高精度的基于WGS-84橢球的大地高,而我國采用正常高系統,需要進行高程轉換。目前,GNSS高程擬合方法較多,常用的方法有采用數學模型擬合和基于地球重力場模型計算,數學模型包括多項式曲面擬合、多面函數擬合、神經網絡擬合等[1-4],常用的地球重力場包括EGM2008、EGM96等[5]。新建高速鐵路成都至貴陽線樂山至貴陽段某標全長約39 km,精測網包括CPⅠ、CPⅡ控制網、二等水準控制網等,每隔約4 km布設一對CPⅠ控制點。以現有數據為基礎,選擇合適的地球重力場模型和擬合方法,探討GNSS高程擬合精度,對于以后類似項目應用,具有一定的作用。

1已有數據分析

1.1GNSS數據

選用精度較高的CPⅠ控制網數據進行分析。CP I控制網采用雙頻接收機按二等GNSS控制網要求進行觀測,采用邊連接形成三角形或大地四邊形組成帶狀網。測量時每條邊觀測時段數≥2,PDOP值均≤6,有效時段長度≥90 min,GNSS接收機采樣間隔為15 s,衛星高度角≥15°[6].

CPⅠ控制網數據使用Pinnacle軟件進行基線向量解算,采用工程測量數據處理通用軟件GSP進行基線平差計算。經統計,CP I基線向量網閉合環閉合差,重復觀測基線長度較差,以及平差后的最弱邊方位角中誤差、最弱邊邊長相對中誤差、最弱點點位中誤差均能滿足《高速鐵路工程測量規范》的精度要求。

1.2二等水準數據

二等水準網采用徠卡DNA03精密電子水準儀及配套的3 m銦鋼條碼尺,按《國家一、二等水準測量規范》二等水準測量要求作業。

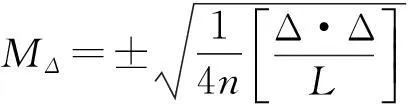
二等水準網的數據處理采用武漢大學科傻地面控制測量數據處理系統軟件按嚴密平差方法進行水準網整體平差。平差后最弱點高程中誤差為6.47 mm,可以滿足二等水準測量精度要求。

聯系人： 栗劍 E-mail: sj421814405@163.com

1.3數據綜合分析

綜上,已有數據CPⅠ控制網按照二等GNSS控制網要求布設,高程控制網采用二等水準方法測量,數據均滿足《高速鐵路工程測量規范》限差要求,精度較高,為GNSS高程擬合精度分析提供了良好的基礎。

2擬合方法及結果

2.1EGM2008地球重力場模型

EGM2008地球重力場模型是美國國家地理空間情報局歷經四年,充分利用最新數據,在多個國家和地區進行測試與評估的基礎上建立的新一代地球重力場模型[7]。EGM 2008地球型基本格網分辨率為5′×5′, 所采用的數據主要為衛星測高數據、地面重力數據、衛星重力數據等。截止目前,EGM2008地球重力場模型是分辨率最高、階次最多、精度最好的全球重力場模型[8]。

章傳銀、郭春喜、陳俊勇等利用Bruns公式計算GNSS/水準點的模型高程異常,并與GNSS/水準數據進行對比,對EGM2008地球重力場模型的適用性進行分析,結果如表1所示[8]。

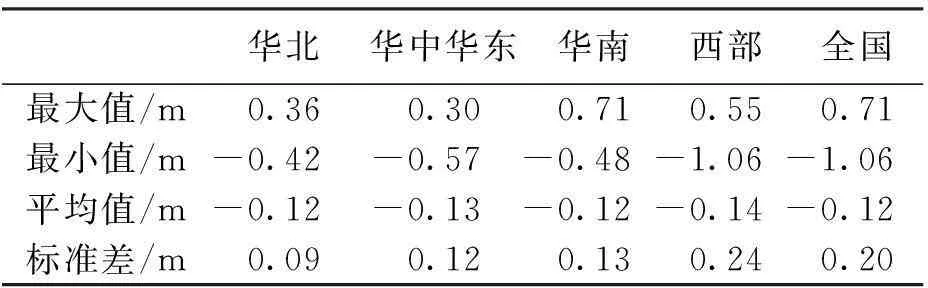
表1　EGM2008模型高程異常與GNSS/

2.2多項式曲線擬合

多項式曲線擬合模型適用于帶狀擬合。采取多項式曲線模型進行帶狀擬合時,將坐標系轉換為x與測線方向重合、y與測線方向垂直,設擬合點的高程異常ξi和擬合坐標xi的關系為

(1)

若式中只取a0、a1兩項時為直線擬合;當取a0、a1和a2三項時為二次曲線擬合,其中直線擬合必要觀測數為2個,二次曲線擬合必要觀測數為3個。計算時使用不同的GNSS/水準點數據,會得到不同的高程擬合結果,當GNSS/水準點數據較多時,需要采用逐步剔除法進行優化選擇。

2.3顧及EGM2008的GNSS高程擬合

2.3.1總體思路

GNSS高程擬合時,首先使用Bruns公式計算EGM2008模型高程異常,根據GNSS/水準高程異常計算EGM2008模型殘余高程異常(EGM2008模型高程異常與GNSS/水準高程異常的差值),采用二次曲線模型擬合EGM2008模型殘余高程異常,然后將GNSS大地高轉換為正常高。

2.3.2EGM2008模型高程異常計算

地球表面任意一點的模型高程異常可由Bruns公式計算得到:

Snmsinmλ)Pnm(sinφ),

(2)

式中:φ,λ,ρ為待求點的地心緯度、經度和向徑;γP為待求點的正常重力值; GM為引力常數與地球質量的乘積;a為參考橢球的長半軸; Pnm(sinφ)為完全規格化Legndra函數;Cnm、Snm為完全規格化位系數;N為模型展開的最高階數。

2.3.3EGM2008模型殘余高程異常計算

根據EGM2008模型異常及已知GNSS/水準高程異常計算EGM2008模型殘余高程異常:

ξ殘余=ξ模型-ξGNSS/水準

(3)

2.3.4基于二次曲線的殘余高程異常擬合

根據EGM2008模型殘余高程異常計算結果,將GNSS/水準點數據轉換為適合二次曲線擬合的數據,采用二次曲線法進行EGM2008模型殘余高程異常擬合,計算時,按照擬合殘差的分布情況,對已有數據逐步剔除,以保證擬合的精度。根據擬合結果求得待轉換點的EGM2008模型殘余高程異常,利用Bruns公式計算待求點的模型高程異常,從而將改點的大地高轉換為正常高。

2.4GNSS高程擬合結果分析

2.4.1GNSS高程擬合精度統計

根據高程擬合結果,計算相鄰CPⅠ擬合高程的高差,并與已有的二等水準測段高差進行比較,以二等水準高差為真值,計算擬合高差較差,精度統計結果如表2所示。

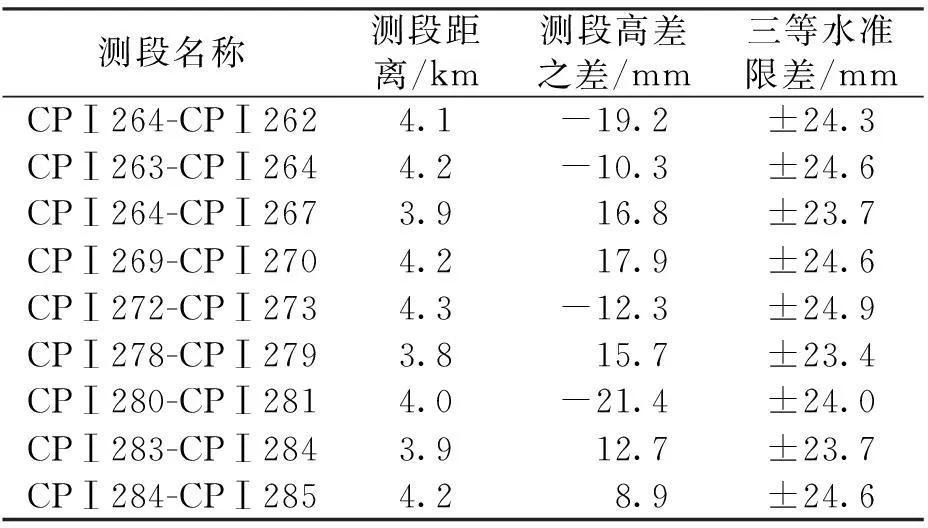
表2　GNSS高程擬合高差精度統計表

經過統計可以看出,基于EGM2008地球重力場模型的GNSS高程二次曲線擬合精度可以滿足三等水準的限差要求。將根據GNSS高程擬合結果計算得到的測段高差代替原水準網測段高差,并按照三等水準要求進行整網平差,水準網閉合差、平差后單位權中誤差均滿足三等水準的精度要求。

2.4.2原因分析

可以看出,GNSS高程擬合精度較高,經分析,主要有以下幾個原因:

1) 本次GNSS高程擬合采用的數據精度高,CPⅠ數據達到二等GNSS控制網要求,高程數據為二等水準精度,且測量時采用了強制對中觀測墩,最大限度的保證了基礎數據的準確性。

2) GNSS高程擬合時充分考慮了EGM2008地球重力場因素,采用二次曲線模型對EGM2008模型殘余高程異常進行擬合,提高了擬合的精度。

3) 本次擬合有足夠的GNSS/水準點數據,并采用逐步剔除法剔除了可能存在粗差的控制點數據,保證了GNSS高程擬合的準確性。

3結束語

以新建高速鐵路成都至貴陽線樂山至貴陽段某標CPⅠ控制網和二等水準數據為基礎,首先計算EGM2008模型高程異常,根據GNSS/水準高程異常計算EGM2008模型殘余高程異常,采用二次曲線模型擬合EGM2008模型殘余高程異常,然后將GNSS大地高轉換為正常高。將GNSS高程擬合結果與二等水準成果對比,經統計,擬合精度可以達到三等水準精度。該探討為以后類似項目GNSS高程擬合成果應用提供了很好的借鑒。

參考文獻

[1]朱春寧,王成,唐佑輝,等.GPS高程擬合模型選取及實驗分析[J].勘察科學技術,2014,(6):21-23.

[2]牛志宏.幾種基于神經網絡的GPS高程擬合方法比較[J].全球定位系統,2014, 39(2):64-67.

[3]徐平,杜向鋒.幾種常用似大地水準面插值方法精度分析[J].全球定位系統,2014, 39(2):79-81.

[4]林固記.二次曲面擬合GPS高程在臺山水庫灌區的應用[J].北京測繪,2014,(2):44-46.

[5]程懷遠.顧及EGM2008重力場模型的GPS高程擬合研究[J].全球定位系統,2014,39(1):82-84.

[6]劉凱,柳南鐵路CPⅠ變更測量分析[J].全球定位系統,2014, 39(1):76-78.

[7]蔡慶立,盧榮. EGM2008重力場模型在RTK高程測量中的應用[J]. 全球定位系統,2012,37(4):71-73.

[8]章傳銀,郭春喜,陳俊勇,等. EGM2008地球重力場模型在中國大陸適用性分析[J]. 測繪學報,2009,38(4):283-289.

粟劍(1980-),男,四川仁壽人,工程師,主要從事鐵路工程測量、施工測量工作。

Feasibility Analysis of GNSS Fitting Height

Substitute Third Leveling Surveying

SU Jian

(TheSecondEngineeringCo.,LtdofChinaRailwaySecondBoard,Chengdu610073,China)

Abstract:It is necessary to analyze the accuracy and reliability based on the existing data befor we use the GNSS fitting height. On the basis of a new high-speed rail network and the second level CPI control data and EGM2008 earth's gravitational field model,using curve fitting converted GNSS geodetic height to normal height, and calculated each test section and the second fitting height the difference between the standard height, height fitting accuracy assessment of GNSS. Statistics showed that in the second level elevation of true value, the method can make GNSS fitting height achieved third-level accuracy.

Key words:GNSS; abnormal height; EGM2008; curve fitting

作者簡介

收稿日期：2015-06-18

中圖分類號：P228.4

文獻標志碼：A

文章編號：1008-9268(2015)06-0092-03

doi:10.13442/j.gnss.1008-9268.2015.06.021