區域對流層模型在GPS高精度基線測量中的應用

孟祥伍

(吉林省地礦測繪院,長春 130062)

?

區域對流層模型在GPS高精度基線測量中的應用

孟祥伍

(吉林省地礦測繪院,長春 130062)

摘要：提出利用CORS網絡的觀測數據,基于PPP方法和多面函數擬合建立區域對流層模型,并利用該模型對GPS基線測量結果進行對流層延遲改正，通過實際GPS觀測數據計算對比發現,該方法能夠顯著提高GPS基線解算精度,優于傳統對流層改正模型。

關鍵詞：GPS基線;CORS;區域對流層模型;PPP

0引言

GPS信號穿過對流層時,由于大氣的折射作用,使得GPS信號的傳播路徑和傳播速度發生改變,因此產生GPS測量中的對流層延遲[1]。由于受氣象條件、測站位置等不同因素的影響,對流層延遲在天頂方向的值大約在1.9～2.5 m左右,在衛星高度角5°左右時甚至達到20 m,成為GPS測量中的重要誤差源之一[2]。大氣中干性成分和水汽成分造成的延遲分別稱為干延遲和濕延遲,其中干延遲可以利用經驗模型精確計算得到,而濕延遲難以利用傳統的經驗模型獲得較高精度的估值[3-4]。

常用的對流層模型主要用霍普菲爾德模型(Hopfiled)和薩斯塔莫寧模型(Saastamoinen)，然而由于對流層結構的復雜性和變化的快速性,對流層延遲受到大氣環境、測站地理位置、季節變化等多種因素影響,傳統的對流層模型難以滿足目前GPS測量精度要求[5]。本文提出利用PPP方法,基于GPS實測數據估計GPS測量時段的天頂對流層延遲,并利用多面函數模型對區域對流層延遲進行擬合,獲得測站的對流層延遲,進行高精度GPS解算[6]。

1區域對流層擬合模型

1.1PPP估計天頂對流層延遲

GPS單點定位中,線性化偽距觀測方程為

(Vion)i-(Vtrop)i,

(1)

線性化載波相位觀測方程為

λφi=-liVX-miVY-niVZ-cVtR-

(Vtrop)i+∑δi.

(2)

利用PPP方法估計對流層天頂延遲時,一般使用已知站點的觀測值,這樣可以消除坐標參數估計帶來的未知數,同時將精密衛星鐘差和精密星歷代入觀測方程[7]，利用雙頻觀測值消除電離層誤差的影響,則上述偽距和載波觀測方程轉化為

M(θi(i))-Pj(i)+εp,

(3)

M(θi(i))-λ·Nj(i)-

λ·Φi(i)+εp,

(4)

式中: j為衛星號; i為觀測歷元; c為真空中光速; δρzd(i)為對流層天頂方向延遲; M(θi(i))為投影函數; λ為GPS信號波長。根據以上觀測方程,構建未知參數的狀態方程,同時利用卡爾曼濾波等方法對參數進行解算,從而得到每個歷元的對流層延遲改正值。

聯系人： 孟祥伍E-mail:mxw25901294@163.com

1.2多面函數擬合模型

常用的對流層延遲擬合模型主要是二次或三次曲面模型,在估計對流層平面上的變化時只是建立了一個簡單的多項式模型,無法真實的反映對流層的精細變化。

多面函數的基本思想為:任意一個光滑的曲面總是可以用一系列規則的數學曲面以任意精度逼近表示。多面函數可表示為

(5)

式中: Q(x,y,xi,yi)為核函數; αi為模型參數; m為結點個數或顯著數據點個數，通常核函數為正雙曲函數或倒雙曲函數為

Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+

σ2]1/2,

(6)

Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+

σ2]-1/2,

(7)

式中: (xi,yi)為二次曲面的頂點; σ作為圓滑因子反映二次曲面在其頂點處的銳程度。利用PPP方法計算CORS網內多個基站的對流層延遲后,由于CORS基站較為密集,觀測質量高,觀測數據多,利用多面函數對對流層延遲進行擬合,能夠很好地反應對流層在平面上的相關性，另外考慮到對流層延遲受到測站高程的影響,需要對模型進行優化,增加代表高程的擬合參數為

bh+c.

(8)

2GPS測量實例分析

為了驗證該方法在GPS定位中的作用,選取一條長度約為2.4km的基線進行實際觀測和解算。接收機采樣頻率為30s,共觀測24h,每2h為一個時段,共劃分為12個時段。為保證解算的精度和準確性,首先與IGS站進行聯測,獲得該站的精確地心坐標,然后固定該站點對GPS基線進行解算。解算過程中分別采用霍普菲爾德模型、薩斯塔莫寧模型、區域對流層模型進行對流層改正,計算基線N、E、U三個分量和基線長度L.由于無法確定該基線的真值,因此根據基線重復率判斷基線測量的精度為

(9)

圖1是三種基線解算方案的基線重復率的對比圖。其中圓圈符號曲線為不加對流層改正模型的解算結果;星號曲線為hopfield模型對流層改正結果;正三角形曲線為通過區域對流層模型改正得到的基線解算結果。從圖中可以看出,無對流層改正模型的基線解算結果與其余兩種方案有較大偏差,并且不同時段基線解算結果變化較大,說明對流層延遲對基線精度影響較大，而hopfield模型改正結果與區域對流層模型改正結果相比,較為接近,但是不同時段的變化仍然比較大,區域對流層模型不同時段解算結果變化較小,基本在平均線周圍,說明區域對流層模型對GPS基線對流層延遲改正精度較高。

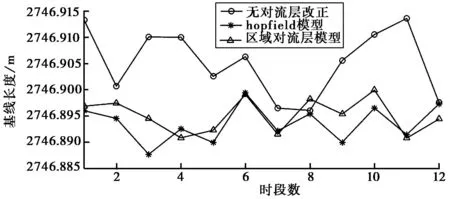
圖1　三種方案基線重復率對比

表1示出了三種方案獲得基線解算結果重復性精度統計結果。從表中可以看出,無對流層模型的基線解算質量相比于兩種改正模型精度相差加大，而hopfield模型改正精度中,基線重復率R為0.000 43 m,不同時段基線結果標準差STD較大,為0.003 5 m.區域對流層模型改正后的基線解算結果相比于傳統改正模型改正精度獲得了顯著提高,其中基線重復率R為0.000 32 m,不同時段基線結果標準差STD為0.002 8 m.說明該方法在實際中有應用前景。

表1　基線重復性精度統計/m

3結束語

對流層延遲對GPS測量精度影響較大,并且不能通過雙頻差分等手段完全消除，傳統的對流層經驗模型并不能滿足高精度GPS測量的精度要求。本文提出利用當地CORS網絡的觀測數據建立對流層模型,對GPS觀測結果進行對流層延遲改正。通過實際GPS基線測量項目的解算結果對比表明,區域對流層模型能夠對GPS基線測量結果進行較好的改進,使得基線精度相比與傳統對流層改正模型獲得了顯著提高。本文利用PPP方法計算對流層延遲需要IGS發布的事后精密星歷、精密鐘差等數據,不能做到實時建模,在實際工程應用中有一定的限制,利用預報星歷、快速星歷等數據進行該方法的計算精度需要進一步實驗的驗證。

參考文獻

[1]熊永良, 黃丁發, 丁曉利,等. 基于多個GPS基準站的對流層延遲改正模型研究[J]. 工程勘察, 2005, (5):55-57.

[2]張笑凡, 何宏, 陳建峰. GPS技術中對流層延遲影響分析[J]. 測繪與空間地理信息, 2014, (2):187-188.

[3]張婷婷, 徐子喬, 董思學. GPS天頂對流層延遲計算方法研究[J]. 全球定位系統, 2013, 38(1):22-27.

[4]錢闖, 何暢勇, 劉暉. 基于球冠諧分析的區域精密對流層建模[J]. 測繪學報, 2014, 43(3):248-256.

[5]陳招華, 匡翠林, 蔡昌盛. 區域精密對流層延遲建模[J]. 武漢大學學報·信息科學版, 2011, 36(4):392-396.

[6]趙鐵成, 韓曜旭. GPS定位系統中幾種對流層模型的探討[J]. 全球定位系統, 2011, 36(1):46-52.

[7]李凱鋒, 歐陽永忠, 任來平,等. GPS精密單點定位中對流層延遲處理方法研究[J]. 測繪科學, 2009, 34(4):93-94.

孟祥伍(1972-),男,吉林長春人,工程師,主要從事測繪工程相關工作。

Application of Regional Tropospheric Model in GPS High

Precision Baseline Measurement

MENG Xiangwu

(JilinInstituteofGeologyandMineralResourcesSurveyingandMapping,

Changchun130062,China)

Abstract:The observation data of CORS network is put forward, and the model is built based on PPP method and multi surface function fitting. The model is used to correct the GPS baseline measurement. By comparing with the actual GPS data, it is found that the proposed method can significantly improve the accuracy of the baseline solution of GPS, and which has great advantages compared with the traditional troposphere correction model.

Key words:GPS baseline; CORS; regional tropospheric model; PPP

作者簡介

收稿日期：2015-08-27

中圖分類號：P228.4

文獻標志碼：A

文章編號：1008-9268(2015)06-0049-03

doi:10.13442/j.gnss.1008-9268.2015.06.010