平面度誤差評定的幾種方法

□吳呼玲

目前，對平面度誤差評定常用的方法有:對角線法，任意三點法，最小包容區域法三種。對角線法是學生在平面度誤差檢測中常用的方法;最小包容區域法是課堂上教師講授的主要評定平面度的方法;任意三點法是不常用的方法。在實際的教學中，課堂的理論教學與實際評定的方法不吻合。本文提出幾種不同的平面度誤差處理方法，以及處理結果。

一、平面度誤差的評定方法

(一)對角線法評定平面度誤差。對角線法評定平面度誤差的判斷依據就是將被檢測的物質表面的一條對角線作為被測表面，并且將與另一條對角線平行的作為評定的基準面，這樣就會得出對平面度誤差值的確定，即以平行基準面其距離最小的平面間距離。

(二)三遠點法評定平面度誤差。三遠點法:是以通過實際被測表面上相距最遠，而且這些評定基面都不能在一條直線上，這樣一來平行與基面，并且距離最小的平面間就是平面度誤差值。

(三)最小區域法評定平面度誤差［1］。最小區域法就是以實際被測表面區域的寬度作為誤差值，該方法是目前應用比較廣泛的一種方法。

1．三角形準則。由兩平行平面包容被測面時，兩平行平面與被測面接觸點分別為3個等值最高(低)點與1個最低(高)點，且最低(高)點的投影落在由3個等值最高(低)點所組成的三角形之內，如圖1所示。

圖1 三角形準則

2．交叉準則。由兩平行平面包容被測面時，兩平行平面與被測面接觸點分別為兩個等值最高點與兩個等值最低點，且最高點連線的投影與最低點連線相互交叉，如圖2所示。

圖2 交叉準則

圖3 直線準則

3．直線準則。由兩平行平面包容被測面時，兩平行平面與被測面接觸點分別為兩個等值最高(低)點與一個最低(高)點，且一個最低(高)點的投影位于兩等值最高(低)點的連線上，如圖3所示。

二、三種方法評定平面度誤差的數據處理方法

在某基準平面上，用千分表測量一塊400(mm)×400(mm)平板的平面度誤差，測得數據如圖所示，求出其平面度誤差。

平面度誤差評定方法的數據處理采用旋轉變換理論［2］，如表1所示。

表1 旋轉變換理論

(一)用對角線法評定平面度誤差時的數據處理。對角線法評定平面度誤差的方法是，將通過被測平面的一條對角線且平行另一條對角線作為基準平面，以此基準面為基準，平面度誤差為被測實際表面偏離基準平面的最大偏離量，如表1所示，即公式(1):

求解得:P= -6;Q=2

求解得:p= -5;Q= -1

求解得:p= +2;Q= +5

將實際被測表面旋轉到與基準平面平行后，各點測得數據如表2所示。以包容被測平面上0～0對角線，且平行于(-6)～(-6)對角線作為基準平面，實際被測表面偏離基準平面的最大值為+16，最小值為-19。因此，該平面的平面度誤差為實際被測表面偏離基準平面的最大值與最小值之差，即+16 -(-19)=35μm。

(二)三遠點法評定平面度誤差時的數據處理。三遠點法是在被測平面上選取最遠且不在同一直線上的三點作為基準平面，以此基準面為基準，平面度誤差為被測實際表面偏離基準平面的最大偏離量。如表1 可見，即公式(2)。

表2 對角線法各測點數據圖

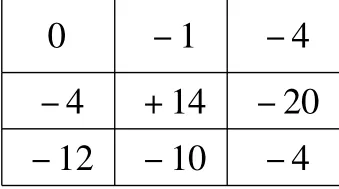
表3 三遠點法各測點數據圖

表4 最小區域法各測點數據

將實際被測表面旋轉到與基準平面平行后，各點測得數據如表3所示。以-4，-4，-4 三點作為基準平面，實際被測表面偏離基準平面的最大值為+14，最小值為-20。因此，該平面的平面度誤差為實際被測表面偏離基準平面的最大值與最小值之差，即+14 -(-20)=34μm。

(三)最小區域法評定平面度誤差時的數據處理。最小包容區域法是仔細觀察所測數據的分布情況，分析數據分布符合最小區域法中的三角形準則、交叉準則和直線準則中的哪一種。然后選擇基準平面，平面度誤差為被測實際表面偏離基準平面的最大偏離量。如表3所示，該測量數據符合三角形準則，其中+20 為最高點，-10，-9 和0 為最低點，組成三個低點形成的三角形中包容一個高點的情況。如表1 可見，即公式(3)。

將實際被測表面旋轉到與基準平面平行后，各點測得數據如表4所示。以0，0，0 三點作為基準平面，實際被測表面偏離基準平面的最大值為+20，最小值為0。因此，該平面的平面度誤差為實際被測表面偏離基準平面的最大值與最小值之差，即+20 -0 =20μm。

三、三種方法評定平面度誤差時的數據處理結果比較

三種方法評定平面度誤差的數據處理結果顯示，課堂理論教學中所講的最小包容區域法與實驗操作中所用到的對角線法測量平面度誤差的結果有所偏差。在教學中應該注意理論教學與實踐教學的統一性，告知學生平面度誤差的評定應該根據被測產品的實際情況選擇相應的方法。

［1］傅成昌．形位公差應用技術問答［M］．北京:機械工業出版社，2009:310～311

［2］林景凡． 旋轉變換理論及其在平面度誤差評定中的應用［J］．齊齊哈爾大學學報，2003，19 (3):75～76

［3］羅夢文．平面度誤差測量及數據處理研究［J］． 裝備制造技術，2011，1:96～97

［4］朱慶科，李成貴．平面度誤差測量的幾種方法［J］．計量與測試技術，2000，8:8～9

［5］雷賢卿，李飛，涂鮮萍，王世鋒．評定平面度誤差的幾何搜索逼近算法［J］．光學精密工程，2013，5

［6］鄭凱，金路．基于PC-DMIS 軟件的平面度誤差評定方法的分析［J］．黑龍江科技信息，2015，5