小學數學練習課教學實踐與思考

陳慶憲

小學數學教學中的主要課型有新授課、練習課和復習課，其中練習課約占總課時數的55%，所以提高練習課的教學效率是確保教學質量的重要途徑之一。練習課的重要性在教師心中應該是很清楚的，但為什么一直以來許多老師對練習課的教學感到困惑，談起它的設計就沒有一定的章法呢？分析其原因，我覺得主要有以下幾方面：一是練習課的教學內容不像新授課那樣清晰而充實，練習課的教學流程又不像復習課那樣在明確的梳理中提升。二是練習課作為新授課的延續，往往會碰到教材提供的練習量比較少，需要教師在量上作一些補充，或者對練習形式進行適當改變。三是部分教師認為練習課就是給學生練練、講講，顯示不出課堂中的“精彩”。有這樣想法的老師在教學上往往只關注自己如何“教”，沒有很好地考慮學生如何“學”。之所以存在這些原因，在于平常的教研活動中針對練習課的研究不是很多，長此以往對它的研究也就相對比較薄弱了。如何上好練習課，尤其在新課程背景下怎樣提高練習課的教學效率？這一問題值得我們深入思考。本文就從練習課的目標制訂、練習課的教學模式、練習課的練習設計等方面提出一些想法供大家研究時參考。

一、 認清課型定位，制訂教學目標

練習課是指新授課后教師有目的、有計劃地引導學生運用學過的知識進行一系列訓練、鞏固的教學活動。這種活動是圍繞著以訓練為主線、以思維為核心而展開的，是新授課的補充、延續和拓展。它的教學目的在于引導學生練習的過程中鞏固、提升、發展，在練習課的教學中要注意“練為主線、先練后評、分層交流、練中出新”。我們知道：一個知識與技能的獲得要經過實踐到認識，再由認識到實踐的過程，它需要學生通過幾次反復，在反復的過程中深化認知。只有這樣才有可能使學生的知識技能得到進一步熟練，思維能力得到進一步提高。這也說明教師要通過練習課教學為學生創設多次反復的機會，給學生提供及時鞏固和進一步深化的時間。

認清練習課的課型特點才能更好地制訂教學目標，那么怎樣制訂練習課的教學目標呢？我覺得可從以下兩個層面進行思考。

1.對練習課的總體目標進行思考

練習課的總體目標應該與《數學課程標準》提出的總目標一致，再針對練習課的功能特點提出以下四條：

（1）使學生進一步掌握課標提出的“四基”要求（基礎知識、基本技能、基本思想、基本活動經驗）。

（2）進一步發展課標提出的“四能”要求（發現和提出問題的能力、分析和解決問題的能力），進一步建立良好的智能結構。

（3）使學生進一步溝通知識間的聯系，掌握解決問題的策略與方法。

（4） 通過練習及時檢測、評價，進一步提高學生的學習興趣，增強學好數學的信心和養成良好的學習習慣。

2.對練習課課時目標的思考

課時目標是逐步走向總體目標的階段性要求，它是在落實新授課教學目標基礎上作適當提升而制訂的。在制訂課時目標時一定要考慮目標的整體性、層次性、發展性和可行性。所謂目標的整體性就是要在整體視角下制訂目標，做到心中既要有某一知識的總目標，又能夠針對一節課的側重點來制訂課時目標。對于目標的層次性，就是課時與課時之間的目標要具有一定的層次。我們知道練習課可以分為鞏固型練習課、綜合型練習課和發展型練習課。比如在“長方形、正方形的面積計算”新課教學結束后，我們可以按這三種課型來制訂練習課的教學目標。

第一節為“鞏固型練習課”。在這節課中我制訂的目標是：①在進一步掌握長方形、正方形面積計算方法的同時，能針對已知長方形的面積和長（或寬）的長度，計算它的寬（或長）的長度。②能熟練地解決實際問題中有關長方形和正方形的面積計算問題。

第二節為“綜合型練習課”。在這節課中，我制訂的目標是：①讓學生在練習中感受到周長的變化及其與面積的關系，知道當周長相等時正方形的面積要比長方形的面積大，或者面積相等時正方形的周長是最短的。②能計算由長方形和正方形簡單組合而成的圖形的周長和面積。

第三節為“發展型練習課”。在這節課中，我制訂的目標是：①使學生理解通過長方形或正方形邊的長度變化，而引起的面積的變化和周長的變化，進一步感知周長與面積的關系。②在圖形的觀察思考、畫圖和計算中進一步提高分析能力和空間想象能力。制訂這節課的教學目標時的思考與前兩節課有所不同，前兩節課是緊扣教材的練習內容來制訂教學目標，而本課是根據學生的實際情況和專項訓練的素材特意增加的專項訓練課，重在進一步拓展學生的思維。

由此，針對長方形和正方形面積教學后的三節練習課，充分體現了課時與課時之間的層次性和發展性。

二、突出練為主線，把握教學流程

教學流程又稱教學結構，它是教學方法具體實施的過程。當某種教學流程在長期采用的過程中逐步適應，這種課型的特點時，通常就成為這種課型的教學模式。但教學流程不一定都是高效的，而高效的教學流程一定是為完成既定的教學目標，在充分體現“以生為本”的教學思想基礎上，合理安排“教”與“學”的時間;高效教學流程也一定具有整體性、針對性、簡約性和可操作性，有利于教師把握和運用。我們知道練習課的主要教學策略是以練為主線，讓學生先練后組織評價。我們在這樣的教學思想引領下對不同類型的練習課進行實踐研究，逐步形成了比較穩定的教學流程，把它可分為以下四個層次：基本練習、專項練習、綜合練習和拓展練習。下面就以人教版教材三年級上學期《解決生活中的有余數除法問題》（以下簡稱“有余數的除法問題”）的練習課為例，談談對這四個層次練習的側重點和教學時間的大致分布情況。

1.基本練習

基本練習作為一節課的開始，它是針對本課練習重點設計的基本題，目的是讓學生練習后知道本課要練習的主要內容是什么，因此練習的量不宜過多，時間安排一般為2～3分鐘。

2.專項練習

專項練習一般是本節練習課的重點環節。在這一環節中要突出本節課主要的訓練點，所以在專項練習的內容設計上要“精”，時間安排一般為15～20分鐘。

3.綜合練習

綜合練習一般要在知識與技能上作出聯系與整合，進一步提升思維訓練的度，設計的練習內容要有一定的靈活性，時間安排一般為10～15分鐘。

4.拓展練習

拓展練習的設計是根據教學內容對知識作適當的拓展，在思維能力方面進行適當的提升，因此拓展練習的設計要把好一定的深度和發展度，時間安排一般為5分鐘左右。

在這里要提醒大家注意的是，以上四步教學流程適合大多數的練習課，對于特殊的內容可以作些調整，尤其對于綜合練習與拓展練習，有時也不一定分得特別清楚，只要以練為主線，恰當地把握好練習層次就可以了。

三、針對內容特點，精心設計練習

提高練習課教學效率的關鍵，是要給學生創設高效的練習素材。怎樣設計高效的練習，我覺得主要是針對一節課的教學目標和內容特點，在原有的練習基礎上進行創新性的整合、聯系、補充、改編和拓展。下面針對這幾方面的設計策略談談我的一些思考。

1.抓住知識技能的聯系，整合練習

在平常的課堂觀察中發現教師基本上能做到針對不同內容設計練習，可是見得最多的是每一道練習功能單一，教師沒有進一步去思考怎樣把相關的知識或技能整合在一起。因此出現了在一節課中練習的量雖然多，但效果不佳的現象。我認為教師善于針對內容特點和教學重點，把相關知識和技能進行合理整合是非常重要的。通過合理整合達到以少勝多，使學生在練中進一步引發思考。

2.注意上下環節的溝通，創設練習

在實踐中我們還發現，部分教師在設計練習時只注意到練習的層次性，而沒有很好地關注每一層次之間的溝通。出現環節與環節之間的練習形式和練習難度變化較大，不能很好地通過練習素材來進一步激發學生的練習興趣，總覺得課堂教學環節過渡不和諧、整體性不強。實際上在設計時注意上下環節練習的溝通，也是提高練習課教學效率很重要的策略之一。

比如，在教學“兩位數乘兩位數”的練習課中，我們設計了以下幾步練習：

第一步：不用筆算判斷下面各算式計算結果是否正確。

①42×63=2306 ②23×74=1701

③59×38=15172 ④24×63=1512

學生經過獨立思考、交流評講后，明確了怎樣用估算的方法來評定。第①題十位上的兩個數相乘的積是“2400”，所以這一算式的計算結果應該大于2400。第②題個位不會是“1”。第③題的積不可能是五位數。第④題一時很難看出結果是否正確，教師就讓學生寫出豎式算一算。當學生知道第④題的積正確后，教師隨機引出下面的第二步。

第二步：教師向學生提出：最后一個算式“24×63=1512”在以下情境中解決的是什么問題？

當學生看出算式“24×63=1512”解決了王老師一共要付多少錢的問題后，教師又提出：你還能解答張老師的問題嗎？請你列出算式計算。

當學生列出算式“42×36”，計算后發現結果也是“1512”，教師有意把以上兩算式上下抄在一起讓學生觀察。學生發現以上兩個乘法算式，在一個算式里把每一個乘數十位上的數字與個位上的數字調換位置后剛好是另一個算式，這兩個乘法算式的積又是相等的。學生產生好奇，這時教師趁機引出下一步的練習。

第三步：教師提出，是不是真的都會相等呢？請你自己寫出其他的一個“兩位數乘兩位數”，先算出它的積，再把這個算式每一個乘數十位上的數字與個位上的數字調換后，組成另一個“兩位數乘兩位數”，再算一算是否真的積是相等的。

這時學生積極性高漲，自編自算后發現積不一定相等。

緊接著教師又提出：那好吧！積不一定相等，下面老師也寫了幾個，你們再算一算。

① 82×14和28×41 ②62×39和26×93

學生計算后發現又是相等的。這時教師又提出：這些相等的算式有什么規律嗎？

學生的思維再一次被激發，發現只要兩個數個位上的數字相乘與兩個十位上的數字相乘的積是相等的，這樣的兩位數乘兩位數把每一個乘數的十位數字與個位數字調換再相乘，它們的積一定相等。（考慮三年級的學生對于算理的理解可能有一定難度，我們就做了這樣的解釋，至于為什么留給學生以后思考。）

顯然以上練習過程環環相扣，學生的思維積極性得到了充分調動。之所以達到如此效果，關鍵是教師敏銳地抓住了數值的特點與規律，并利用這些特點與規律把練習的上下環節串聯在一起了，學生在這樣的自然引導下自覺地投入練習過程之中。

3.分析教材練習的要求，改編練習

我們知道教材是教學的依據，當然練習課也是如此。因為大多數練習課都是針對教材中的練習要求進行設計的，所以我在這里要提醒注意的是針對教材的練習不能局限于簡單的補充，重要的是教師要善于針對原有的練習素材作出創新性的改編和拓展。

比如，我們針對人教版數學五年級下學期（第130、131頁）的三個大題，設計一節“復式折線統計圖”練習課時，進行了以下改編和拓展。

教材中有一題要求學生根據某商場12個月每個月A、B兩種彩電的銷售量畫出復式折線統計圖，再針對統計圖進行分析。畫出12個月兩種彩電每月銷售量勢必要用去很多時間，而且這樣的畫圖又是重復操作。所以我先呈現前3個月的兩種彩電銷售量，讓學生只畫出這3個月的復式折線統計圖。我覺得畫3個月與畫12個月都能組織評講畫圖的要領，當學生畫圖、評講結束后，再利用投影呈現全年的折線統計圖并進行解讀，這樣就大大節省了教學時間。

教材上另一題說的是：某校五年級男、女同學在五一期間不同度假方式的統計表，還有某校男、女同學在五一期間參加旅游人數的統計表。要求學生根據這兩張表所統計的內容是選擇畫復式條形統計圖，還是選擇畫復式折線統計圖。我覺得用這兩組統計數據來區分哪一組應該選用哪一種統計圖，其意義并不大。于是我們將此題改換成一張反映四個商場某月甲、乙兩種商品銷售量的表，另一張表是某一個商場在四個月中每個月甲、乙兩種商品的銷售量。學生根據這兩張表所反映的內容和數據去選擇應該畫成哪一種統計圖比較合適，這樣所產生的對比效果就截然不同了。

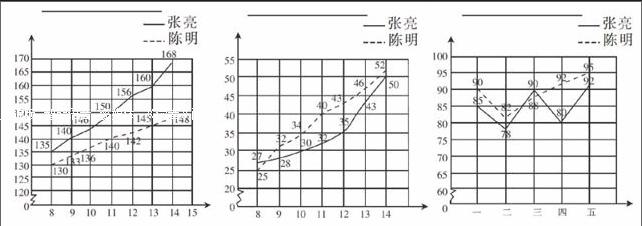
教材中還有一題是提供了陳明同學從8歲到14歲每年生日時測量的體重與標準體重比較的復式折線統計圖。此題只要求學生看懂這樣的復式折線統計圖，我覺得思維價值不高，因此，我借此題的素材作了拓展性的設計，把它改編成如圖所示的三組復式折線統計圖，要求學生根據圖中的數據特點展開想象，每幅圖表示的是張亮與陳明兩位同學的什么情況，請你給統計圖補充完整。

學生通過對這三幅圖數據特點的分析，從中看出第一幅圖表示的是張亮和陳明同學8～14歲的身高統計圖;第二幅圖表示的是張亮和陳明同學8～14歲的體重統計圖;第三幅圖表示張亮和陳明同學五次考試成績的統計圖。學生在解讀圖的同時對圖重新補上標題，以及縱坐標和橫坐標所表示的意思。接著教師又借助投影在第一張圖上呈現8～14歲兒童標準身高的折線;在第二張圖上呈現8～14歲兒童標準體重的折線;在第三張圖上呈現這五次考試全體同學平均成績的折線。再次引發學生觀察這三幅圖，分別說一說張亮和陳明同學與標準身高、標準體重、班級平均分的比較會是怎樣的。

由此可見，這節課的練習設計是從分析原教材練習素材入手，在把握原有練習要求的基礎上進行了呈現方式的改進，或對內容進行了合理的改編和拓展。我覺得這樣的改編和拓展會給學生帶來更有價值的思考，這也是練習設計的重要策略之一。

當然，對于練習課的練習設計的策略還有很多值得我們思考，比如根據教學內容和學生實際去尋找專題訓練素材設計練習課，在這種專項性的練習課中練習設計又會更加靈活，更有獨到之處。總之，練習設計要根據教學目標和內容特點，在關注學生主動參與、關注學生思維價值的前提下，由淺入深地設計練習素材，才能更好地提高練習課的教學效率。？筻