淺析發散思維的培養
劉小寶
思維被譽為地球上最美麗的花朵,被認為是人的心靈的中樞。根據思維過程中的指向性不同,可將思維分為集思維和發散思維兩種,它們都是學習思維組成部分。
發散思維是指思考問題信息朝各種可能的方向擴散,并引出更多的新信息,是思考者能從各種設想出發,不拘泥于一個途徑,不局限于既定的理解,盡可能多的作出合乎條件的解答。
從當前的初中物理教學發現,大多數學生的發散思維能力不足,致使一些同學學習物理有障礙,為此在教學中應根據初中物理教材內容、特點與學生思維發展特點加強思維能力的培養。
發散思維包含橫向思維、逆向思維及多向思維。發散思維具有多向性、變通性、流暢性、獨特性的特點,即思考問題時注重多思路、多方案,解決問題時注重多途徑、多方式。它對同一個問題從不同的側面、不同方向、不同層次橫向擴展逆向深入,采用探索、轉化、遷移、變換、構造、變形、組合、分解等手法,開啟學生心扉,激發學生潛能,提高學生素質,對造就創造性入才至關重要。那么,如何培養學生的發散思維能力呢?
一、訓練學生對同一條件聯想到多種結論的發散思維習慣
這種思維習慣是指確定了已知條件后沒有固定的結論。讓學生自己盡可能多的確定未知結論,并去求解這些未知結論,這種過程充分揭示思維的廣度和深度。不同層次的學生都能得到有益的嘗試。
圖(1)
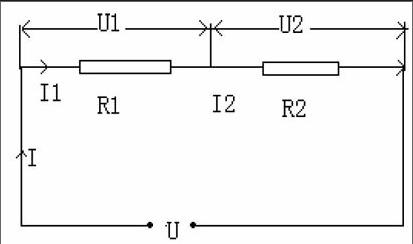
例如:如圖(1)所示,兩電阻串聯,R1=6歐姆,R2=9歐姆,把它們接在9伏的電路中,能求出哪些物理量?
分析:根據串聯電路的特點:
I=I1=I2 (1)
U=U1+U2 (2)
R=R1+R2 (3)
P=P1+P2 (4)
可從上述公式網中看出共有十個量,豎向I、U、R、P只要知道四個量中的兩個量可求出另外兩個量,橫向(2)、(3)、(4)式中知道兩個量可求出第三個量。所以,在此公式網中,若已知三個量R1、R2、U,則其他七個量可以全部求出,并由此擴展,只要知道公式網中的三個物理量(不是同行、同排的三個量),則其他七個量可全部求出。
二、訓練學生一題多變,通過擴展、延伸,達到做一題會一片的效果
這種思維習慣是指問題確定后,盡可能聯想與之相關的知識點,多設問、引導啟發學生對此題擴展延伸。
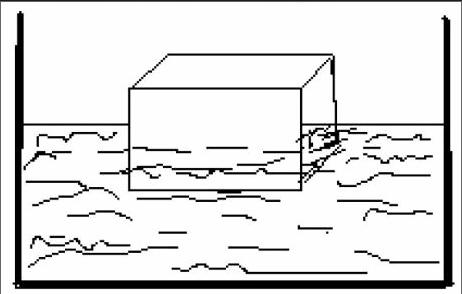
例2:如圖(2)所示,浮在水面上的木塊,它沒入水中的體積是50立方厘米,它在水面上部分的體積是25立方厘米,問它受到的浮力是多大?它的質量是多大?它的密度是多大?
圖(2)
做完此題后,可由淺入深的拓展:
提問變化(一):將木塊露出部分截去,剩下的部分是上浮還是下沉?若在豎直方向分成兩半,情況又將如何?
解析:將木塊露出水面部分截去,根據物體的沉浮條件,由于F浮大于G,故木塊剩下的部分將上浮。若在豎直方向分成兩半時,根據浮沉條件,因為F浮等于G,故此兩部分既不上浮也不下沉。
提問變化(二):若將此木塊放在另一液體中,有四分之一的體積露出液面,問這種液體的密度是多少?
解析:因為F浮等于G,ρ液g V排=ρ木g V ,所以ρ液g 3/4 V=ρ木g V,ρ液=3/4 ρ木= 0.87×103 ㎏/m3 。
提問變化(三):若在此木塊上放一鐵塊能使木塊沒入水中,問所加鐵塊的重力是多少?
解析:木塊沒入水中時鐵塊的重力和木塊重力的合力與木塊所受浮力為一對平衡力,即:G鐵+G木=F浮,G鐵=F浮-G木。
提問變化(四):若在此木塊下懸掛一鐵塊,恰好能使木塊沒入水中,問所掛鐵塊的重力是多少?
解析:根據平衡條件可知,增加的浮力等于增加的重力,先求出V鐵,在求出G鐵。
三、拓展集中思維,訓練學生一題多解
這種思維習慣是指當運用集中思維尋求答案時,盡量向各個方向、各種角度拓展,以形成不同的思維鏈,并把這些思維鏈的異同加以比較、總結,以培養發散思維。
例3:體積是2×10-3m3 的銅球,測得其質量是8.9千克,試判斷該銅球是空心還是實心?
針對此題,可以采用三種方法解題,即“比較密度法”、“比較質量法”、“比較體積法”,雖然此題并不難,但學生往往不加思考,隨便選擇一種方法解答,教師應該指導學生加以比較那種方法最為簡便,雖然針對此題采用“比較密度法”是最為簡單的,如果題目還問“該球的空心體積是多大”時,則采用“比較體積法”最為快捷。
由此可見,通過一題多解,有利于培養學生加深對概念、規律、公式的理解和運用,提高學生的應變能力,促進知識的遷移,并達到指標治本,使之熟練和系統的掌握知識體系。

