重慶市交通運輸與經濟協調發展研究

李康奇，馮明兵

（重慶交通大學交通運輸學院，重慶 400074）

重慶作為我國第四個直轄市，位于長江中下游平原和青藏高原的過渡地帶，擁有廣闊的地域，在我國老工業基地里占據重要地位，工業輻射優勢強大，同時在我國長江上游自古以來也是重要的物資集散地。隨著“十二五”中后期的來臨，客觀上經濟系統需要與其各子系統發展相互協調，并以此促進“十三五”順利地規劃。因此，對重慶市經濟與交通運輸協調發展關系的研究就有了重要意義。

一、評價指標體系構建

（一）研究方法

交通運輸與經濟是兩個大系統，它們之間必然存在藕合性，評價兩者的協調性，也必然存在一定的復雜性，需要以多指標綜合評價來測度。多指標綜合分析實際上就是綜合各種不同的信息，經過變換和處理，使其能進行綜合評價。本文在實用性與科學性、特殊性和普遍性、靜態性和動態性相統一的原則下，建立評價指標體系，再根據文獻資料頻數分析法、典型分析法、DEA等方法進行計算，評價重慶市歷年的交通運輸與經濟協調發展程度。

（二）指標設計

重慶是中國重要的中心城市，西部地區重要的經濟增長極，西南地區綜合交通樞紐，城鄉統籌的特大型城市。鑒于此，對重慶交通運輸與經濟協調程度的研究主要包括交通運輸系統的交通基礎設施、交通運營情況、交通效益情況、交通可持續發展情況;經濟系統的經濟規模、經濟發展質量、經濟發展結構、經濟社會發展程度、經濟的外向度以及經濟的發展潛力等。

由于重慶市1997年正式成為直轄市，并且在2000年后才得到快速發展，所以本文以2004—2013年10年作為研究對象。典型相關分析要求因變量和自變量制和要小于等于數據的樣本量，因此根據文獻資料頻數統計法，保留頻率最高的指標，因此本文選擇的指標體系如表1所示。

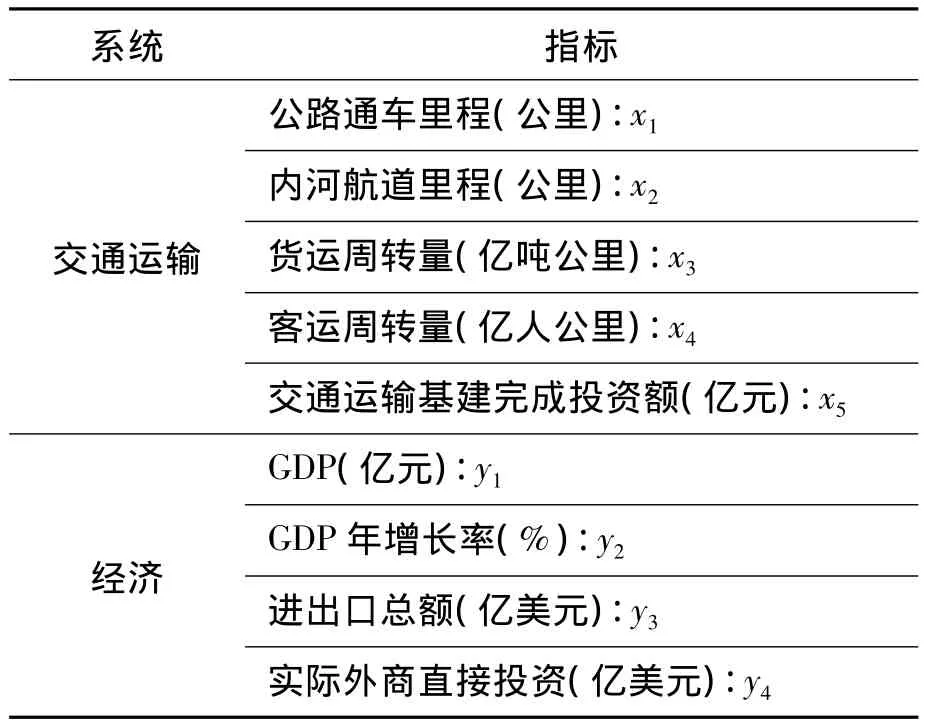
表1 典型相關分析的選擇指標

二、典型相關性分析

（一）實用性和原理

作為一種多元的統計方法，典型相關分析有很強的實用性。基于主成分的降維思想，典型相關分析生成一組新的線性組合，使得新生成的綜合變量能體現大部分的原始信息，此外和另一組新生成的綜合變量有很大的相關程度，這樣兩組的組合就成為第一對典型相關變量，然后繼續使用這種方法，找出接下來的幾對，直至典型相關變量之間存在的關系互不相關，由典型相關分析產生的系數本文稱為典型相關系數，該系數就是用來衡量兩系統之間相關性的系數。

本文設x=（x1，x2…，xp）′，y=（y1，y2…，yq）′兩個隨機變量，并且兩者相互關聯，基于主成分分析，分別找出代表性線性組合變量Ui，Vi。即

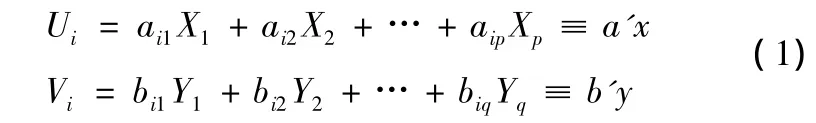
對于方差等于1的x，y線性函數a′x和b′y，求解的一組要使得其相關系數達到最大值，如果有常向量a1，b1并且滿足條件如下:

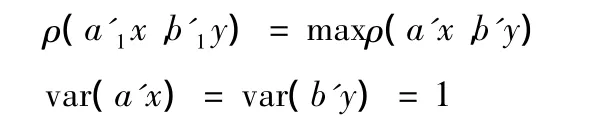
那么就可以稱 a′1x，b′1y為 x，y的典型相關變量，并且是第一對，用類似方法繼續求出接下來的幾對。x，y間線性相關狀態就可通過這些典型相關變量來反映。除此之外，還利用相關系數的絕對值來排列先后順序，一般情況下絕對值最大的就是第一對典型相關變量系數，下面依次是第二對…，0是檢驗綜合變量顯著性的數值，若相關系數顯著大于0，則有代表性，否則就沒有。這樣多重計算之后，就可以以少數典型相關變量來代替原來多組的研究，這樣既能方便計算，還能把握重點。

（二）結果及分析

采用SPSS軟件對上表的指標進行典型相關分析，并編寫如下程序:

計算結果以及分析如下:

表2中提出了4個典型相關系數，大小分別為1.000、0.970、0.949、0.480，表明就典型相關系數來說，前 3 個相關系數合格。再通過對4個典型相關系數的統計學意義進行檢驗，Sig在0.05內的只有前兩個相關系數，統計學意義明顯。綜合來說，通過相關系數及檢驗，前兩個系數合格。

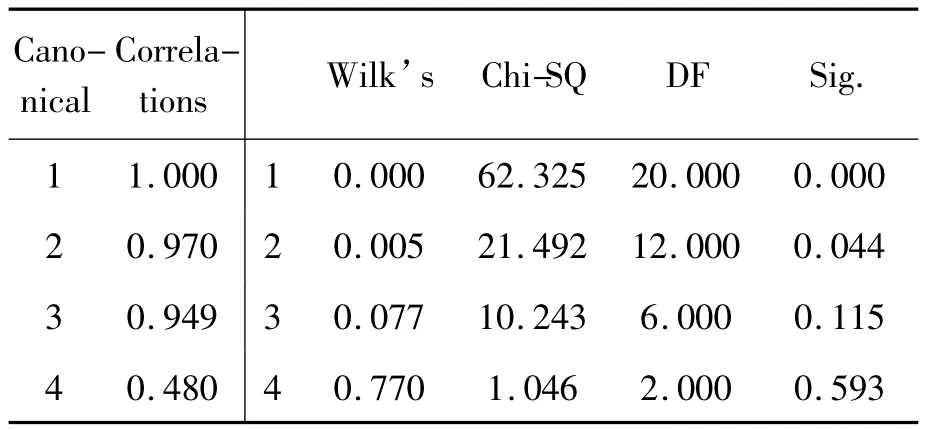
表2 典型相關系數表以及檢驗表

從表2可以看出第一變量組分別和自身以及典型變量相對的相關系數，從這里可以看出與第一對典型變量有著密切的關系。第二變量組分別和自身以及典型變量相對的相關系數，從這里可以看出與第一對典型變量有著密切的關系。綜合上述系數及檢驗，可得第一對典型變量關系更密切。

下面的分析結果是冗余度，它是對4個典型相關系數變異比例的描述，輔助決定典型相關系數保留的個數。從表4可以看出，第一組變量和第二組變量中都是第一典型變量能自我解釋的變異比較大，其他的均較小，這也可以間接說明第一典型變量可取，且解釋度比較大。

通過冗余度的計算以及分析，基本可以跟之前的檢驗結果相對應，經過多重分析，本文選取的對象為第一典型變量。

就相關系數來說，第一典型變量基本為1，說明交通運輸與經濟的第一典型變量有很大的影響。從單個系數來看，x3，x4，x5在交通運輸中起主要作用，系數分別為0.818、0.565、0.521，對應的為貨運周轉量、客運周轉量、交通運輸基建投資額。經濟起主要作用的為y1，系數是1.235，對應的是GDP。再比較符號，x6，x7，x8和y1都為正符號，這可以說明，交通基建投資和客貨運周轉量對經濟規模的影響相較于其他因素來說較大，并且是正相關的關系。立于宏觀的角度，經濟的規模從GDP來看最直接，衡量交通運輸的效果，可以從起點也就是交通運輸基建投資以及效果也就是客貨運周轉量來考量，這樣就說明交通運輸與經濟的相關關系非常顯著。

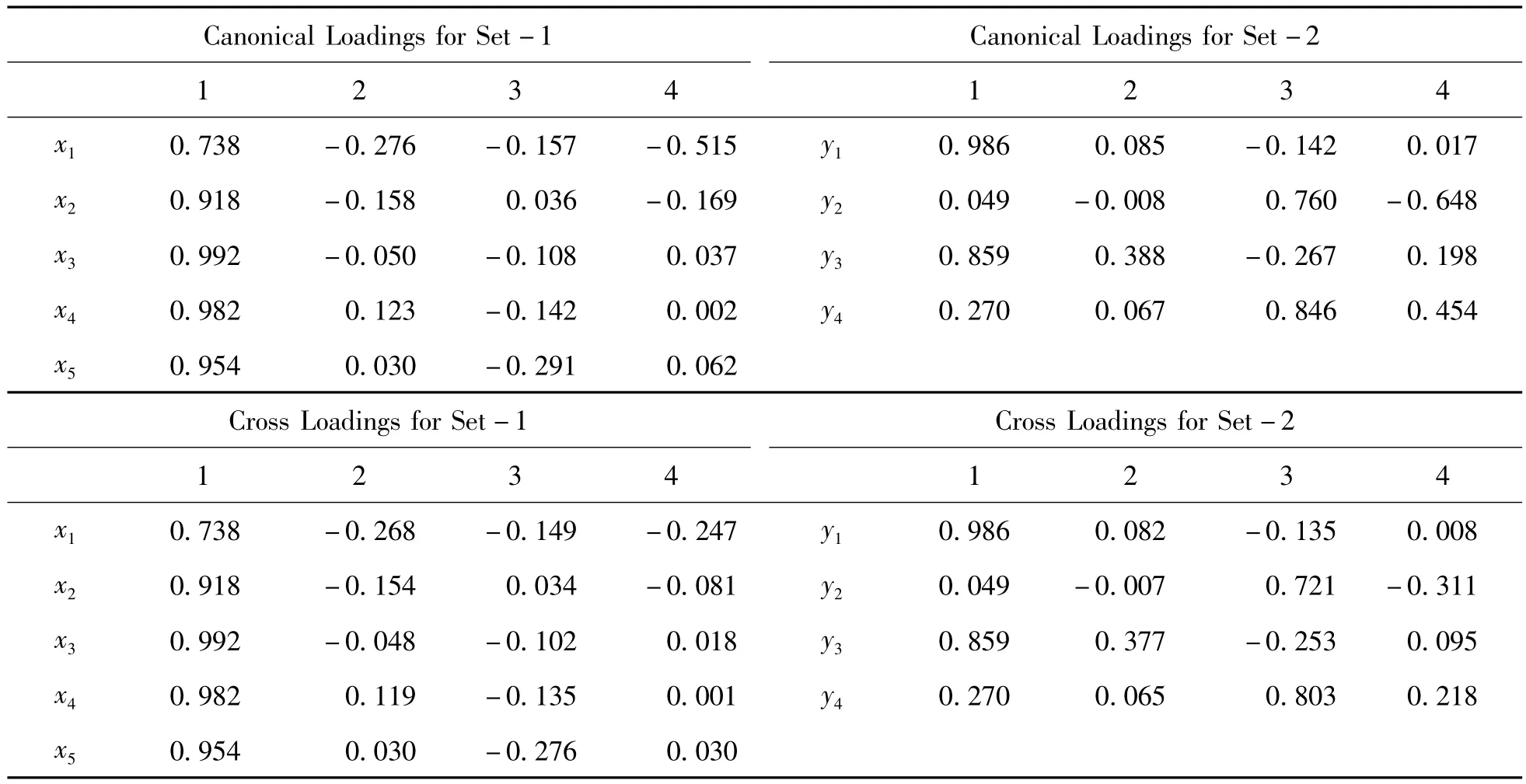
表3 第一變量組、第二變量組分別和典型變量的相關系數

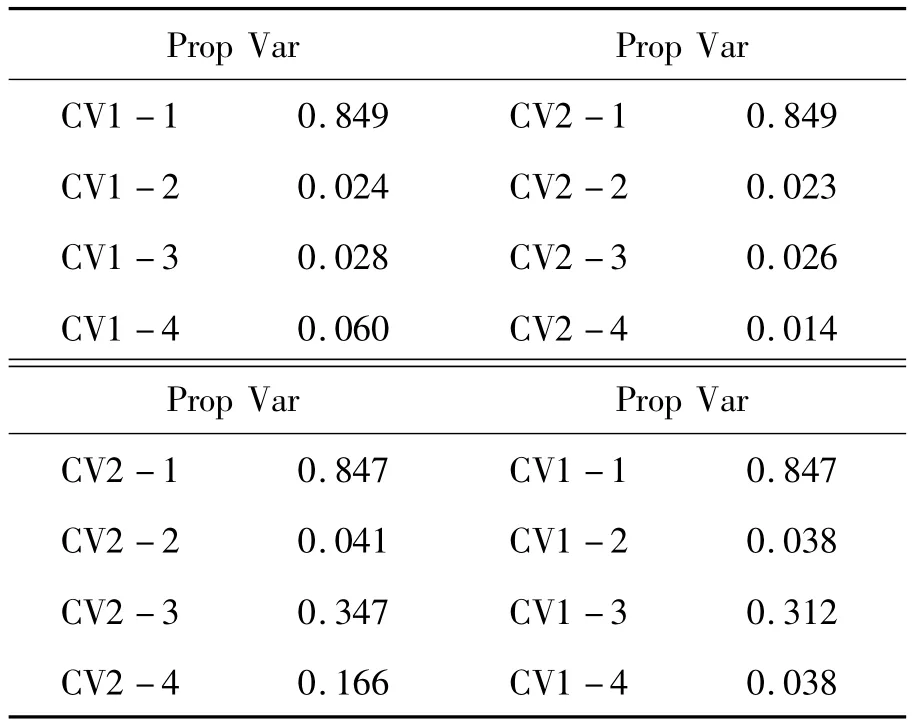
表4 第一、二組變量自身、相對解釋的比例

三、重慶交通運輸與經濟協調度研究

（一）DEA中CCR模型的構建

將重慶市2004—2013各年的交通運輸與經濟系統作為評估單元，記為Aj;

設X為重慶市交通運輸與經濟系統某一個的輸入，X={Xj，i=1，2，…，m};

設Y為重慶市交通運輸與經濟系統某一個的輸出，Y={Yk，k=1，2，…，s}。

則 Xij，Ykj為第 j個決策單元第 i、j種類型的輸入、輸出量。

CCR模型有以下定理與推論:

定理1:① 若θ=1，則DMUj0為弱DEA有效;② 若θ=1，且 s－=0，s+=0，則 DMUj0為 DEA 有效。

定理2:θ=1當且僅當DMU0為最大產出規模點。

推論1:若∑λj=1，則DMU0規模收益不變;∑λj＜1，則DMU0規模收益遞增;∑λj＞1，則DMU0規模收益遞減。

CCR模型經過一定的線性變換后，可以變為下面的線性變化模型:

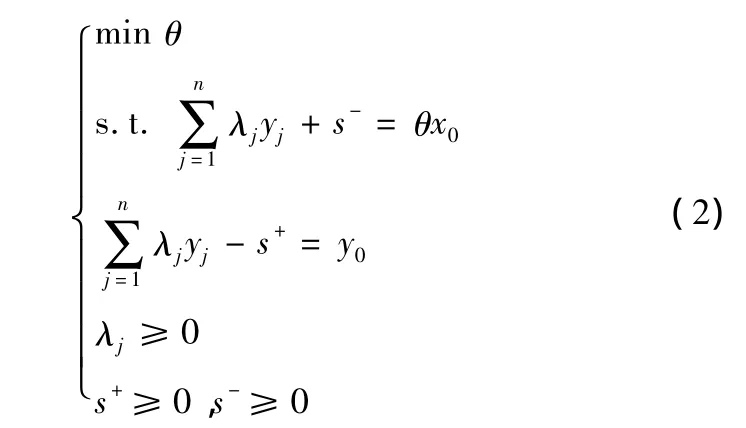
（二）指標選取

以2004—2013年為10個DMU，在對DEA原則遵循的基礎上，篩選第二章中的指標，并結合第三章典型相關分析，指標的篩選結果如表5。

表5 DEA分析指標

（三）有效性分析

利用matlab軟件編寫CCR模型程序進行計算。根據DEA的典型模型，由公式θ*=σ**s*，計算得出s*，具體如下:

1.以交通為輸入、經濟為輸出

由表6～表8所示，重慶市2004—2013年這10年內，只有2004年、2006年、2011年以及2012年4年的θ為1，有效率僅為40%;并且的值全為0的只有2011和2012年，表現的DMU為DEA有效;2004與2006年兩年表現為弱有效。其他6年，θ均不為1，屬于DEA無效。從總體上來看，θ的值均為0.9以上，即使沒得到最優，但是交通的付出對于經濟的促動也是相對較好的，形成了“交通→經濟”系統的良性協調發展趨勢，但是交通運輸對于經濟系統的推動還未達到最優狀態。從整體來看，可以明顯體現出2008年和2012年的經濟危機的影子。在經濟危機的情況下，大力發展交通運輸基礎建設以及提高服務水平，是為了帶動經濟的回升，但是過高的交通運輸投入并不一定能獲得與之相匹配的經濟回報。從θ值就可以看出，2008年以及2012年，其實只需要原來交通運輸投入的95%左右的投入就能獲得與之相匹配的經濟回報。

2.經濟為輸入，交通為輸出

如表9～表11所示，重慶市2004—2013年這10年內，只有2004年、2009年、2010年以及2013年4年的θ為1，有效率僅為40%，并且只有2011年和2012年的的值全為0，表明DMU為DEA有效;2004與2006年兩年表現為弱有效。其他6年，θ均不為1，屬于DEA無效。從總體上來看，θ的值均在0.9左右以及以上，即使沒得到最優，但是經濟的付出對于交通的促動也是相對較好的，形成了“經濟→交通”系統的良性協調發展趨勢，但是交通對于經濟系統的推動還未達到最優狀態。從整體來看，也明顯體現出2008年、2012年的經濟危機的影子。在經濟危機的情況下，大力發展交通運輸基礎建設以及提高服務水平，并不會出現發展不足的現象。但是在非經濟危機的情況下，雖然經濟情況表現還比較滿意，但是相對于交通的發展其實是過的，反過來說就是經濟即使有那么高的水平，但是交通運輸的發展卻是與之不相匹配的。

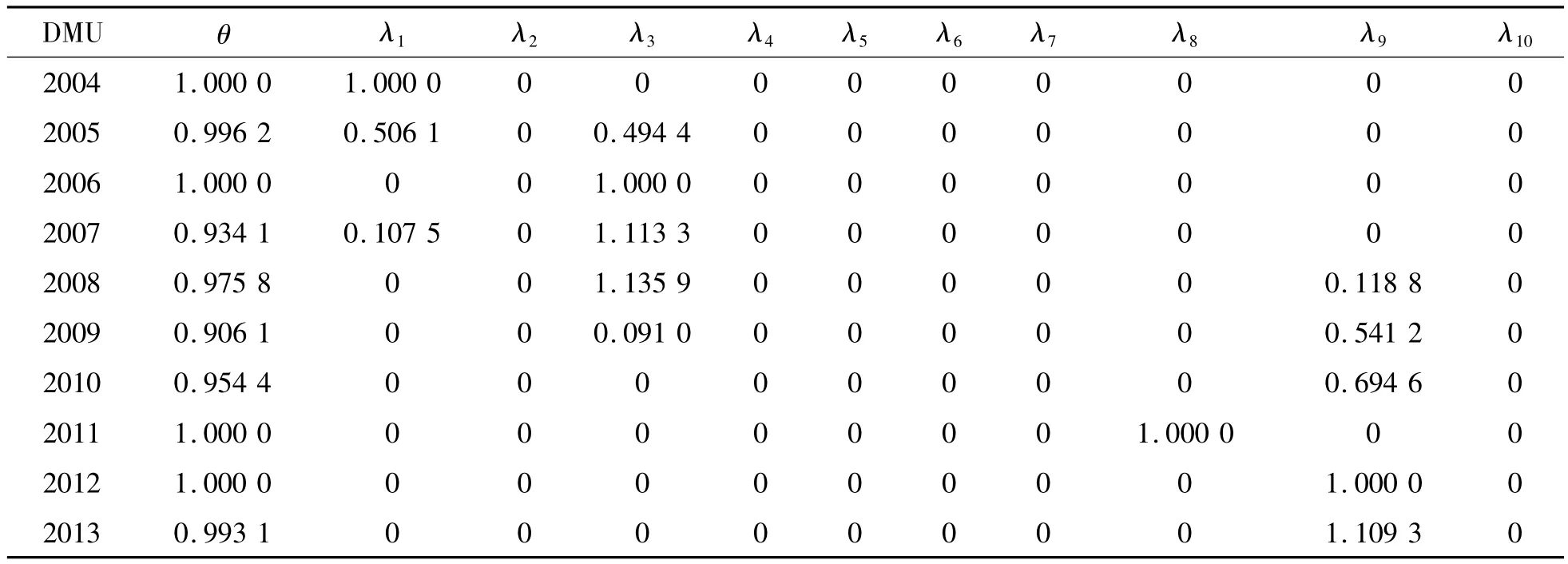
表6 交通－經濟規模有效性參數分析

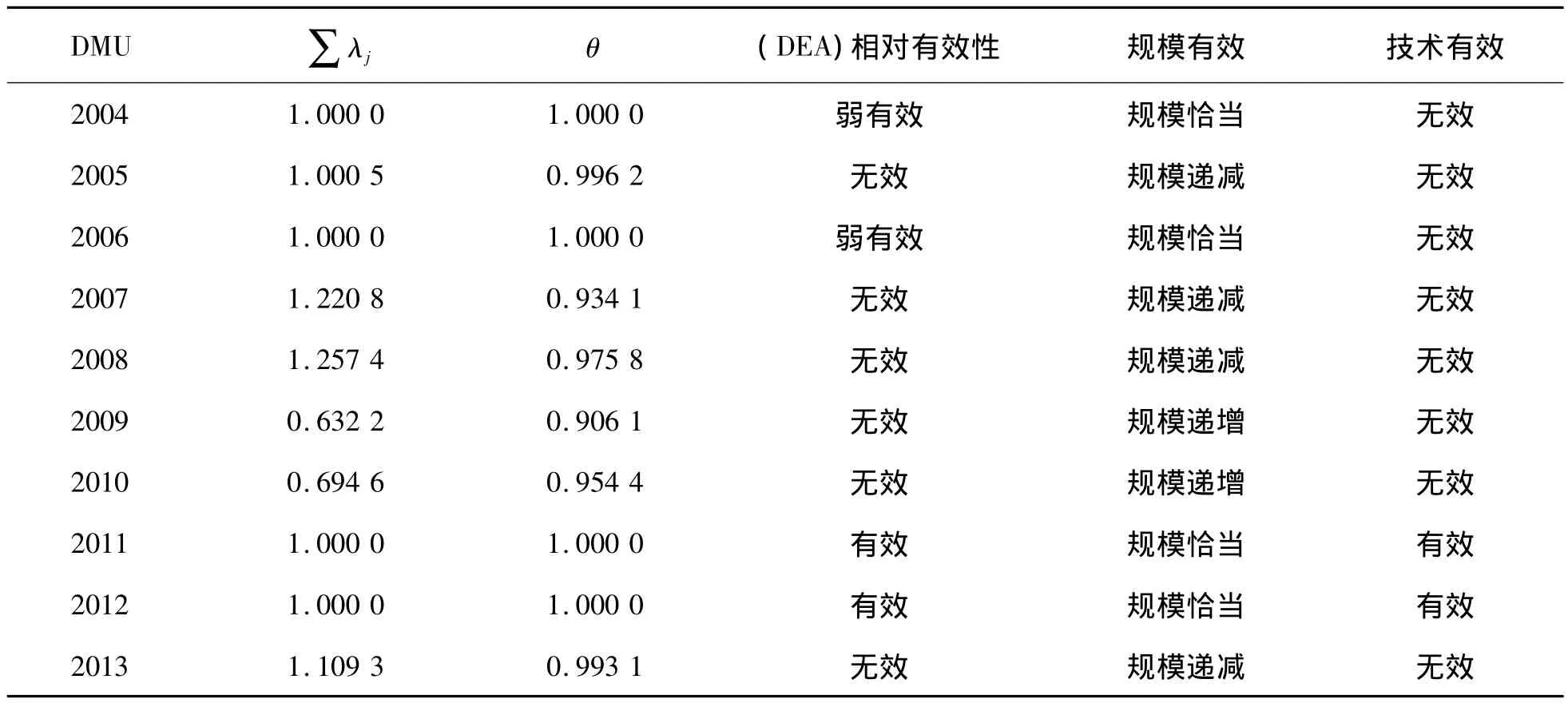
表7 交通－經濟規模、技術有效性分析

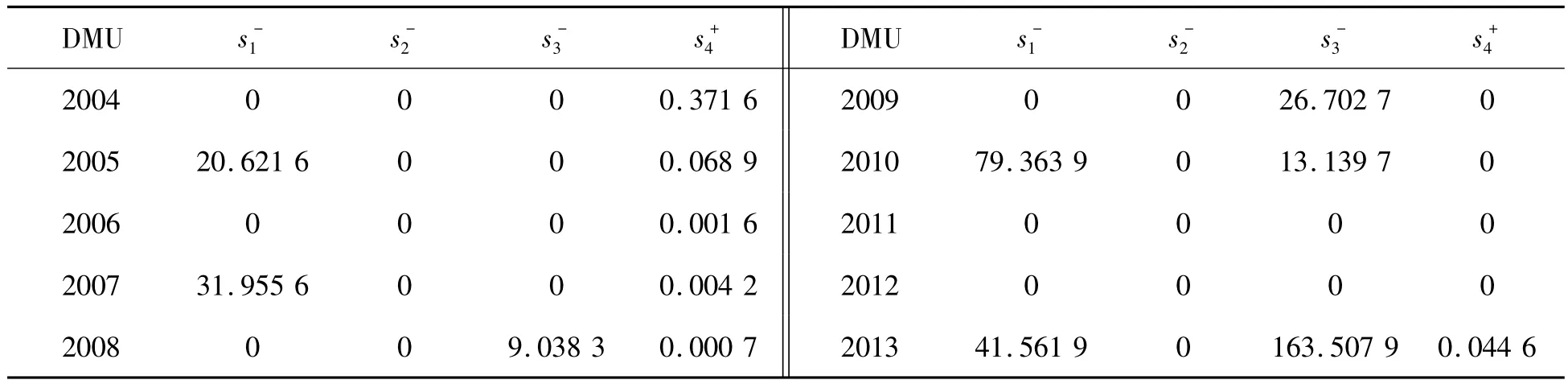
表8 交通－經濟技術有效性參數分析

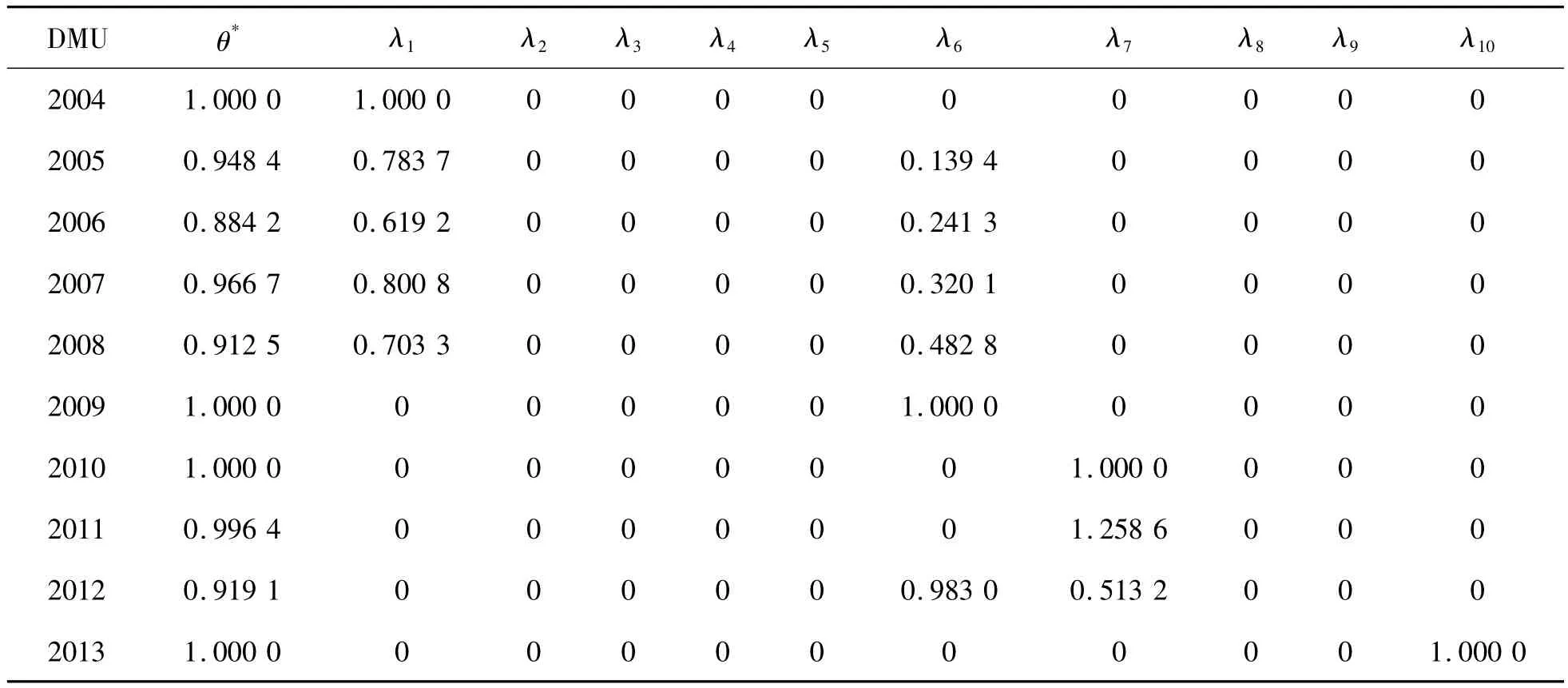
表9 經濟－交通規模有效性參數分析

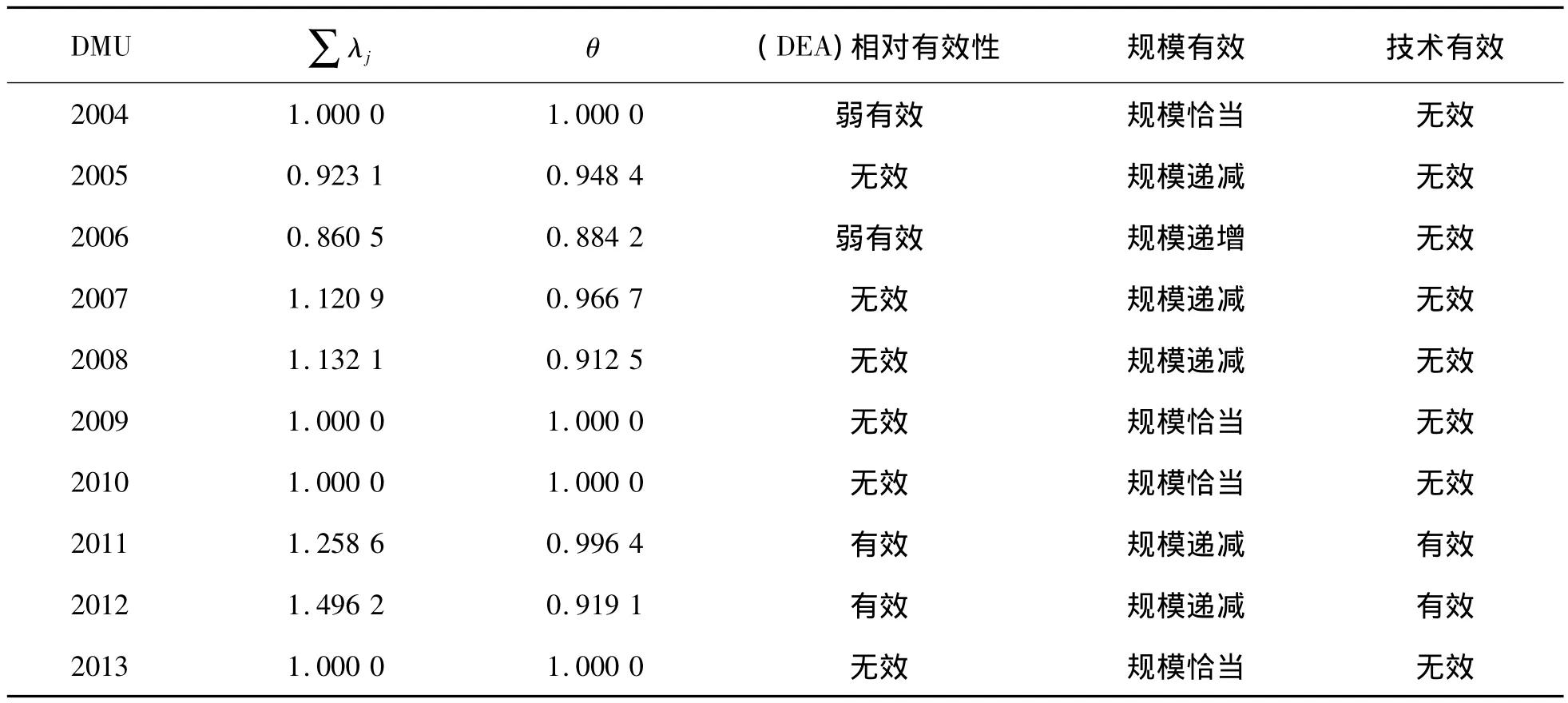
表10 經濟－交通規模有效性及技術有效性分析

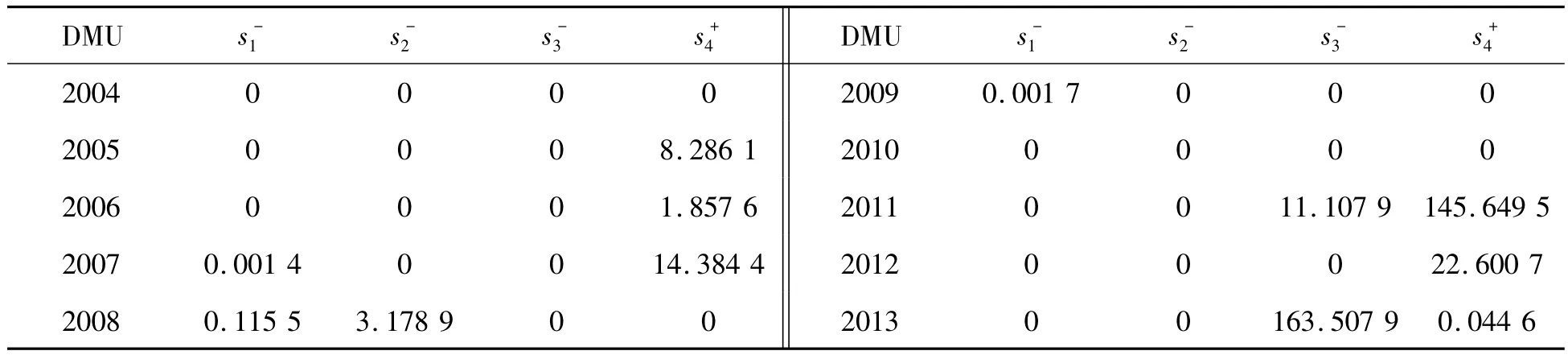
表11 經濟－交通技術有效性參數分析

（四）綜合協調度分析

在對重慶市交通運輸與經濟協調發展進行評價時，不能僅以“是”或“否”來對兩系統的狀態進行評價。更多時候，協調狀態處于協調與非協調之間，也可用基本協調這個詞來理解，表示并沒有達到最完美，但是又不至于很差，這種不上不下的狀態很明顯僅以“是”與“否”來評價有些欠妥。前面就提到過，協調度是一個外延不明確內涵明確的概念，所以用隸屬度這個模糊數學概念來闡述。隸屬度作為一個實數，取值區間為[0，1]，以隸屬函數來表示隸屬度度的變化規律。根據這個概念，建立重慶市交通運輸與經濟協調發展的協調度函數，隸屬函數定位為:

式中，狀態協調度為μ，重慶交通運輸與經濟互為投入產出的有效性指數為θ。從公式可以看出，有效性指數越大，協調度μ就越大。說明系統協調度發展程度越高。反之說明系統協調發展程度越低。

計算結果見表12。

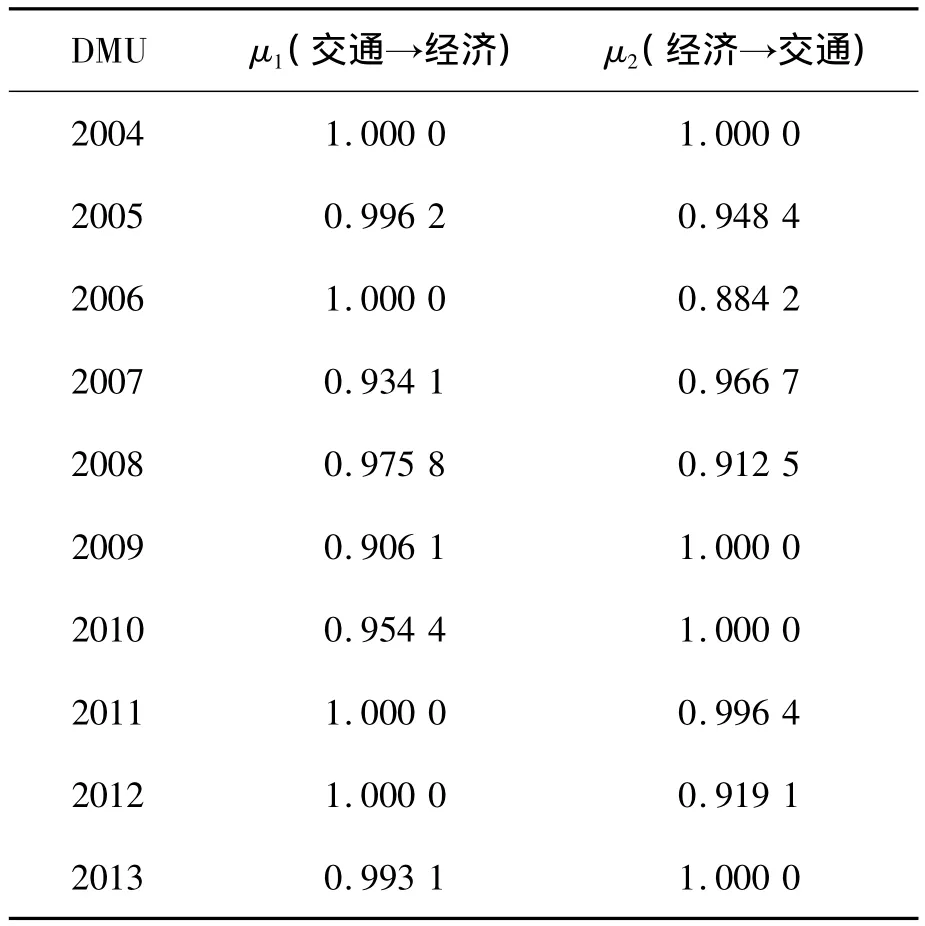
表12 2004—2013年重慶市交通運輸與經濟協調度計算結果

（五）靜態、動態協調度分析

系統之間相互協調發展程度的狀態協調度的計算，文獻中多采用公式:

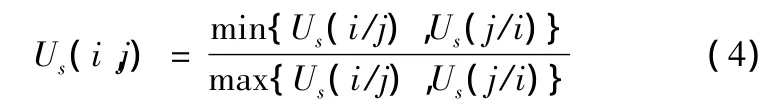
上式表明Us（i/j）與Us（j/i）的值越接近，Us（i，j）的值就越大，但是否代表系統間相互協調程度好呢?筆者認為，系統間相互協調程度好體現在兩個方面:Us（i/j）與Us（j/i）的值越接近越好;Us（i/j）與Us（j/i）本身越接近1越好。為彌補Us（i/j）與Us（j/i）本身大小的缺陷，本文選用另一公式，以綜合考慮兩方面的決定條件:

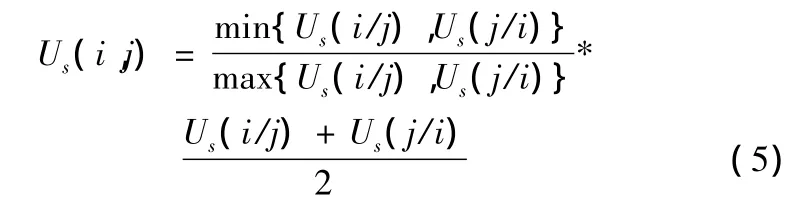
將數據帶入式（5）中，得出重慶市歷年交通與經濟的協調發展程度，如表13所示。

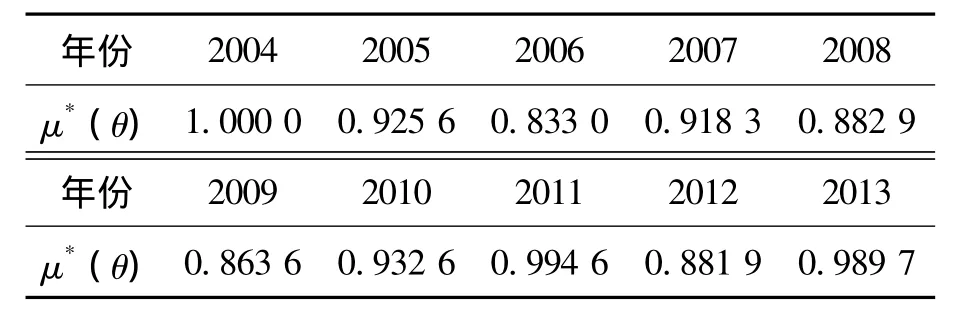
表13 靜態綜合協調度分析

靜態協調性的分析實際上是分析各年的協調發展性。但是，協調發展并非是靜止的，其過程也是動態的，所以在靜態分析的基礎上進行簡單動態分析，希望能夠看出重慶市2003—2014年交通運輸與經濟動態的協調發展程度。具體公式如下。

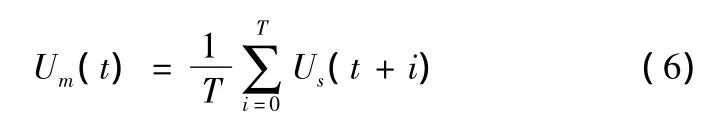
其中 Us（t+1），Us（t+2），…，Us（t+T），Us（t）是系統在2004—2013年度每年的靜態協調度，使用上述公式進行計算，得到表14的結果，并繪制成圖1。

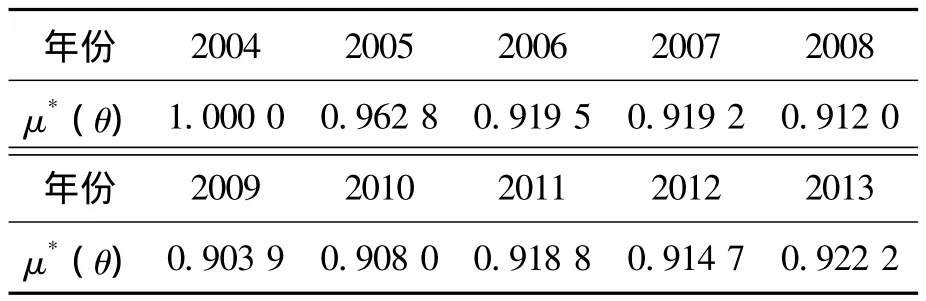
表14 動態協調度分析

從圖1中可以明顯看出協調程度的動態變化。這10年，全都都在基本協調及以上狀態，協調度都在0.90以上，長期過程起伏不大，比較流暢，而且都處于基本協調的閾值內，但都處于基本協調的中間限值，離協調還有一定的距離。

總體來看，重慶市交通運輸與經濟基本處于基本協調狀態，2008年前后由于經濟危機有較大波動外，相對也是較平穩，但是離協調還有一定的距離。相對于交通對于經濟的回報，經濟對于交通的回報略少。重慶市經濟發展快速，交通運輸的發展略顯滯后，交通問題開始受到關注。地方政府加大了對交通運輸的投入力度，經濟也有所回升，而且近幾年來一直保持著較高的水平。

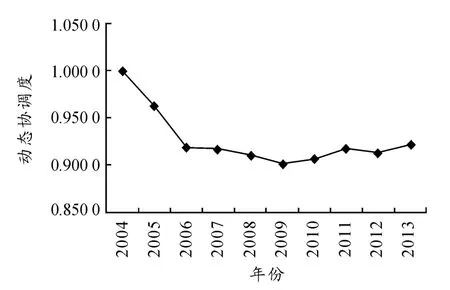
圖1 動態協調度圖

最后，需要特別強調，重慶市的交通運輸與經濟的協調度為1，并不代表兩系統之間已達到完美協調狀態，只是可以相對說明，在提取的2004—2013年這10年數據中是最好的，并且可以作為標準來衡量。

四、結論

隨著西部大開發的不斷推進，西部山區人民的生活水平不斷提高，同時人們對交通運輸的需求也日漸增加，而目前的交通現狀遠不能滿足需求。作為經濟的命脈，交通運輸在經濟中的支柱地位越來越明顯，用“社會離不開交通運輸”這句話來說一點都不為過。但是，在交通運輸發展迅猛的同時也帶來汽車尾氣污染環境、交通事故增加等問題。所以，交通運輸與經濟的協調發展，特別是山地城市重慶的兩系統的協調發展具有很強的社會意義。

[1] 王釗，陳乙酉，劉晗.重慶市區縣綜合競爭力研究[J].重慶大學學報:社會科學版，2015（21）:28－34.

[2] 何格，趙媛.土地市場和區域經濟耦合協調度分析[J].重慶大學學報:社會科學版，2015（21）:23 －27.

[3] 汪傳旭.交通運輸與經濟發展協調程度的定量評價[J].上海海運學院學報，1999（3）:96 －102.

[4] 汪傳旭.交通運輸與經濟協調發展分析模型及其應用[J].上海海運學院學報，1998（4）:26 －31.

[5] 武旭，胡思繼，崔艷萍，等.交通運輸與經濟協調發展評價的研究[J].北京交通大學學報:社會科學版，2005（4）:10－14.

[6] 孫雪花.公路交通與區域經濟協調發展評價研究[D].長沙:長沙理工大學，2009.

[7] 盧青.區域公路交通適應性研究[D].成都:西南交通大學，2011.

[8] 王曉蘭.江蘇省交通建設與區域經濟協調發展的實證研究[D].南京:南京理工大學，2007.