衛(wèi)星天線雙軸驅(qū)動機構(gòu)旋轉(zhuǎn)鉸磨損規(guī)律研究
張慧博,陳 軍,李甘霖,王興貴,程東起,田 艷
(哈爾濱工業(yè)大學(xué)(威海)飛行器動力學(xué)及仿真研究所,山東 威海 264209)
0 引言
磨損是機械設(shè)備失效的主要原因之一,是機械零部件的一種主要失效形式,也是引起其他后續(xù)失效的最初原因[1-2]。衛(wèi)星天線是航天器中實現(xiàn)星地、星間通信與數(shù)據(jù)傳輸?shù)闹匾M成部件,衛(wèi)星天線驅(qū)動機構(gòu)是實現(xiàn)衛(wèi)星天線實時跟蹤、小范圍調(diào)姿、定位等功能的一個關(guān)鍵組件[3-4]。雙軸驅(qū)動機構(gòu)主要功能是實現(xiàn)衛(wèi)星天線兩自由度的轉(zhuǎn)動,控制天線的精確指向,其指向精度是決定其使用壽命的關(guān)鍵指標(biāo)。目前航天器的發(fā)展趨勢是長壽命、高可靠性,衛(wèi)星的使用壽命由3~5年提高到10~12年,機構(gòu)磨損變得不可忽視。軸承與軸系間出現(xiàn)磨損間隙,將直接導(dǎo)致衛(wèi)星天線指向精度下降,嚴(yán)重時將使衛(wèi)星失效。為分析軸承與軸系間的磨損規(guī)律,常將其簡化為平面旋轉(zhuǎn)鉸,通過動力學(xué)仿真與磨損量計算,給出雙軸驅(qū)動機構(gòu)旋轉(zhuǎn)鉸的磨損規(guī)律。但磨損研究很少考慮機構(gòu)運行中的動態(tài)變化,認(rèn)為磨損率在磨損過程中是不變的,這與實際磨損規(guī)律差距較大,故計算準(zhǔn)確性較差。為提高磨損計算的精度,出現(xiàn)了以動力學(xué)仿真為主,結(jié)合磨損實驗的磨損規(guī)律研究方法:文獻(xiàn)[5]用動力學(xué)仿真法研究四桿機構(gòu)的磨損規(guī)律;文獻(xiàn)[6-7]基于ADAMS動力學(xué)仿真,研究磨損規(guī)律,提出了磨損壽命仿真預(yù)測方法;文獻(xiàn)[8]以Virtual.Lab Motion為平臺對某履帶車輛同步器進(jìn)行仿真,研究其磨損規(guī)律。但由于磨損問題的復(fù)雜性,現(xiàn)有研究方法只能根據(jù)具體構(gòu)件進(jìn)行分析,無通用的磨損規(guī)律。另外受實驗條件的限制,無法進(jìn)行微重力條件下的整機磨損實驗。為此,本文用仿真法對某空間驅(qū)動機構(gòu)旋轉(zhuǎn)較磨損規(guī)律進(jìn)行了研究。
1 動力學(xué)建模與仿真
1.1 運動副間隙描述
含間隙運動副在運行過程中不可避免會發(fā)生接觸碰撞,這使含間隙系統(tǒng)有兩種拓?fù)錉顟B(tài):一種是不含任何約束的自由運動狀態(tài),另一種是單邊約束運動狀態(tài)[9]。含間隙的變結(jié)構(gòu)系統(tǒng)總在自由運動和單邊約束兩種狀態(tài)間相互切換,判斷系統(tǒng)當(dāng)前處于的狀態(tài),以及對含間隙運動副接觸碰撞過程的正確描述,是含間隙動力學(xué)建模的關(guān)鍵。
對衛(wèi)星天線雙軸驅(qū)動機構(gòu)旋轉(zhuǎn)鉸,間隙Δ用軸承與軸半徑之差描述,則

式中:R1為軸承(大圓)半徑;R2為軸(小圓)半徑。如圖1所示。
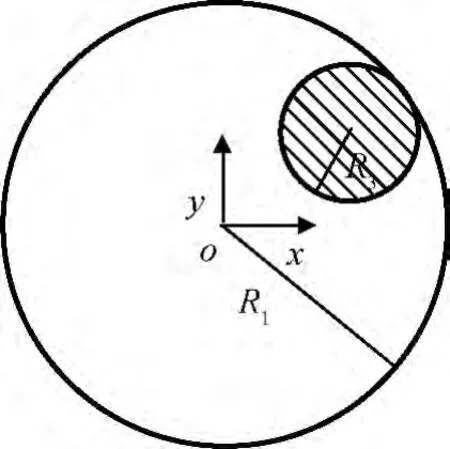
圖1 含間隙轉(zhuǎn)動副模型Fig.1 Revolute joint with clearance
為正確描述接觸碰撞過程,判斷系統(tǒng)當(dāng)前處于何種狀態(tài),在旋轉(zhuǎn)鉸中心處建立坐標(biāo)系o-xy,設(shè)軸的中心坐標(biāo)為(x1,y1),則接觸變形量
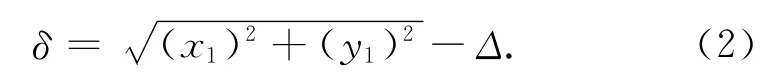
由式(2)可知:當(dāng)δ≤0時,系統(tǒng)處于自由運動狀態(tài);當(dāng)δ>0時,系統(tǒng)處于單邊約束運動狀態(tài)。
1.2 運動副間隙接觸碰撞模型
根據(jù)運動副元素的相對運動關(guān)系的不同假設(shè),對間隙碰撞問題的處理方法主要有二狀態(tài)模型、三狀態(tài)模型、連續(xù)接觸模型三種。其中二狀態(tài)模型認(rèn)為:在運動過程中運動副元素處于分離和接觸兩種狀態(tài),其碰撞特性用無質(zhì)量等效彈簧阻尼模型描述,該模型假定碰撞為點接觸,碰撞力通過接觸點作用于兩體,碰撞力大小取決于等效彈簧的剛度和阻尼特性。等效彈簧阻尼模型雖然是一種近似分析方法,但它易與機構(gòu)動力學(xué)方程結(jié)合,且一般有較好的精度,在含間隙機構(gòu)動力學(xué)分析中應(yīng)用廣泛。
用非線性等效彈簧阻尼模型建立旋轉(zhuǎn)鉸間隙接觸碰撞模型,其廣義形式可表示為
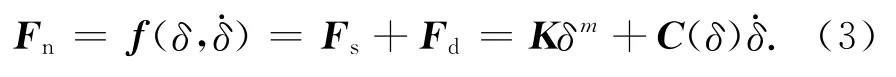
式中:Fn為接觸點處法向接觸力;Fs為等效彈簧力;Fd為等效阻尼力;K為等效接觸剛度;δ分別為運動副元素間的接觸變形量和法向相對速度;C(δ)為與δ有關(guān)的阻尼因子;m為力指數(shù),由實驗確定,通常金屬與金屬材料碰撞取1.5。
Fn可用Hertz接觸模型計算;Fd主要反映碰撞過程的能量損耗特性,同時保證接觸力Fn滿足碰撞過程的邊界條件
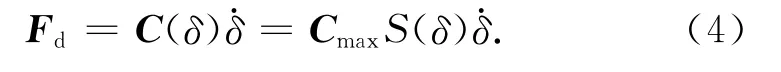
式中:Cmax為最大阻尼系數(shù),由實驗確定;S(δ)是為防止碰撞過程中阻尼力的不連續(xù)引入的函數(shù),且
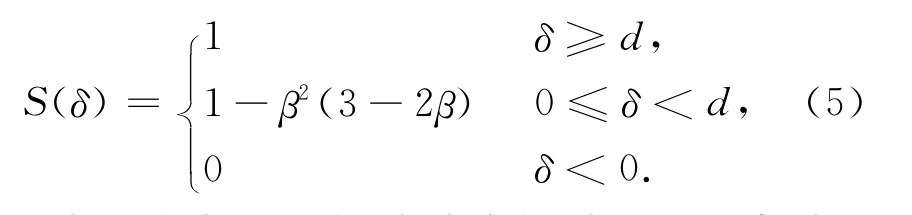
此處:d為最大嵌入深度,它決定何時阻尼力達(dá)到最大;β=δ/d。
1.3 動力學(xué)仿真分析
本文以ADAMS動力學(xué)仿真軟件為平臺,利用虛擬樣機技術(shù)建立衛(wèi)星天線雙軸驅(qū)動機構(gòu)動力學(xué)仿真模型,如圖2所示。通過靜態(tài)校驗和運動學(xué)校驗,保證無間隙虛擬樣機的可信性。然后將運動副間隙的接觸碰撞模型嵌入動力學(xué)模型,用實驗確定接觸碰撞模型的參數(shù),以保證含間隙雙軸驅(qū)動機構(gòu)虛擬樣機的可信性。
雙軸驅(qū)動機構(gòu)主要由縱軸、橫軸兩個旋轉(zhuǎn)鉸組成,縱軸帶動整個驅(qū)動機構(gòu)轉(zhuǎn)動,其旋轉(zhuǎn)鉸承受徑向力較大。用動力學(xué)仿真研究其動態(tài)特性,設(shè)仿真參數(shù)為 間 隙 0.2mm,轉(zhuǎn) 速 3.0 (°)/s,剛 度 1.7×107N/m,阻尼175.0N·s/m,仿真所得運動軌跡、接觸變形量、徑向速度和接觸力分別如圖3~6所示。

圖2 衛(wèi)星天線雙軸驅(qū)動機構(gòu)虛擬樣機模型Fig.2 Virtual prototype model of two-axis-position mechanism for satellite antenna

圖3 軸中心運動軌跡Fig.3 Axial center path
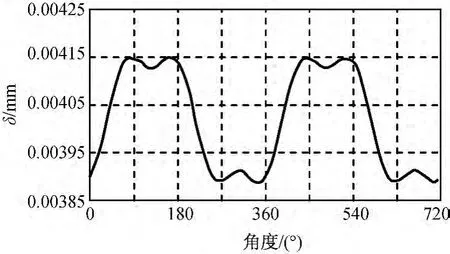
圖4 接觸變形量Fig.4 Deformation
由圖4可知:在驅(qū)動機構(gòu)平穩(wěn)運行時,δ始終大于0,則旋轉(zhuǎn)鉸中軸與軸承處于連續(xù)接觸狀態(tài)。由圖6可知:接觸力為周期變化,且幅值較小,旋轉(zhuǎn)鉸周向受力相對均勻,可取接觸力的平均值作為該工況下的旋轉(zhuǎn)鉸受力,同時近似認(rèn)為旋轉(zhuǎn)鉸處為均勻磨損。
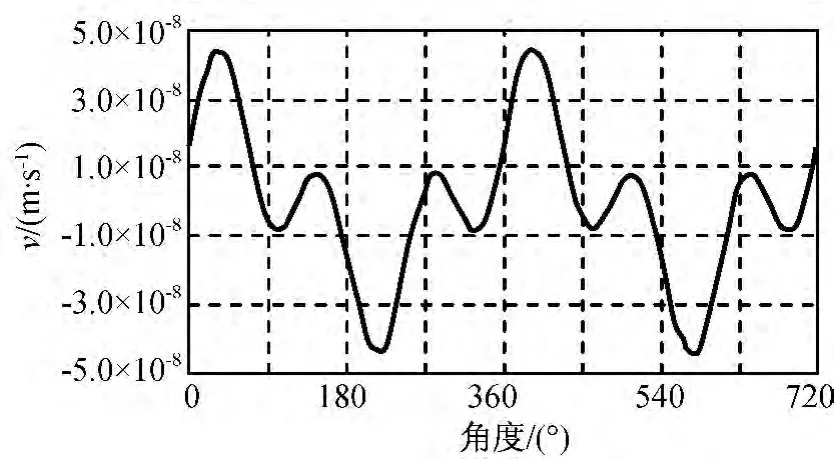
圖5 徑向速度Fig.5 Radial velocity
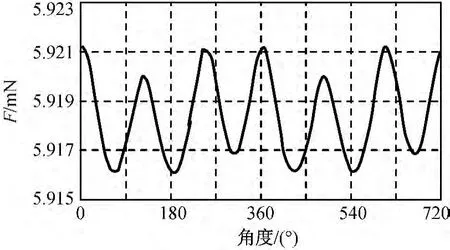
圖6 接觸力Fig.6 Contact force
接觸力平均值隨磨損間隙而變,在磨損過程中的變化規(guī)律是計算磨損量的動力學(xué)基礎(chǔ)。因假設(shè)旋轉(zhuǎn)鉸為均勻磨損,改變運動副間隙以模擬磨損間隙變化,進(jìn)行動力學(xué)仿真實驗,得到不同磨損間隙的接觸力平均值如圖7所示。
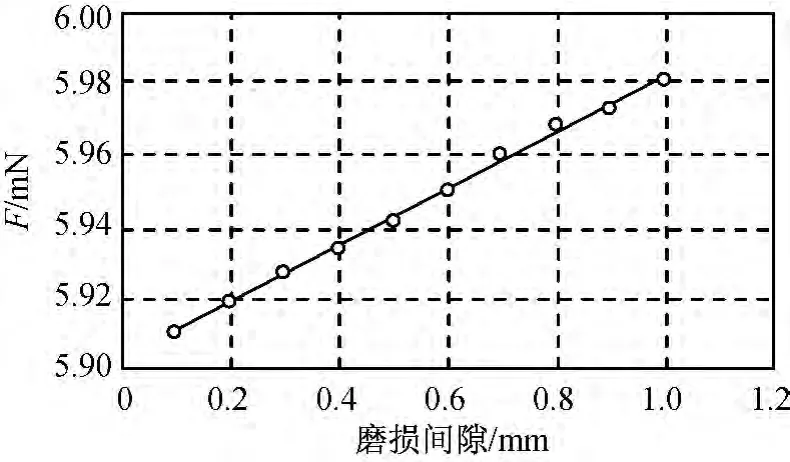
圖7 接觸力變化規(guī)律Fig.7 Contact force variation
由圖7可知:運動副間隙隨著機構(gòu)的磨損不斷變大時,旋轉(zhuǎn)鉸接觸力近似成線性增大。由多項式擬合,額定工況下雙軸驅(qū)動機構(gòu)縱軸旋轉(zhuǎn)鉸處接觸力
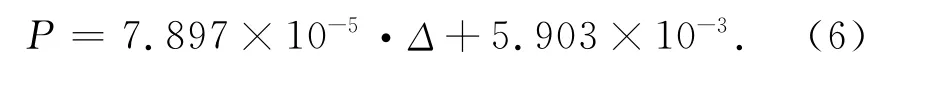
2 磨損數(shù)學(xué)模型
磨損過程是一個極其復(fù)雜的過程。現(xiàn)階段的磨損機理研究不充分,對磨損過程很難建立詳細(xì)的數(shù)學(xué)模型。對于運動副磨損的研究,多是根據(jù)實驗確定磨損的宏觀規(guī)律,用磨損率和各因素之間的簡單函數(shù)關(guān)系表達(dá)。根據(jù)摩擦學(xué)理論同時結(jié)合相關(guān)的磨損實驗,可建立磨損過程的數(shù)學(xué)模型,磨損率γ可表示為

式中:W為磨損量;t為磨損時間;P為摩擦面的表面接觸壓力;V為運動副構(gòu)件間的相對速度;Tk為摩擦表面溫度;Kw為摩擦表面形態(tài)、潤滑狀態(tài)及材料特性等因素[5]。為研究磨損量的極限值,認(rèn)為磨損在干摩擦條件下進(jìn)行,忽略潤滑、溫度等因素的影響。根據(jù)當(dāng)前干摩擦較為通用的磨損率表達(dá)式,可得經(jīng)驗公式

式中:Kw,m,n為與材料特性有關(guān)的參量,由實驗獲得[10]。則磨損量可表示為
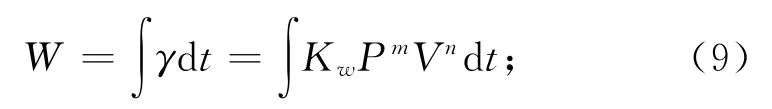
相應(yīng)的磨損深度
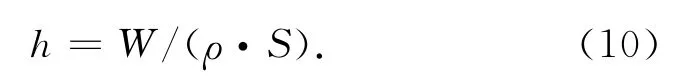
式中:ρ為材料密度;S為磨損面積。
根據(jù)磨損深度的函數(shù)表達(dá)式和接觸力變化函數(shù),可建立磨損過程的數(shù)學(xué)模型。為提高計算速度,采用分段近似方法,在一個時間積分段中將壓力和速度作為常數(shù)處理。建立數(shù)學(xué)模型
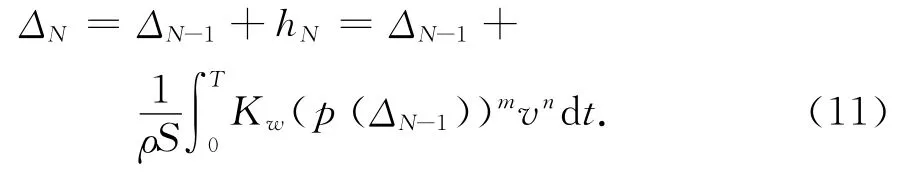
式中:N為運行次數(shù),N≥1,取旋轉(zhuǎn)鉸相對轉(zhuǎn)動1周為運行1次;ΔN為運行N次的磨損間隙(Δ0為初始間隙);hN為運行第N次的磨損深度;S=2π(R+ΔN-1)b;R為旋轉(zhuǎn)鉸處軸承內(nèi)徑;b為軸承寬度;p(ΔN-1)為間隙為ΔN-1時的接觸力;v為軸與軸承的相對速度,由衛(wèi)星天線的運行工況決定;T為積分時間,即運行1次的時間。
根據(jù)數(shù)學(xué)模型,在MATLAB軟件中編制程序,進(jìn)行遞推運算,可得與運行次數(shù)N相關(guān)的磨損間隙的變化規(guī)律。將N換算為時間,即為驅(qū)動機構(gòu)運行過程中的磨損規(guī)律。
3 旋轉(zhuǎn)鉸磨損規(guī)律分析
結(jié)合接觸力變化函數(shù)和磨損數(shù)學(xué)模型,研究雙軸驅(qū)動機構(gòu)縱軸旋轉(zhuǎn)鉸的磨損規(guī)律。設(shè)磨損參數(shù)為:T=120.0s;m=1.5;n=2.0;Kw=0.92;Δ0=0.05mm,仿真所得磨損過程如圖8所示。
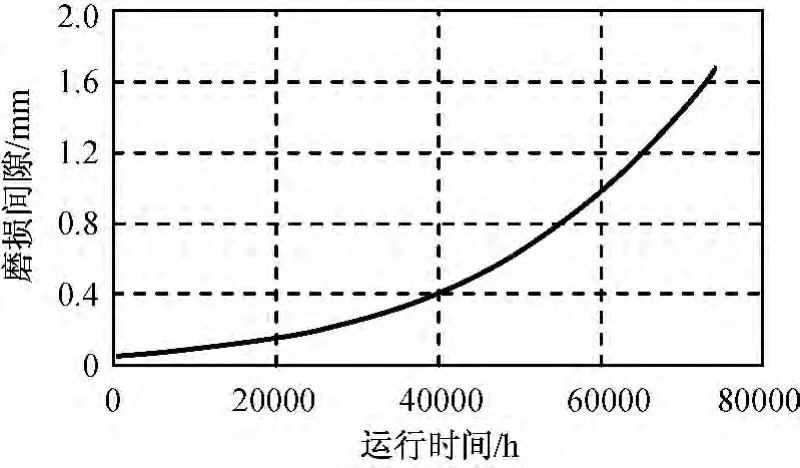
圖8 磨損過程Fig.8 Wear curve
由圖8可知:在運行初期,運動副間隙小,接觸力較小,磨損率基本保持不變,處于穩(wěn)定磨損階段,此時機構(gòu)運行穩(wěn)定,驅(qū)動機構(gòu)指向精度能得到保證;運行一段時間后,磨損量不斷累加,運動副間隙增大,接觸力隨之增大,導(dǎo)致磨損率迅速增加,磨損越來越劇烈,工作條件急劇惡化,這對驅(qū)動機構(gòu)的位置誤差、姿態(tài)誤差及速度誤差都有影響,會導(dǎo)致衛(wèi)星天線指向精度迅速下降,甚至衛(wèi)星天線完全失效。因此,根據(jù)驅(qū)動機構(gòu)旋轉(zhuǎn)鉸的以上磨損規(guī)律,可進(jìn)行合理的機構(gòu)設(shè)計和控制系統(tǒng)設(shè)計,盡可能降低磨損間隙變化對系統(tǒng)運行的影響,保證衛(wèi)星天線指向精度。
4 結(jié)束語
本文對某衛(wèi)星天線雙軸驅(qū)動機構(gòu)旋轉(zhuǎn)鉸的磨損規(guī)律進(jìn)行了研究。用虛擬樣機技術(shù)建立并驗證無間隙整機模型,結(jié)合構(gòu)件的接觸碰撞實驗和磨損實驗,建立合理的旋轉(zhuǎn)鉸接觸碰撞模型和磨損模型。將接觸碰撞模型嵌入虛擬樣機,保證含間隙虛擬樣機的可信性。用動力學(xué)仿真研究了旋轉(zhuǎn)鉸的動態(tài)特性及接觸力在磨損過程中的變化規(guī)律,給出了旋轉(zhuǎn)鉸的磨損規(guī)律。在虛擬樣機建立合理,并有構(gòu)件的接觸碰撞實驗和磨損實驗作為支持的情況下,可保證磨損規(guī)律的可信性。該方法降低了實驗難度,所得的磨損規(guī)律可為雙軸驅(qū)動機構(gòu)的性能評估與優(yōu)化設(shè)計提供指導(dǎo)。
[1] 劉英杰,成克強.磨損失效分析[M].北京:機械工業(yè)出版社,1991.
[2] 任 和,馮元生,賈少膨.機構(gòu)磨損的模糊可靠性計算研究[J].機械科學(xué)與技術(shù),1998,17(1):46-48.
[3] 孫 京,馬興瑞,于登云.星載天線雙軸定位機構(gòu)指向精度分析[J].宇航學(xué)報,2007,28(3):545-550.
[4] 田 浩,趙 陽,孫 京,等.雙軸定位點波束天線波束指向計算[J].宇航學(xué)報,2007,28(5):1215-1218.
[5] FLORES P.Modeling and simulation of wear in revolute clearance joints in multibody syste-ms[J].Mechanism and Machine Theory,2009,44:1211-1222.
[6] 張景柱,徐 誠,胡良明,等.基于ADAMS的操縱摩擦件壽命仿真預(yù)測方法[J].機械科學(xué)與技術(shù),2007,26(6):767-769.
[7] 張箭鋒,鄭 堅,馬吉勝.基于ADAMS的某型炮閂系統(tǒng)關(guān)鍵件磨損壽命計算[J].機械工程與自動化,2009(5):114-118.
[8] 王 炎,王玉軍,張 磊,等.某履帶車輛同步器工作過程仿真及磨損壽命預(yù)測[J].軍械工程學(xué)院學(xué)報,2009,21(6):26-30.
[9] ZHAO Y,BAI Z F.Dynamics analysis of space robot manipulator with joint clearance[J].Acta Astronautica,2010,10:1016-1025.
[10] 溫詩鑄,黃 平.摩擦學(xué)原理[M].北京:清華大學(xué)出版社,2008.

