基于LAP-GA 的多軍事物流配送中心選址

盧海容，金曉輝，劉士通，肖學福，吳會博

(1.軍事交通學院 研究生管理大隊，天津300161;2.軍事交通學院 軍事物流系，天津300161;3.軍事交通學院 軍事交通運輸研究所，天津300161)

軍事物流配送，作為軍事物流的末端活動，根據部隊用戶的需求，將軍事物資送達到指定地點。軍事物流配送中心，作為軍事物資配送業務的場所或組織［1］，是從各倉庫等供貨單位接收大量軍事物資，按照部隊用戶的要求，對這些物資進行卸載、分揀、加工等軍事物流作業，最終將處理后的軍事物資送達給各用戶，為實現軍事物流配送的精確化和集約化，提供了有力的支撐。軍事物流配送中心作為軍事物流環節的樞紐和中心，為保障部隊用戶發揮了重要作用［2］。影響其職能發揮的首要問題是如何科學選址，尤其是多軍事物流配送中心選址。傳統的多軍事物流配送中心選址理論中，存在很多不足的地方，如沒有把倉庫至軍事物流配送中心的運輸成本、軍事物流配送中心至用戶的配送成本以及軍事物流配送中心的建設成本有機結合起來，統籌考慮等，造成了配送時間長、配送成本高、配送資源浪費等問題，嚴重影響軍事物流配送效果。

針對上述的問題，為改善傳統多軍事物流配送中心選址問題中的不足，方便模型建立，將問題簡化如下:在某一地區，周圍有m個倉庫，儲存一定量的軍事物資，有p個部隊用戶需要大量的軍事物資，需建立數個軍事物流配送中心以滿足部隊用戶對物資的需求(如圖1 所示)。現已知n個備選地址作為軍事物流配送中心的建設地址，通過相關統計得到各倉庫到備選地址的單位運費、各倉庫的年最大運量、軍事物流配送中心的年最大運量、軍事物流配送中心的建設費用、備選地址到部隊用戶的配送費用以及用戶年需求量等數據。要求根據現有數據，進行多軍事物流配送中心選址，并且計算出分配倉庫到軍事物流配送中心的年運量以及軍事物流配送中心到各部隊用戶的年運量。

圖1 物資流向示意

1 問題分析

最早的選址問題是由Weber 于1909 年提出的［3］，他根據倉庫和用戶之間的最短距離來確定倉庫的位置。配送中心選址方法可分為連續型模型選址、離散型模型選址、德爾菲(Delphi)專家咨詢法選址3 種方法［4］。其中離散型模型選址方法，是根據相應的目標函數，配送中心僅在有限的備選地址中選取，代表方法是定位-分配問題(location-allocation problem，LAP)模型，它在理論上是比較完善的，考慮物流總費用的構成比較全面，包括發生點到物流中心、物流中心到接收點、發生點到接收點的運輸費用以及物流中心的建設費用和運營費用［5］。

應用連續型模型選址方法，模型過于簡單，僅能解決在運輸費用最小化的前提下單個配送中心選址;應用離散型模型選址方法，變量和約束條件都比較多，難以對模型求解;應用Delphi 專家咨詢法選址，只能定性的分析選址問題，對多配送中心選址問題就無能為力了。本文建立LAP 模型，并利用遺傳算法，通過Matlab 中的gatool 對該模型進行系統分析和快速求解。建立以倉庫至軍事物流配送中心的運費、軍事物流配送中心至用戶的運費、建設軍事物流配送中心成本之和最低為目標函數，以不超過最大運力和滿足用戶需求為約束的LAP 模型，全面考慮了軍事物流配送總費用的構成。

2 模型建立

2.1 模型假設

對模型做如下假設:①根據倉庫到軍事物流配送中心的距離等因素，可以估算出把軍事物資從倉庫運輸到軍事物流配送中心的單位費用矩陣，同理可以得到把軍事物資從軍事物流配送中心配送到用戶的單位費用矩陣;②僅在給定的被選地址中選擇一部分建立軍事物流配送中心;③軍事物流配送費用與運量成正比;④各用戶的年需求量已知，且為常數;⑤各倉庫的年最大運量已知，且為常數;⑥備選軍事物流配送中心的年最大運量已知，且為常數。

2.2 模型建立

要求選址成本最小，即由倉庫至軍事物流配送中心的年運輸費用、軍事物流配送中心至用戶的年配送費用、軍事物流配送中心建設費用組成的軍事物流配送中心選址總費用最小，并以此為目標函數，則有

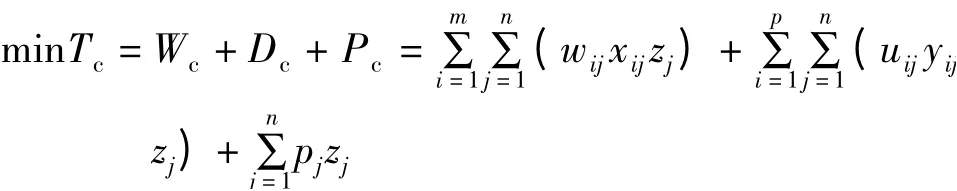
式中:Tc為總成本;Wc為倉庫運輸成本;Dc為配送成本;Pc為配送中心建設成本;wij(i=1，2，…，m;j=1，2，…，n)為m倉庫至n配送中心運輸量分配額;xij為m倉庫至n配送中心運輸單價;zj為是否選擇第j個備選地址作為軍事物流中心(0 表示不選，1 表示選擇);uij(i=1，2，…，p;j=1，2，…，n)為n配送中心至p用戶的運量分配額;yij為n配送中心至p用戶的配送單價;pj(j=1，2，…，n)為備選地址成本單價。

必須在滿足以下約束條件的基礎上，多軍事物流配送中心選址成本最小才有實際意義。①選址各倉庫運至各軍事物流配送中心的實際年運量不能超過該倉庫最大年運量，即Wt≥Wrt≥0;②各軍事物流配送中心至各部隊用戶的實際年配送量不超過該配送中心的最大年配送量，即Dt≥Drd≥0;用戶獲得實際運量不能低于所需的運量，即Urg≥Ur≥0;③0 或1 表示是否選擇第j個備選地址作為軍事物流配送中心建設地址，即zj=0 或1;④倉庫至軍事物流配送中心年總運量不小于軍事物流配送中心至用戶的年總運量，軍事物流配送中心至用戶的年運量不小于用戶實際獲得年總運量，即sum(Wrt)≥sum(Drd)≥sum(Urg)≥0。

2.3 模型實現

由于多軍事物流配送中心選址LAP 模型的變量和約束條件多且復雜，用一般的算法，如線性規劃、0—1 規劃等，實現模型的求解比較困難。而遺傳算法(genetic algorithm，GA)作為一種隨機優化算法，它可以有效地利用已有的信息處理來搜索那些有希望改善質量的串，數學軟件Matlab 可以實現遺傳算法的快速計算和結果分析。

遺傳算法工具箱(gatool)是Matlab 軟件自帶的一個工具箱，為遺傳算法的快速實現提供很大的幫助。gatool 的部分截圖如圖2 所示。

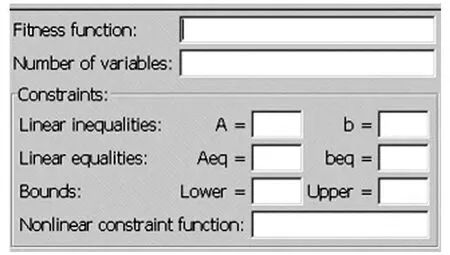
圖2 gatool 部分截圖

Fitness function:適應值函數，即目標函數，根據目標函數，編寫約束條件代碼，以X.m 文件名保存，并在右側空白框中輸入@ X 文件，即適應值函數文件;Number of variables:變量的個數;Constraints:約束條件;Linear inequalities:以Ax≤b形式的線性不等式約束條件，A可以是矩陣也可以是單個數字，b可以是列向量也可以是單個數字;Linear equalities:以Ax=b形式的線性等式約束條件;Bounds:變量的上下限，Lower 為下限，Upper 為上限，二者可以是單個數字也可是向量;Nonlinear constraint function:非線性約束條件，根據實際約束條件，編寫約束條件代碼，以XX. m 文件名保存，并在右側空白框中輸入@XX 文件，即約束條件文件。最后點start(運行)，就得到相應結果。

3 案例分析

現有5 個地址D1—D5作為軍事物流配送中心的備選地址，周圍有10 個倉庫提供軍事物資，有20 個部隊用戶需要軍事物資。根據倉庫至配送中心的年單位運費、倉庫年最大運量、配送中心至用戶的年單位運費、部隊用戶需求量等信息(見表1～3)，選擇合適的地址，確保選址的總費用最低，并且得到倉庫至軍事物流配送中心年運量分配結果，軍事物流配送中心至用戶年運量分配結果，以驗證基于LAP-GA 的多軍事物流配送中心選址模型是否合理。

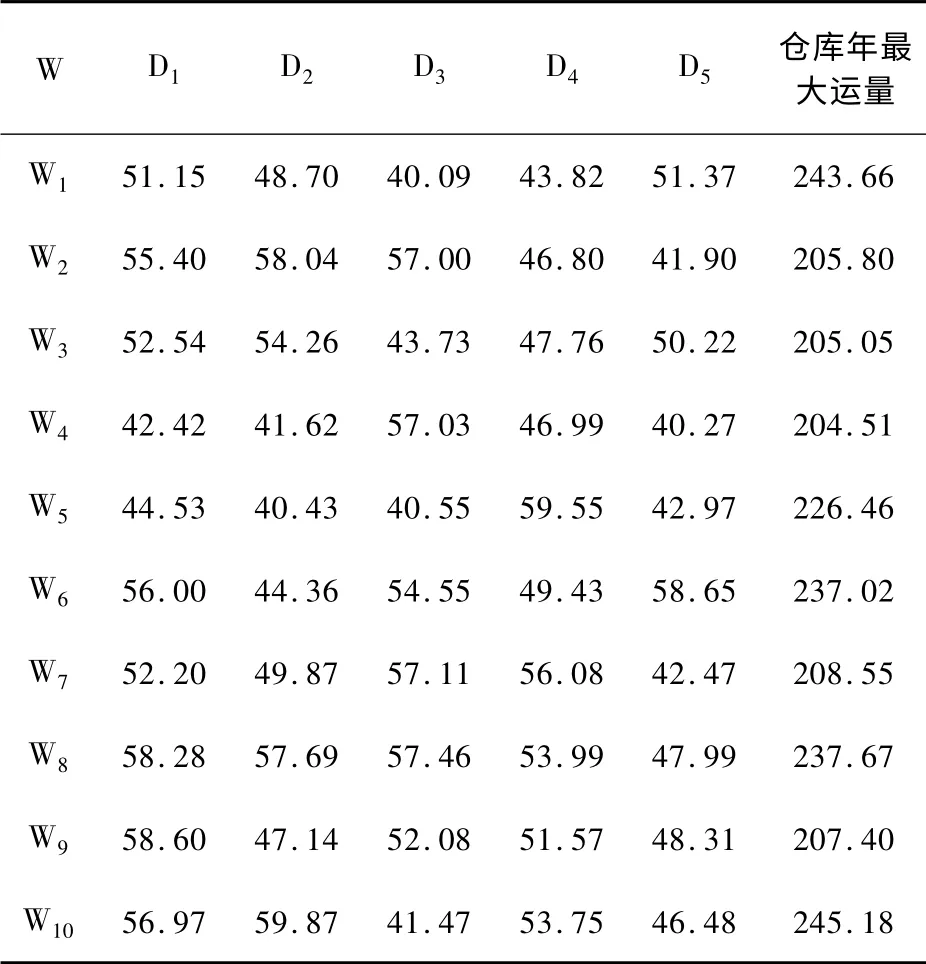
表1 倉庫至配送中心的年單位運費及倉庫年最大運量

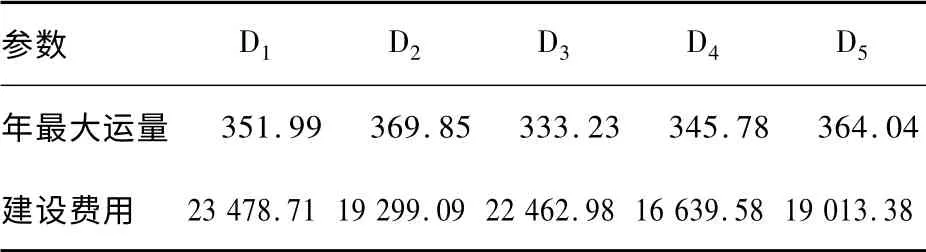
表2 軍事物流配送中心年最大運量和建設費用

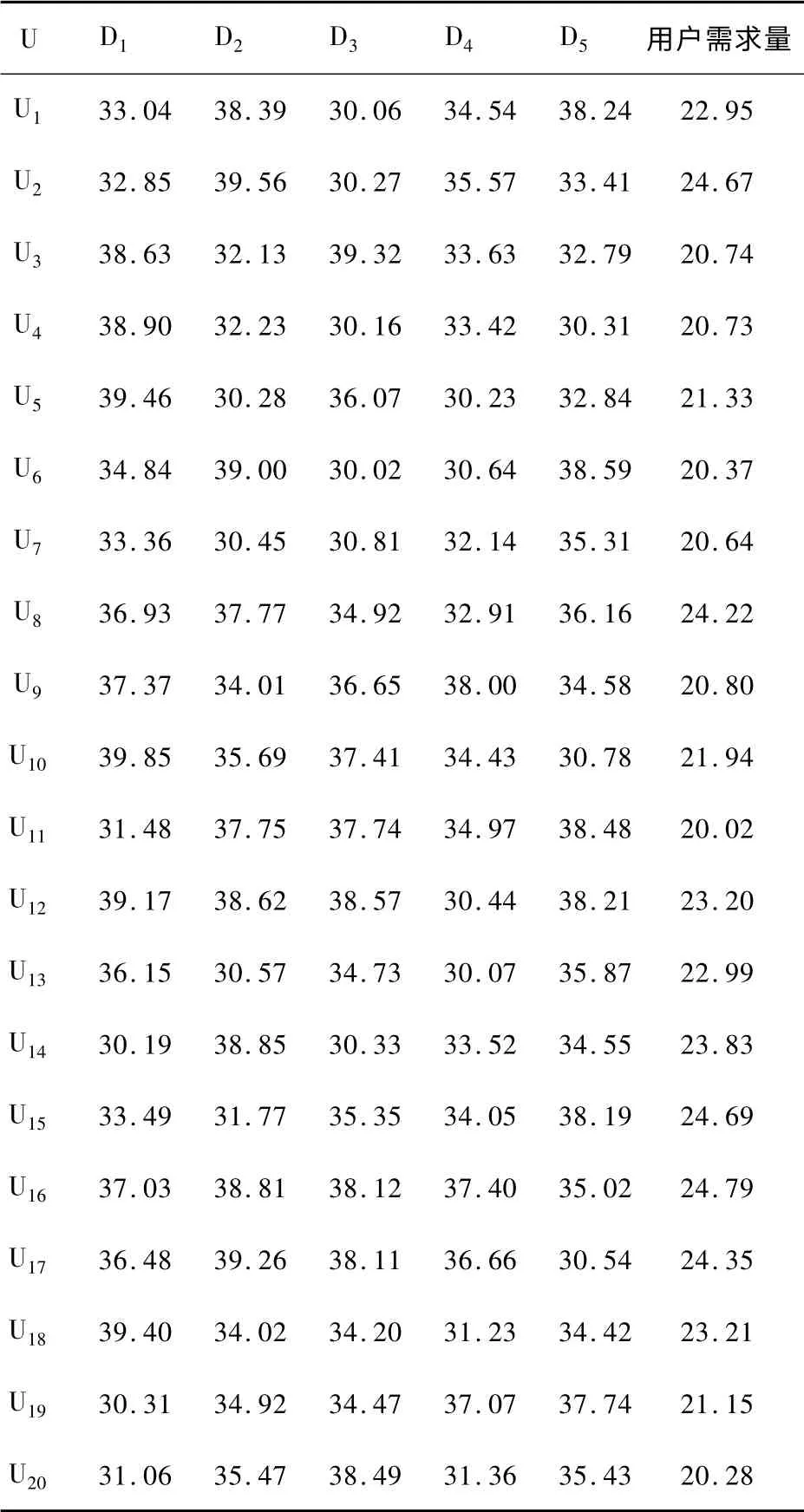
表3 配送中心至用戶的年單位運費及用戶需求量

本案例中共有155 個變量，變量1 ～50 表示10 個倉庫向5 個備選軍事物流配送中心年運量分配;變量51 ～150 表示5 個備選軍事物流配送中心向20 個用戶的年運量分配;變量151 ～155 表示5個備選地址中選擇哪些作為軍事物流配送中心，0表示不選，1 表示選。根據LAP 模型提供的約束條件，用Matlab 語言編寫約束條件代碼并以tcon.m 文件名保存。

按照2.3 介紹的步驟，運行gatool，得到軍事物流配送中心選址結果分析圖(如圖3、圖4 所示)、軍事物流配送中心選址結果(見表4)、倉庫至軍事物流配送中心的年運量分配(見表5)、軍事物流配送中心至用戶的年運量分配(見表6)。

圖3 中，位于下側的點表示每代的最優值，位于上側的點表示每代的平均值，隨著迭代次數的增加，最優點和平均值點就會越接近。當到了第2代以后，最優點和平均值點就非常接近了，到第5代時，最優點和平均值點幾乎重合，迭代結束，說明第5 代是最優秀的子代，此時的最優解就是全局最優解了，即總費用Tc=7.69 ×104。

圖4 中，第5 代最優解中，分別在30 ～40 處和90 ～130 處出現了峰值。30 ～40 處出現峰值表明10 個倉庫向軍事物流配送中心D3和D4運輸軍事物資，90 ～130 處出現了峰值表明軍事物流配送中心D3和D4向20 個部隊用戶配送軍事物資。在變量151 ～155 中，第153、154 變量的值為1，其他為0。因此，選擇備選地址D3和D4作為軍事物流配送中心建設地址。

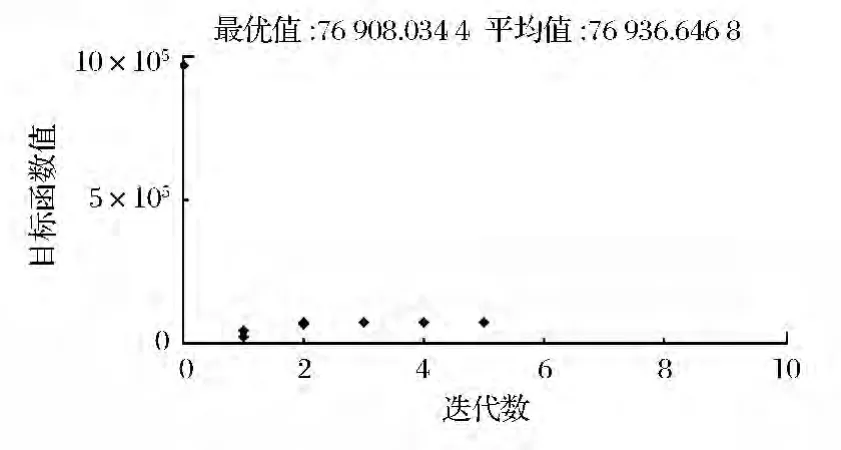
圖3 每代的最優解和平均值

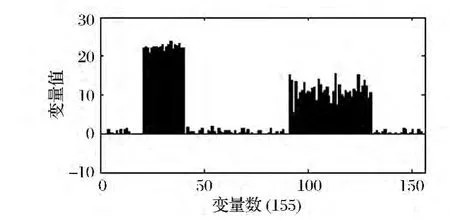
圖4 第5 代最優解

表4 中，軍事物流配送中心選擇第3 和第4 個備選地址作為建設地址。按照表5 和表6 的年運量分配，使多軍事物流配送中心選址總費用最低，總費用Tc=7.69 ×104，其中倉庫至軍事物流配送中心D3、D4的年總運費Wc=2.26 ×104，軍事物流配送中心D3和D4至用戶的年總配送費用Dc=1.52 ×104，軍事物流配送中心D3和D4總建設成本Pc=3.9 ×104。

表4 軍事物流配送中心選址結果

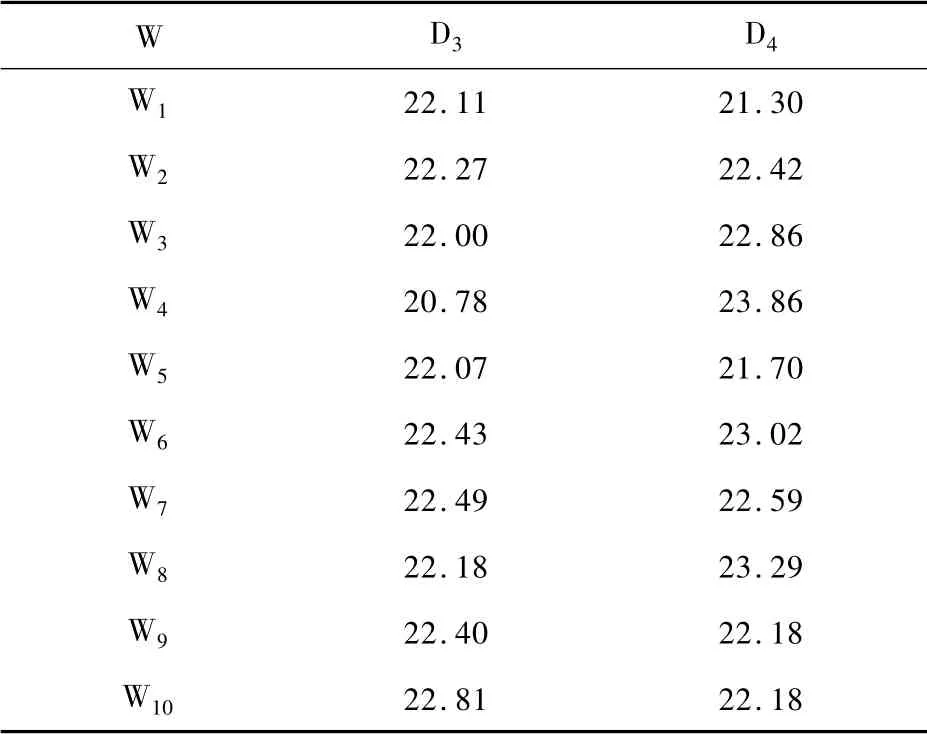
表5 倉庫至軍事物流配送中心年運量分配

表6 軍事物流配送中心至用戶年運量分配

用0—1 規劃得到圖5，此時總配送費用Dc=1.53 ×104，大于用遺傳算法算出的總運費Dc=1.52 ×104，而且用0—1 規劃需要迭代50 次才能得到最優解，遺傳算法只要迭代到5 次就得到最優解，所以用遺傳算法求解LAP 模型既最優又快速。

圖5 0—1 規劃迭代軌跡

4 結 語

本文通過對多軍事物流配送中心選址問題的詳細研究，建立了基于LAP-GA 的多軍事物流配送中心選址模型，并通過Matlab 中的gatool，實現了模型的快速求解和結果分析，節約了軍事物流配送中心建設成本和軍事物流配送費用，為以后的多軍事物流配送中心選址研究提供了借鑒。但本文有些假設趨于理想化和遺傳算法解的過早收斂等問題，是影響選址的重要因素，也是下一步研究的重要內容。

［1］ 王豐，姜大立. 軍事物流學［M］. 北京:中國物資出版社，2004:225-227.

［2］ 胡德全. 軍事物流配送系統研究［D］. 北京:后勤學院，2003:11.

［3］ 肖劍，陳義華.基于遺傳算法的物流中心選址模型及算法研究［D］.重慶:重慶大學，2005.

［4］ 王月玲，薛大伸，趙煥忠.物流配送中心選址策略研究［D］.大連:大連海事大學，2005.

［5］ 高學東，李宗元.物流中心選址模型及一種啟發式算法［J］.運籌與管理，1994，3(3):56-62.