穿浪雙體船T型水翼狀態反饋H∞控制器設計

張松濤，孫明曉，梁利華，姜見龍

(哈爾濱工程大學 自動化學院，黑龍江 哈爾濱150001)

0 引 言

20世紀80年代初期，為了改善雙體船的耐波性，在高速雙體船和小水線面雙體船的基礎上設計了穿浪雙體船(WPC)。該船型繼承了前者低阻、高耐波性等優點，克服了小水線面雙體船的一些缺點，并融合了深V型船優良的航行性能。其適用面廣，載客載貨均可;船體采用鋁合金材料，運用新型設計方式，實現了船舶的輕量化、高速化［1］。

WPC 高速航行時，縱向運動引起的垂向加速度使乘員暈船，設備短期失效，同時會損失航速，使航行效率降低;嚴重時會對船體、貨物和乘員的安全構成極大的威脅。為了有效解決此問題，在船首安裝一個能活動的T型水翼，用來抑制船體的縱向運動，如圖1所示。

T型水翼由支柱和水平翼構成，運用有效的控制策略使水平翼轉動，可以提供恢復力和力矩抵消海浪對船體的擾動力和力矩，以減小船體的縱向運動［2］。文獻［3］運用Fluent 對裝備T型水翼的穿浪雙體船進行耐波性仿真實驗，從理論上分析其良好的效果。文獻［4］將T型水翼安裝在與110 m 實船的比例為1/40的自主動力高速船模上，在露天水域進行航速實驗，證明T型水翼可以減小能量消耗。本文在此基礎上對穿浪雙體船T型水翼的控制系統進行設計。

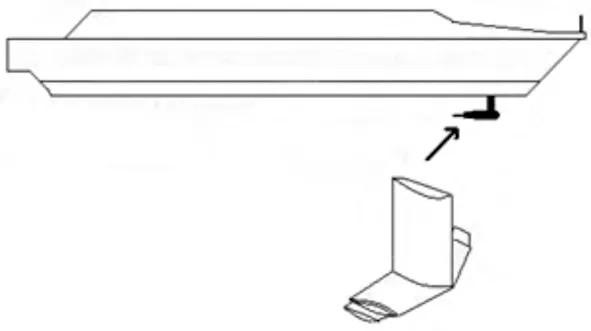
圖1 穿浪雙體船和T型水翼Fig.1 Wave piercing catamaran and T-foil

1 模型分析

1.1 WPC 運動模型

為建立船體運動模型，引入如下假設［5］:

1)假設引起穿浪雙體船運動的入射波的波幅微小，可以認為波浪擾動力微幅，由此假定擾動引起的船體運動也微幅。根據以上假設，可以確定穿浪雙體船的運動方程組是線性的。

2)為了簡化方程中水動力系數的計算，假設水域無限深，且不考慮水域中流和風對船舶運動的影響。

3)假設船體位于水下部分的片體足夠細長，滿足應用切片理論計算運動方程中水動力系數的要求。

根據以上假設條件，穿浪雙體船在波浪中的耦合運動可用如下二階線性常微分方程組表示:

式中:ηk為船舶產生的六自由度運動;為線速度或角速度;為線加速度或角加速度;Mik為船舶質量矩陣;Aik為水的附加質量系數;Bik為水動力阻尼系數;Cik為恢復力系數;為海浪干擾力或力矩的復振幅值;ωe為海浪遭遇頻率，rad/s。下標i = 1～6 同k 一樣，分別代表縱蕩、橫蕩、垂蕩、橫搖、縱搖和首搖六自由度。

由于穿浪雙體船的2個船體形狀相同，且對于縱中剖面對稱，所以船的縱向運動和橫向運動之間無耦合。根據式(1)得到垂蕩和縱搖耦合運動的方程組，即為穿浪雙體船在海浪擾動作用下，縱搖和垂蕩運動模型:

1.2 系統運動模型

建立帶T型水翼穿浪雙體船的運動模型時，將系統模型分為3 部分，如圖2所示:一部分是計算海浪產生的力和力矩，一部分是計算T型水翼產生的力和力矩，一部分是計算由作用于船體的力和力矩產生的船舶垂蕩和縱搖運動。T型水翼可起到平衡海浪對船體擾動，利用翼面所產生的恢復力和力矩與波浪的力和力矩相抵，達到減小垂蕩和縱搖運動幅度的目的。

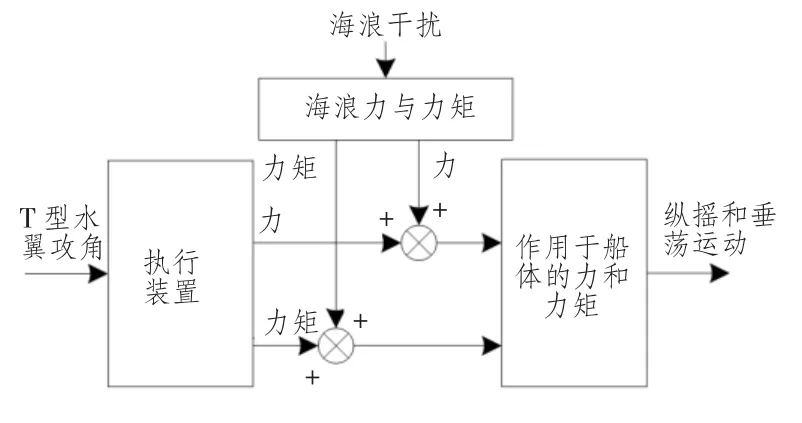
圖2 控制系統圖Fig.2 Control system

帶T型水翼穿浪雙體船縱向運動的線性微分方程:

其相應的狀態空間模型:

式中:

1.3 研究對象

穿浪雙體船具體參數為:船長90 m，排水量740 t，吃水2.6 m。運用切片理論進行計算［6］，垂蕩、縱搖的運動狀態空間參數為:

T型水翼的升力計算模型如下:

式中:ρ為水密度;A為翼面積;U為船速;α為翼面的有效攻角;CL(α)為翼的升力系數，在α 很小的情況下可將其視為常量。

高航速下水翼的效率高，其升力系數受到了諸多因素的影響，如翼與主船體之間的相互耦合，邊界層影和非定常運動效應等。

利用CFD 軟件Fluent 獲得T型水翼在不同來流速度下的升力系數，如圖3所示。根據式(9)計算獲得T型翼在不同攻角下的升力系數，通過擬合的方式得到升力系數滿足的函數Y(x)，如下式:

式中:CL(α)為升力系數;FL為升力;ρ為水密度;U為水流相對于物體的流速;A為水翼面積。

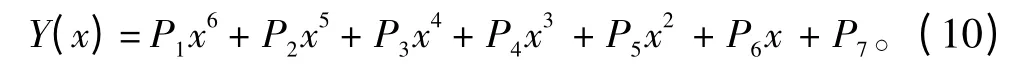
式中:x為攻角;系數P1=－6.6323 ×10－10，P2=8.7419 ×10－9，P3=1.8168 ×10－7，P4=－2.0541 ×10－5，P5=－5.2744 ×10－5，P6=0.066459，P7=－0.0071406。

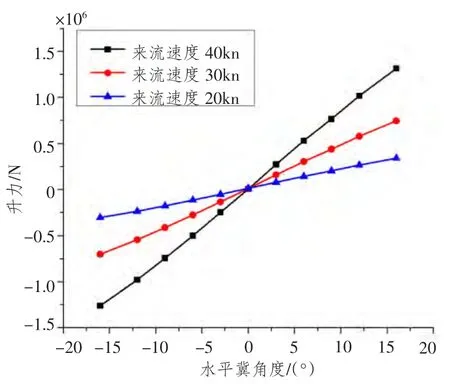
圖3 不同來流速度下的升力Fig.3 Lift under different stream velocity

2 狀態反饋H∞控制策略

為使穿浪雙體船T型水翼系統抵抗隨機海浪的干擾，故需要實用可靠的控制策略，而狀態反饋H∞控制思想可歸結為:在一個具有有限能量的干擾信號作用下，為系統設計控制器，該控制器不僅可以使閉環系統穩定，還可以使干擾對系統期望輸出造成的影響最小［7］，正契合T型水翼控制系統需要。

狀態反饋H ∞控制方法是由Doyle，Glover和Khargonekar 等提出的，是一種設計過程簡單、計算量小的H∞控制器求解方法，可通過求解一個代數Riccati 方程來獲得階次較低，結構特征明顯的控制器。

狀態反饋H∞理論并不屬于標準H∞控制問題，在討論狀態反饋H∞控制問題時，系統的狀態全部可測，觀測量等于狀態變量，即y = x，那么存在廣義對象G(s)的狀態空間實現為:

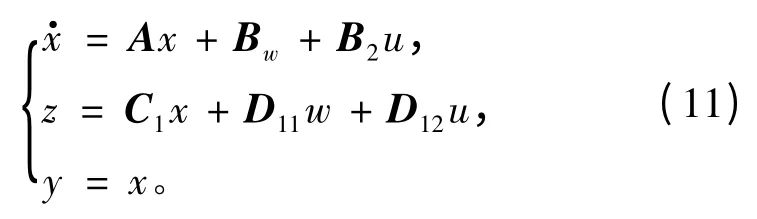
相應的存在:

式中:x為n 維狀態向量;w為m1維干擾輸入向量;u為m2維控制輸入向量;z為p1維受控輸出向量;y為n 維觀測輸出向量;矩陣A ∈Rn×n，B1∈Rn×m，B2∈Rn×m2，C1∈Rp1×n;D11和D12為實數矩陣且它們的維數與其他量的維數相對應。

實際上，可將狀態反饋H∞控制器設計問題看成是線性系統二次型性能指標的最優控制問題，也就是對于系統的線性模型，設計控制器K 使如下性能泛函J為最小:

式中:Q為正定對稱矩陣，即滿足Q = QT＞0;R滿足R ＞0;γ為干擾抑制水準的一個正常數。

假設［A，B2］可控，［A，Q］可觀;系統的觀測量等于狀態變量，即y = x。如果對于所有的γ ＞0使得如下廣義代數黎卡提(Riccati)方程:

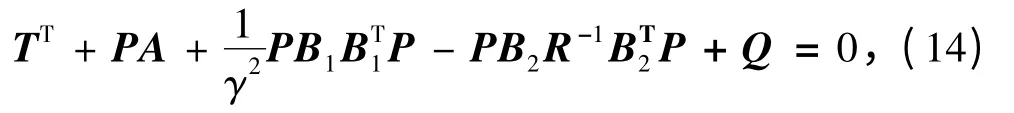
存在正定對稱解陣P = PT≥0，進而可以得到滿足式(14)中性能指標的狀態反饋H∞控制器K，使得u = kx =－R-1BT2Px，即K =－R-1BT2P。

如果式(14)中的H∞性能指標γ →∞，那么該式就成為LQR 最優控制問題中的Riccati 方程，此時H∞控制問題就變成了LQR 問題。狀態反饋H∞控制問題狀態空間模型與LQR控制有所差別，其廣義對象的狀態空間方程為:

其中

式中:w為海浪干擾輸入，w =［FwaveMwave］T;Fwave為海浪產生的垂蕩擾動力;Mwave為海浪產生的縱搖擾動力矩。

可將狀態反饋H∞控制器設計問題看作線性系統二次型性能指標的最優控制問題。

3 控制器設計

在狀態反饋H∞控制器設計過程中，H∞范數指標γ、加權系數或加權系數矩陣都是調試參數，可以通過調整這些參數得到較滿意的控制器設計結果。

雖然H∞范數指標γ和加權系數是可調參數，但不可盲目設定，應結合實際問題來確定。

因此，在一般情況下，考慮γ ≤1 即可設計控制器K，使得閉環系統內部穩定，但是對于本文所研究的系統，利用該指標設計的狀態反饋H∞控制器的控制效果不理想，因此將γ的范圍限制在1以內。

考慮到式(14)中的Q為正定對稱矩陣，且滿足［A，Q］可觀測，并結合遺傳算法對參數進行優化選取，最終選取Q =diag (［17.488，39.042，39.951，38.432］)，R =0.318。選取γ =0.356，經過計算可得狀態反饋增益矩陣:

4 仿真實驗驗證

4.1 實驗方法

在Matlab/SIMULINK 環境中，穿浪雙體船在5級海況，波高3.25 m，迎浪角180°，以40 kn 航速行駛，針對未安裝T型水翼和安裝T型水翼2 種方式［8］。

1)進行船體不同位置暈船率仿真實驗，并統計分析船舶運行2 h 后的暈船率。

舒適度的評價標準是通過計算暈船率(MSI)來分析［9］，計算公式如下:

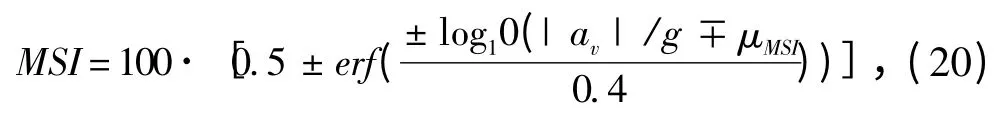
式中:erf為誤差函數;| av|為檢測點的垂直加速度;μMSI為給定的經驗公式。

式中ω為垂直加速度的頻率。

2)對船舶縱搖和垂蕩運動進行仿真實驗，并對比分析實驗結果。

4.2 實驗結果

1)對船體不同位置暈船率統計如表1所示。

表1 船體不同位置暈船率統計Tab.1 MSI of different locations in hull

2)船體的垂蕩和縱搖運動仿真曲線如圖4所示。虛線和實線分別為安裝受控的T型水翼和無T型水翼2 種方式。

圖4 垂蕩、縱搖運動曲線Fig.4 Motion curve of heave and pitch

4.3 結果分析

由表1和圖4 可知:加入受控的T型水翼后，船體的垂蕩位移、垂蕩速度、垂蕩加速度、縱搖角、縱搖速度和縱搖加速度均明顯改善了，垂蕩位移減少了20%，縱搖角減少了43%，隨著時間的推移，效果好于開始狀態，系統穩定性好。垂蕩加速度在多數情況下能夠控制在1 m/s2以內，船體不同位置的暈船率都大幅降低，滿足乘員對垂蕩加速度的要求，提高了乘員的舒適度。

實驗結果表明:利用狀態反饋H∞控制設計控制器，可以有效地控制穿浪雙體船T型水翼的水平翼繞固定軸轉動，利用T型水翼上產生的升力及力矩抵消海浪干擾力及力矩，實現了減小穿浪雙體船的縱向運動的目的。

5 結 語

根據狀態反饋H∞控制策略設計的控制器實現了穿浪雙體船T型水翼的有效控制，減小了船體的縱向運動和垂向加速度，降低了暈船率，驗證了控制器的有效性。

狀態反饋H∞控制方法具有一定的理論和工程實用價值，為廣泛興起的高速船縱向運動過大問題提供了借鑒方法。下一步將優化水翼參數，并探索運用到多水翼的高速船姿態運動控制系統中。

［1］夏齊強，陳志堅，孫春生.鋁合金穿浪雙體船波激振動響應計算研究［J］.艦船科學技術，2010，32(2):11－16.XIA Qi-qiang，CHEN Zhi-jian，SUN Chun-sheng.A study on waveinduced vibration for aluminum alloy wave piercing catamarans［J］.Ship Science and Technology，2010，32(2):11－16.

［2］LIANG Li-hua，WANG Bao-hua，ZHANG Song-tao.Stabilizer fin effect on SWATH ship motions and disturbance observer based control design［C］.2013 10th IEEE International Conference on Mechatronics and Automation，Takamastu，Japan，2013:1147－1152.

［3］LIANG Liang，JIANG Jian-long，ZHANG Song-tao.Improving the vertical motion of wave piercing catamaran using T－foil［C］.2013 IEEE International Conference on Mechatronics and Automation，Takamastu，Japan，2013:1481－1485.

［4］ESTEBAN S，RECAS J，GIRON-SIERRA J M，et al.A fast autonomous scaled ship for experimental seakeeping control studies［C］.Oceans 2005－Europe.IEEE，2005:1232－1237.

［5］FALTINSEN O M，崔維成譯.海上高速船水動力學［M］.北京:國防工業出版社，2007.FALTINSEN O M.Hydrodynamic speed boat at sea［M］.Beijing:Defense Industry Press，2007.

［6］韓曉光，吳晞，鄭環宇.波浪對穿浪雙體船搖蕩運動的影響［J］.艦船科學技術，2012，34(4):13－16.HAN Xiao-guang，WU Xi，ZHENG Huan-yu.Research on wave-piercing catamaran features of swaying motions in the waves［J］.Ship Science and Technology，2010，2012，34(4):13－16.

［7］解學書，鐘宜生.H∞控制理論［M］.北京:清華大學出版社，1994.XIE Xue-shu，ZHONG Yi-sheng.H∞Control Theory［M］.Beijing:Tsinghua University Press，1994.

［8］ZHANG Song-tao，LIANG Li-hua，WANG Jing-fu.Analysis of real time stabilization effect and parameter optimization of fin stabilizer ［C］.2012 9th IEEE International Conference on Mechatronics and Automation，Chengdu，China，2012:1103－1108.

［9］FOSSEN T I.Handbook of marine craft hydrodynamics and motion control［M］.John Wiley ＆ Sons，2011.